 |
§2. Площадь поверхности, заданной параметрическими уравнениями
|
|
|
|
§2. Площадь поверхности, заданной параметрическими уравнениями
Часто поверхности удобно задавать параметрическими уравнениями
,
где 
, а 
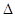- некоторая плоская область, ограниченная кусочно-гладкими кривыми. Пусть 
.
Кроме того, пусть в любой точке 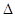ранг матрицы 
равен 2. Это означает, что в любой точке 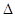хотя бы один из миноров второго порядка этой матрицы не равен 0. Если, скажем, в некоторой точке 
, то это означает (вспомним сформулированную в конце второго семестра теорему о системе неявных функций), что уравнения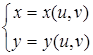 
можно решить, выразив в окрестности этой точки переменные 
через переменные 
, т. е. получить равенства вида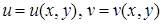 
. Подставив эти выражения в уравнение 
, получим уравнение 
, т. е. в окрестности рассматриваемой точки поверхность может быть задана явным уравнением вида (1).
(Если другой минор, например,
,
то имеем, по аналогии,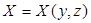 
, а если минор
, то 
).
Обозначим символом 
вектор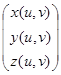 
. Рассмотрим произвольную точку 
. Зафиксируем сначала 
и рассмотрим 
– кривую на поверхности. Тогда
–
вектор касательной к этой кривой. Аналогично,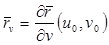 
- вектор касательной к кривой 
.
Нормаль к поверхности является нормалью к касательной плоскости и перпендикулярна 
и 
. Условие
означает, что и не параллельны. Поэтому в качестве нормального вектора можно взять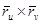 
(векторное произведение) или
.
Тогда единичные векторы нормали равны 
, при этом выбору верхней нормали соответствует выбор того же знака, что и знак числа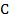 
, перед корнем (поскольку тогда 
).
Если поверхность задана параметрическими уравнениями, то, как указывалось выше, в окрестности любой её точки её возможно задать явным уравнением ( 
, или 
, или 
).
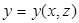Предположим, что поверхность, заданная параметрическими уравнениями, представляет собой объединение конечного числа частей, каждая из которых задана явным уравнением, и рассмотрим одну из её частей, для которой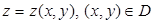 
. Тогда площадь этой части, по доказанному выше, равна 
. Перейдём в этом интеграле к переменным 
, учитывая, что якобиан перехода – это как раз определитель 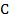, а 
, и пусть области 
соответствует область 
на плоскости 
. Тогда по теореме 1. 5 (о замене переменных в двойном интеграле)
|
|
|
.
Легко проверить, что в случае уравнения или 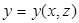получится интеграл такого же вида: 
Объединяя все полученные части, получаем общую площадь 
, где 
‑ вся область изменения параметров 
Отметим, что выражение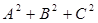 
можно преобразовать к более удобному для вычислений виду.
Числа 
являются координатами вектора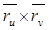 
. Поэтому 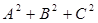– квадрат модуля вектора 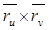. Напомним, что модуль векторного произведения равен 
( 
- угол между 
). Значит, 
.
Введём обозначения
; 
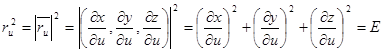и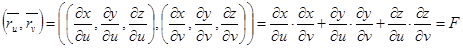 
.
Тогда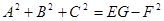 
, и формула для площади поверхности, заданной параметрическими уравнениями, такова: 
.
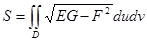§3. Поверхностные интегралы 1-го типа
Пусть 
– поверхность, имеющая площадь 
. Рассмотрим разбиение 
этой поверхности на части Si с помощью непрерывных кусочно-гладких кривых. Пусть функция 
определена во всех точках поверхности S. Выберем произвольным образом точки 
и рассмотрим сумму
.
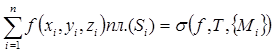Определение. Пусть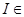 
ℝ. Если 
, то мы говорим, что I есть поверхностный интеграл 1-го типа от функции по поверхности 
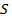и обозначаем это следующим образом: 
.
Пример задачи, моделью которой служит поверхностный интеграл первого типа – нахождение массы поверхности S, поверхностная плотность которой в точке 
равна .
Поверхностный интеграл первого типа обладает свойствами линейности и аддитивности. Для вычисления поверхностного интеграла 1-го типа удобно использовать следующие теоремы.
Теорема 4. 1. Пусть поверхность 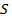задана уравнением 
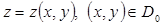, где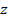 
– непрерывно дифференцируемая на квадрируемой области 
функция,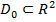 
. Тогда для любой непрерывной на поверхности 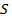функции 
выполнено равенство
|
|
|
|
|
|
