 |
1.2. Критерий интегрируемости. §2. Свойства двойных интегралов
|
|
|
|
1. 2. Критерий интегрируемости
Критерий существования определённого интеграла 
формулировался в терминах сумм Дарбу, т. е. сумм вида 
, 
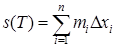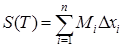, где 
, 
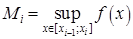, то есть 
- нижняя грань, а 
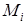- верхняя грань значений 
при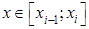 
.
Рассуждая аналогично, рассмотрим для ограниченной на квадрируемом множестве 
функции 
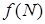числа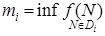 
, 
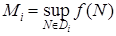(эти числа существуют ввиду предполагаемой ограниченности функции 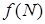на и, значит, на всех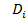 
. Определим суммы Дарбу равенствами 
, 
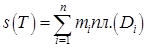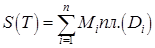. Эти величины представляют собой объемы тел, состоящих из цилиндров с основаниями 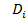и высотами, соответственно, 
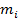и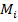 
. Ясно, что для любого разбиения 
при любом выборе точек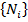 
выполнены неравенства между суммами Дарбу и интегральной суммой, соответствующей этому выбору точек: 
.
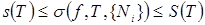На рисунке изображены тела, объёмы которых равны суммам Дарбу.
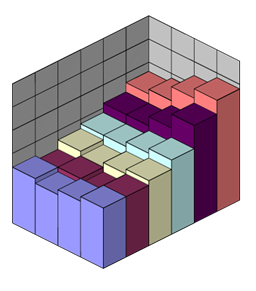Нижняя сумма Дарбу
| 
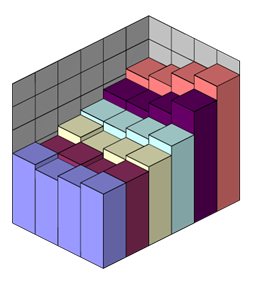Верхняя сумма Дарбу
|
Вполне аналогично одномерному случаю можно доказать критерий существования двойного интеграла.
Теорема 1. 1. Ограниченная на квадрируемом множестве функция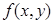 
интегрируема тогда и только тогда, когда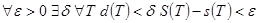 
(На экзамене ограничиваемся формулировкой).
Из этого критерия следует теорема.
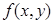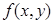Теорема1. 2. Если функция непрерывна на квадрируемом множестве , то интегрируема на этом множестве.
(На экзамене достаточно формулировки).
§2. Свойства двойных интегралов
Свойство 1 . Если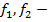 
- интегрируемые на квадрируемом множестве функции, а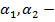 
числа, то
.
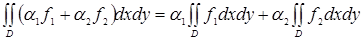Иными словами, интеграл - линейный функционал.
Свойство 2. Если 
- интегрируема на объединении квадрируемых множеств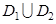 
, то
,
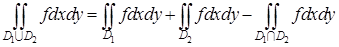причем если площадь пересечения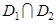 
равна 0, то 
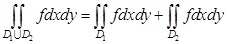. (Аддитивность интеграла по множеству).
Свойство 3. Если - интегрируемая на квадрируемом множестве функция и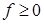 
, то 
.
|
|
|
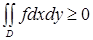Свойство 4. Если 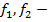- интегрируемые на квадрируемом множестве функции и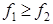 
, то 
.
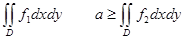Свойство 5. Если - интегрируемая на квадрируемом множестве функция, причем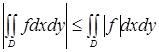 
.
Свойство 6. Если - интегрируемая на квадрируемом множестве функция, то функция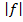 
– также интегрируемая, причем 
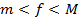где т, М ограничивающие множество значений функции числа, то выполняются неравенства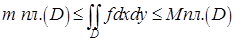 
,
т. е. существует число 
, удовлетворяющее неравенствам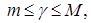 
для которого
.
Если, кроме того, множество – связное* и - непрерывна на нём, то существует точка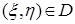 
, для которой
.
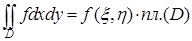Доказывать эти свойства мы не будем, поскольку их доказательства вполне аналогичны доказательствам свойств обычного интеграла.
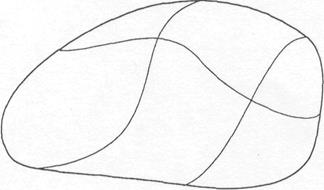
В конце п. 1. 2. отмечено, что если - непрерывная на множестве функция, то - интегрируема на . Свойство 2 позволяет утверждать, что если имеет разрывы на 
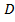лишь вдоль конечного числа спрямляемых линий, разбивающих на квадрируемые области, то - интегрируема на , т. к., по свойству 2, интеграл по есть просто сумма конечного числа интегралов по полученным частям (на которых непрерывна и, значит, интегрируема).
*Примечание. Связным множеством на плоскости назовем такое множество, любые две точки которого можно соединить кусочно-гладкой кривой, лежащей в этом множестве.
3. Вычисление двойного интеграла сведением к повторному интегралу
Двойной интеграл – новый объект и мы укажем способ его вычисления сведением к повторному вычислению определённого интеграла. Сначала рассмотрим двойной интеграл по прямоугольной области 
стороны которой параллельны осям координат.
Теорема 1. 3. Пусть для функции 
существует двойной интеграл 
по области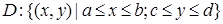 
. Кроме того, пусть для любого 
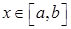существует 
.
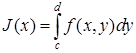Тогда существует и интеграл, называемый повторным:
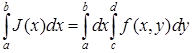
и выполняется равенство
|
|
|
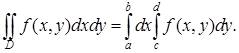(2)
► Разобьём прямоугольник на прямоугольники, обозначенные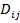 
, прямыми, проходящими параллельно оси 
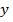через точки 
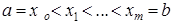и прямыми, параллельными оси 
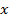и проходящими через точки 
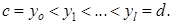Таким образом,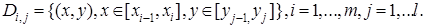 
Пусть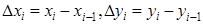 
, числа 
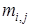и 
, соответственно, равны нижней и верхней граням функции 
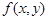на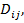 
откуда 
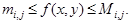Проинтегрируем эти неравенства по 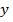на отрезках 
:
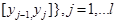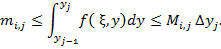
Суммируя эти неравенства по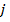 
от 
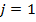до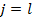 
, получаем
Умножим все части этих неравенств на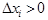 
и суммируем полученные неравенства по 
от 
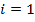до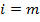 
:
.
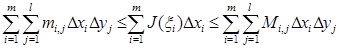Поскольку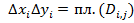 
, эти неравенства можно переписать в виде
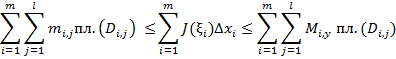
или
,
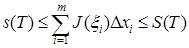где – разбиение на прямоугольники 
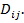При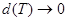 
стремится к нулю и величина 
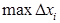. Кроме того, при 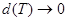также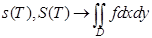 
. Значит, интеграл 
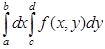существует и равен , что и утверждалось. ◄
|
|
|
