 |
§2. Криволинейные интегралы второго типа
|
|
|
|
§2. Криволинейные интегралы второго типа
Рассмотрим, как и в параграфе 1, кривую 
, которую пока считаем незамкнутой.
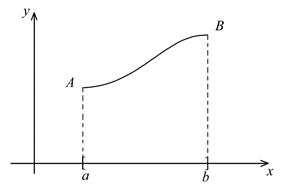
Пусть проекция этой кривой на ось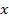 
представляет собой отрезок 
.
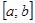Пусть точки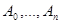 
дают разбиение кривой . Рассмотрим их проекции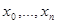 
, лежащие на отрезке 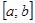и обозначим 
.
Пусть функция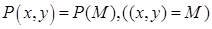 
определена на кривой . Пусть 
- точка, лежащая на кривой между 
и 
. Положим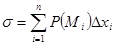 
.
Определение 3. 2. 1. Пусть 
. Если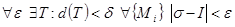 
, то говорят, что I - это криволинейный интеграл второго типа 
.
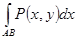Точно также, рассматривая проекции на ось y, определим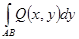 
.
Интеграл общего вида 
определяется, как сумма этих двух интегралов. Он также обладает свойствами линейности и аддитивности.
Вычисление криволинейного интеграла 2-го типа проводится в соответствии со следующей теоремой.
Теорема 3. 2. При условиях предыдущей теоремы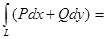 
.
Теорему оставим без доказательства.
Примечание 1.
a) Если кривая L задана явным уравнением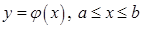 
, где 
- непрерывно дифференцируемая функция, то предыдущая формула принимает вид:
b) Если L задана уравнением 
, то
.
c) Если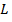 
- отрезок прямой 
, то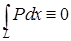 
для любой функции 
, если 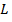- отрезок прямой 
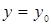, то 
для любой функции Q.
Примечание 2.
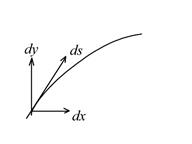
Пусть 
- угол, составляемый вектором касательной к кривой и положительным направлением оси x. Тогда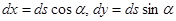 
. Поэтому
.
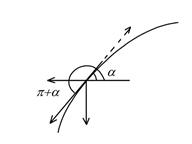
Заметим, что при изменении направления обхода угол изменяется на 
. При этом 
, и интеграл в правой части написанного выше равенства меняет свой знак.
Примечание 3. В случае пространственной кривой L: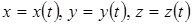 
, где 
- непрерывные на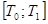 
функции, а f - непрерывна на L, то
.
Аналогично, для непрерывных на L функций P, Q, R имеем
.
Примечание 4. Говорят, что на области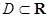 
задано векторное поле 
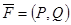, если каждой точке 
сопоставлен вектор 
. Обозначим 
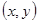- радиус-вектор точки 
и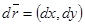 
. Тогда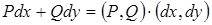 
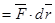(скалярное произведение). Поэтому 
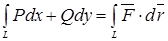. Из физики известно, что эта величина представляет собой работу силы 
вдоль кривой L.
|
|
|
§3. Формула Грина
Эта формула обобщает формулу Ньютона-Лейбница.
Теорема 3. 3 . Пусть 
- криволинейная трапеция: 
, где 
- непрерывно дифференцируемые на 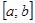функции, 
- граница области и направление обхода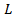 
выбрано так, что область 
остается слева.
Пусть. Тогда.
Знак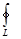 
означает, что контур интегрирования 
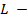замкнутый. Часто используется обозначение 
.
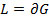► Вычислим двойной интеграл 
, используя теорему Фубини:
.
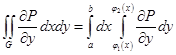При каждом фиксированном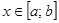 
величина 
определяется, как производная по y функции от одной переменной y, P(x, y). Поэтому при каждом 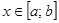применима формула Ньютона-Лейбница, согласно которой
.
Поэтому
.
Разобьем кривую на 4 участка, обозначенные на рисунке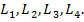 
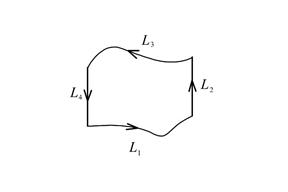
Согласно c) из примечания 1 предыдущего параграфа, 
. По правилу из a) примечания 1,
.
Поэтому
. ◄
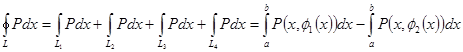
Теорема 3. 4. Пусть - криволинейная трапеция 
, где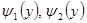 
- непрерывно дифференцируемые на 
функции, граница области и направление обхода 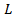выбрано так, что область остается слева.
Пусть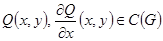 
.
Тогда 
.
► Доказательство повторяет рассуждения предыдущей теоремы.
. ◄
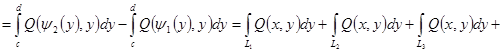
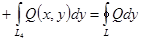Следствие 1. Если область можно представить как в виде криволинейной трапеции 
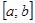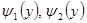, где - непрерывно дифференцируемые на функции, так и в виде трапеции , где - непрерывно дифференцируемые на функции, 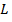– граница области, причем при ее обходе область остается слева, то
.
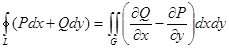Примечание. Области, удовлетворяющие условиям следствия 1 - явление обычное. Например, круг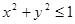 
, ограниченный окружностью 
, можно задать так: 
, а можно и так: 
.
Следствие 2. Если область можно разбить кривыми на конечное число областей, удовлетворяющих условиям следствия 1 и - граница , причем направление обхода выбрано так, что область остается слева, и и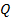 
удовлетворяют перечисленным выше условиям, т. е 
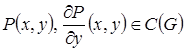и 
, то
|
|
|
|
|
|
