 |
Глава 2. Тройные интегралы. Глава 3.Криволинейные интегралы. §1. Криволинейные интегралы первого типа
|
|
|
|
Глава 2. Тройные интегралы
Рассмотрим кубируемое множество 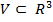 . Считаем, что оно ограничено конечным числом кусочно-гладких поверхностей. Разбиение
. Считаем, что оно ограничено конечным числом кусочно-гладких поверхностей. Разбиение  на части
на части 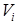 также осуществляется кусочно- гладкими поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции
также осуществляется кусочно- гладкими поверхностями. Диаметр разбиения определяется аналогично двумерному случаю. Также, по аналогии, можно определить для функции 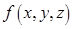 , разбиения
, разбиения  множества
множества  на части
на части 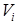 и для выбранных точек
и для выбранных точек 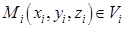 интегральную сумму
интегральную сумму
 ,
,
где  обозначает объем части
обозначает объем части 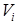 .
.
Определение. Пусть  такое число, что
такое число, что 


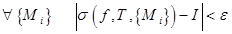 .
.
Тогда мы говорим, что функция  интегрируема на множестве
интегрируема на множестве  , число
, число  есть интеграл функции
есть интеграл функции  по множеству
по множеству  и обозначаем это так:
и обозначаем это так:  .
.
Как и в случае двойного интеграла, выполняются свойства 1-6. Полезное упражнение - переформулировать их для тройного интеграла.
Теорема 2. 1. Ограниченная на кубируемом множестве  функция
функция  интегрируема тогда и только тогда, когда
интегрируема тогда и только тогда, когда 
(На экзамене ограничиваемся формулировкой).
Из этого критерия следует теорема.
Теорема 2. 2. Если функция  непрерывна на кубируемом множестве
непрерывна на кубируемом множестве  , то
, то 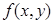 интегрируема на этом множестве.
интегрируема на этом множестве.
(На экзамене достаточно формулировки).
Точно также можно убедиться в том, что если точки разрыва  лежат на конечном числе кусочно-гладких поверхностей, лежащих на
лежат на конечном числе кусочно-гладких поверхностей, лежащих на  и разбивающих
и разбивающих  на кубируемые области, то
на кубируемые области, то  интегрируема на
интегрируема на  .
.
Вычисление тройного интеграла производится по следующему правилу.
Теорема 2. 3. Пусть  задана следующими неравенствами:
задана следующими неравенствами:
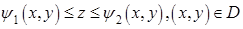 ,
,
где  — квадрируемая область на плоскости,
— квадрируемая область на плоскости,  непрерывные функции. Тогда
непрерывные функции. Тогда
.
Замечание. Если область  задана неравенствами
задана неравенствами  , где
, где  — непрерывные функции, то
— непрерывные функции, то
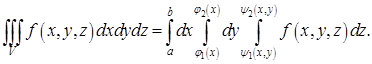
Сформулируем общую теорему о замене переменных.
Теорема 2. 4. Пусть отображение  устанавливает взаимно однозначное соответствие между областями
устанавливает взаимно однозначное соответствие между областями  и
и  , причем функции
, причем функции  — непрерывно дифференцируемые и ни в одной точке
— непрерывно дифференцируемые и ни в одной точке  . Пусть всюду в области
. Пусть всюду в области 
|
|
|
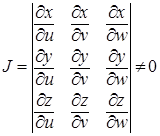
Пусть 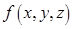 — непрерывная функция. Тогда
— непрерывная функция. Тогда
.
Как и для двойного интеграла, теорема остается верной в случае нарушения ее условий на множестве нулевого объема.
Пример 1. Переход к цилиндрическим координатам. Он осуществляется с помощью функций:  .
.
При этом якобиан равен
 .
.
Пример 2. Переход к сферическим координатам осуществляется функциями  .
.
Якобиан преобразования равен

(разложение определителя по 3-й строке) 
(выделение общих множителей у столбцов)

 .
.
Часто используется интеграл (вы встретите его при вычислении двойных, тройных интегралов при переходе к сферическим или цилиндрическим координатам)
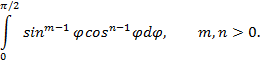
Сведем его к значениям эйлеровых интегралов см. приложение 3:

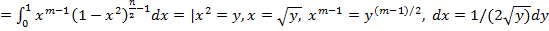 |=
|=

Глава 3. Криволинейные интегралы
§1. Криволинейные интегралы первого типа
Рассмотрим спрямляемую (т. е. имеющую длину) кривую  на плоскости (
на плоскости (  – точки плоскости). Для простоты, считаем, что эта кривая задана параметрическими уравнениями
– точки плоскости). Для простоты, считаем, что эта кривая задана параметрическими уравнениями  , причем
, причем  – непрерывно дифференцируемые на отрезке функции такие, что каждому значению параметра соответствует единственная точка кривой.
– непрерывно дифференцируемые на отрезке функции такие, что каждому значению параметра соответствует единственная точка кривой.
Тогда длина кривой выражается формулой
 .
.
Под разбиением  кривой
кривой  будем понимать множество точек
будем понимать множество точек 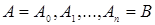 , лежащих на этой кривой и занумерованных в направлении от
, лежащих на этой кривой и занумерованных в направлении от  к
к  . Пусть
. Пусть  - длина кривой
- длина кривой 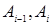 .
.
Диаметр  определим как
определим как  .
.
Пусть функция  определена на кривой
определена на кривой  . Выберем на каждом участке
. Выберем на каждом участке  кривой точку
кривой точку  и образуем сумму
и образуем сумму 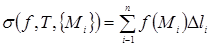 , называемую интегральной.
, называемую интегральной.
Определение 3. 1. 1. Пусть  . Если
. Если 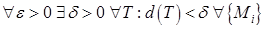
 ,
,
то величина I называется криволинейным интегралом первого типа по кривой  и обозначается так:
и обозначается так:  .
.
Важное замечание. Если бы мы совершали движение по кривой не от  к
к  ,
,
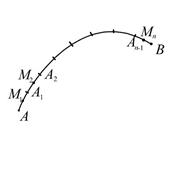
а от  к к  , то в разбиении , то в разбиении  с выбранными точками с выбранными точками  изменилась бы только нумерация отрезков и точек изменилась бы только нумерация отрезков и точек  , а сама интегральная сумма не изменилась бы, поскольку в ее определении фигурирует лишь длина , а сама интегральная сумма не изменилась бы, поскольку в ее определении фигурирует лишь длина  участка, которая не зависит от того, в каком направлении проходится участок. Это означает, что участка, которая не зависит от того, в каком направлении проходится участок. Это означает, что  . .
|
В этом важнейшее отличие от обычного определенного интеграла, который меняет знак при изменении пределов интегрирования (  ).
).
|
|
|
Сформулируем теорему, сводящую новый объект - криволинейный интеграл к обычному определенному интегралу. Определим вспомогательное понятие непрерывности функции на кривой.
Будем говорить, что 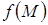 - непрерывная на кривой
- непрерывная на кривой  функция , если
функция , если  (
( 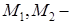 точки кривой такие, что расстояние между
точки кривой такие, что расстояние между  меньше
меньше  ) выполняется неравенство
) выполняется неравенство 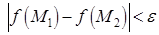 .
.
Теорема 3. 1. Пусть 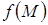 - непрерывная на кривой
- непрерывная на кривой  функция и пусть кривая
функция и пусть кривая  задана параметрическими уравнениями
задана параметрическими уравнениями 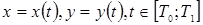 , где
, где 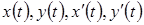 - непрерывные на
- непрерывные на 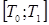 функции, причем каждому значению параметра соответствует единственная точка кривой. Тогда
функции, причем каждому значению параметра соответствует единственная точка кривой. Тогда
 .
.
► Схема доказательства. Интегральная сумма

для криволинейного интеграла первого типа отличается от интегральной суммы 
для интеграла
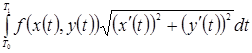
лишь тем, что величина

несколько отличается от величины
 .
.
А именно, этот интеграл, по теореме о среднем, равен
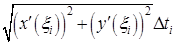 , где
, где  .
.
Нетрудно доказать, что при 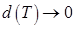 пределы этих сумм равны (строгое доказательство опущено). Это означает, что утверждение теоремы справедливо. ◄
пределы этих сумм равны (строгое доказательство опущено). Это означает, что утверждение теоремы справедливо. ◄
Замечание. Иногда возникает сомнение: мы выразили криволинейный интеграл первого типа, который не меняет свой знак при изменении направления обхода кривой с помощью обычного интеграла, который должен менять знак при изменении пределов интегрирования? Отметим, что изменение направления обхода кривой означает одновременную смену пределов интегрирования и знака величины dt, что не изменяет величину интеграла в правой части этого равенства.
Из свойств криволинейного интеграла отметим следующие 2 основных:
-

при условии, что существуют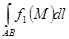 и
и 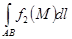 .
. - Если
 - кривые, удовлетворяющие условиям теоремы, то
- кривые, удовлетворяющие условиям теоремы, то  .
.
Эти свойства называются линейностью и аддитивностью интеграла.
Свойство 2 позволяет определить криволинейные интегралы 1-го типа для кусочно-гладких кривых (т. е. кривых, состоящих из конечного числа частей, каждая из которых удовлетворяет условиям теоремы). В частности, можно определить криволинейный интеграл и для замкнутых кривых.
|
|
|
|
|
|


