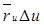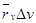|
Замечания.. §4. Замена переменных в двойном интеграле
|
|
|
|
Замечания.
- В случае, когда
 непрерывна на
непрерывна на 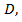 все условия теоремы выполняются и равенство (2) справедливо.
все условия теоремы выполняются и равенство (2) справедливо. - Отметим, что интеграл
 представляет собой собственный интеграл, зависящий от параметра.
представляет собой собственный интеграл, зависящий от параметра.
Рассмотрим случай криволинейной трапеции. Справедлива такая теорема:
Теорема 1. 4 (Фубини). Пусть область  задана неравенствами
задана неравенствами 
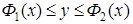 , где
, где  . Пусть существует
. Пусть существует 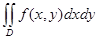 и для любого
и для любого  существует
существует  . Тогда существует интеграл
. Тогда существует интеграл 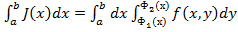 и он равен
и он равен  .
.
► Так как  непрерывна на
непрерывна на  , существует её минимальное значение
, существует её минимальное значение  на этом отрезке. Аналогично, существует максимальное значение
на этом отрезке. Аналогично, существует максимальное значение  функции
функции  на отрезке
на отрезке 
 в прямоугольник
в прямоугольник 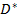 , состоящий из точек
, состоящий из точек  ,
,  ,
, 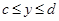 . На этом прямоугольнике рассмотрим функцию
. На этом прямоугольнике рассмотрим функцию
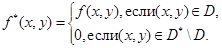
Условия предыдущей теоремы для функции  выполнены. Она интегрируема в
выполнены. Она интегрируема в  , равна 0 (и, значит, интегрируема) в
, равна 0 (и, значит, интегрируема) в  . Следовательно, она интегрируема на всём множестве
. Следовательно, она интегрируема на всём множестве 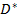 . При этом
. При этом
 .
.
Наконец, для любого 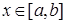 выполнено равенство
выполнено равенство
 .
.
По доказанному в предыдущей теореме,
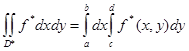 ,
,
откуда сразу получаем:
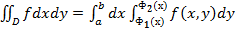 ,
,
что и требовалось доказать. ◄
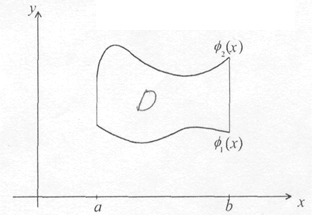
Следствие : Пусть 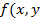 ) непрерывна в области
) непрерывна в области  , ограниченной сверху графиком функции
, ограниченной сверху графиком функции  , снизу -
, снизу -  , где
, где  , a по бокам - отрезками вертикальных прямых х = а и х = b. Тогда
, a по бокам - отрезками вертикальных прямых х = а и х = b. Тогда
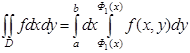 .
.
► Из непрерывности 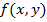 сразу следует её интегрируемость на
сразу следует её интегрируемость на  . Кроме того, для любого
. Кроме того, для любого 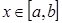 функция
функция 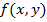 непрерывна (а, значит, интегрируема по у). Все условия теоремы выполнены. ◄
непрерывна (а, значит, интегрируема по у). Все условия теоремы выполнены. ◄
Замечание. Если область  можно ограничить так:
можно ограничить так:

 ,
,  , то
, то
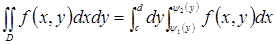 .
.
Смысл этих теорем ясен – указан способ сведения двойного интеграла к собственным интегралам, зависящим от параметра.
§4. Замена переменных в двойном интеграле
При вычислении интегралов часто бывает удобно сделать замену переменных  , где
, где  – непрерывны в некоторой области
– непрерывны в некоторой области 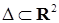 . Впоследствии мы будем часто писать просто
. Впоследствии мы будем часто писать просто 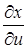 вместо
вместо  и т. п. и, кроме того, говорить при выполнении вышеупомянутых условий, что x и y – непрерывно дифференцируемые в Δ функции. Будем также использовать обозначения
и т. п. и, кроме того, говорить при выполнении вышеупомянутых условий, что x и y – непрерывно дифференцируемые в Δ функции. Будем также использовать обозначения
|
|
|
 .
.
Пусть при этом формулы  задают взаимно-однозначное отображение квадрируемых областей:
задают взаимно-однозначное отображение квадрируемых областей: 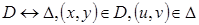 . Кроме того, потребуем, чтобы всюду на области Δ не равнялся 0 якобиан отображения
. Кроме того, потребуем, чтобы всюду на области Δ не равнялся 0 якобиан отображения
 .
.
Теорема 1. 5. При сформулированных выше условиях для непрерывной на 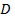 функции
функции 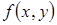 выполняется равенство
выполняется равенство
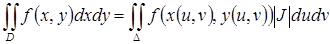 .
.
► Строгое доказательство этой теоремы потребовало бы значительных усилий из-за обилия технических деталей. Мы изложим здесь схему доказательства. Во-первых, оба интеграла в формулировке теоремы существуют, поскольку 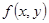 – непрерывная функция.
– непрерывная функция.
| |

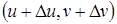



| |
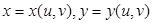 эти точки перейдут, соответственно, в точки
эти точки перейдут, соответственно, в точки 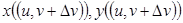
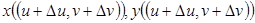

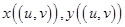
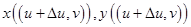
Далее, при 
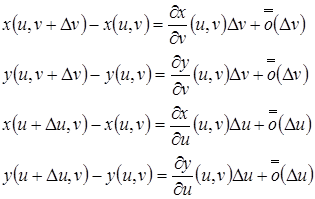

При малых  производные
производные 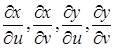 , вычисленные в точках
, вычисленные в точках  , мало отличаются от соответствующих производных, вычисленных в точке
, мало отличаются от соответствующих производных, вычисленных в точке  , поэтому и определённые выше векторы
, поэтому и определённые выше векторы  мало отличаются от векторов
мало отличаются от векторов 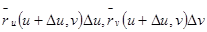 и
и 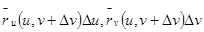 , соответственно, и рассматриваемый четырёхугольник представляет собой «почти параллелограмм».
, соответственно, и рассматриваемый четырёхугольник представляет собой «почти параллелограмм».
Как известно из курса линейной алгебры, площадь параллелограмма со сторонами 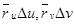
|

равна модулю определителя, составленного из координат этих векторов,
 ,
,
т. е равна 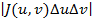 . Поэтому при сделанном преобразовании координат интегральная сумма
. Поэтому при сделанном преобразовании координат интегральная сумма
|
|
|

близка по величине к интегральной сумме
 .
.
Точнее говоря, можно доказать, что соответствующие интегральные суммы для интегралов, стоящих в правой и левой частях доказываемого равенства, отличаются друг от друга на стремящуюся к нулю величину. Поэтому и интегралы совпадают. ◄
Замечание. Утверждение теоремы сохранится, если условие взаимной однозначности отображения  нарушится на множестве нулевой площади.
нарушится на множестве нулевой площади.
§5. Переход к полярным координатам. Вычисление 
Пусть требуется вычислить  по области
по области  , которая задаётся в полярных координатах условиями
, которая задаётся в полярных координатах условиями

Сделаем замену переменных

При этой замене нарушается взаимная однозначность отображения. Точке (0, 0) соответствует целый отрезок 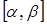 на оси
на оси  . Однако и точка, и отрезок имеет нулевую площадь, и теорема, с учётом замечания, справедлива. Осталось вычислить якобиан преобразования.
. Однако и точка, и отрезок имеет нулевую площадь, и теорема, с учётом замечания, справедлива. Осталось вычислить якобиан преобразования.
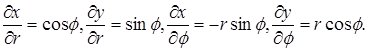

Следовательно,
 .
.
Полярные координаты бывают очень полезны при вычислениях. Рассмотрим пример.
Пример. Найти 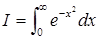 .
.
Решение.  — это несобственный интеграл, и прежде всего следует установить его сходимость. По определению,
— это несобственный интеграл, и прежде всего следует установить его сходимость. По определению,
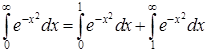 .
.
Первый из интегралов — собственный, второй — сходится по 1-й теореме о сравнении, так как при 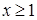 справедливо неравенство, из которого следует, что
справедливо неравенство, из которого следует, что 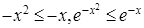 , а интеграл
, а интеграл 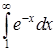 , очевидно, сходится.
, очевидно, сходится.
Обозначим  (очевидно,
(очевидно,  ). Тогда, поскольку обозначение переменной интегрирования можно выбрать произвольным, т. е.
). Тогда, поскольку обозначение переменной интегрирования можно выбрать произвольным, т. е.
 ,
,
имеем
 ,
,
где  — квадрат, а
— квадрат, а  — четверти круга, соответственно, радиусов
— четверти круга, соответственно, радиусов 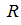 и
и  . Так как
. Так как  , то по свойствам 2, 3 двойного интеграла
, то по свойствам 2, 3 двойного интеграла
 .
.
В интеграле  перейдем к полярным координатам:
перейдем к полярным координатам:
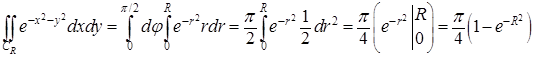 .
.
Аналогично,

и  .
.
При стремлении  к
к  получаем, что
получаем, что
 , то есть
, то есть 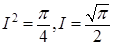 .
.
|
|
|