 |
§4. Поверхностные интегралы 2-го типа
|
|
|
|
.
Замечание 1. Если поверхность задана уравнением  , где
, где 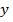 – непрерывно дифференцируемая на квадрируемой области
– непрерывно дифференцируемая на квадрируемой области 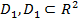 функция, то
функция, то
 .
.
Аналогично, в случае задания поверхности уравнением 

при аналогичных условиях на область  и функцию
и функцию  .
.
Теорема 4. 2. Если поверхность 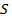 задана параметрическими уравнениями
задана параметрическими уравнениями
 ,
,
где  – непрерывно дифференцируемые функции на квадрируемом множестве
– непрерывно дифференцируемые функции на квадрируемом множестве 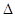 и если функция
и если функция  непрерывна на
непрерывна на  , то
, то
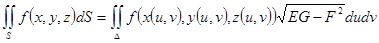 .
.
Теоремы 1 и 2 оставим без доказательства. Вместо этого приведём пример вычисления поверхностного интеграла 1-го типа.
Задача. Найти  , где
, где  – граница тела, координаты точек которого удовлетворяют неравенствам
– граница тела, координаты точек которого удовлетворяют неравенствам 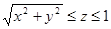 .
.
Решение. Это тело представляет собой конус:

 состоит из боковой поверхности
состоит из боковой поверхности  и основания
и основания 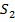 . На боковой поверхности, уравнение которой имеет вид:
. На боковой поверхности, уравнение которой имеет вид: 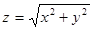 , всюду, кроме точки
, всюду, кроме точки  выполнены равенства
выполнены равенства
 и
и
 .
.
Поэтому
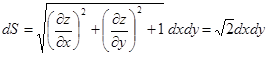 .
.
Нарушение этой формулы в единственной точке  не повлияет на результат вычисления, поэтому
не повлияет на результат вычисления, поэтому 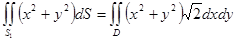 , где
, где  – проекция
– проекция  на плоскость
на плоскость  , т. е.
, т. е. 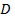 – круг, координаты точек которого удовлетворяют неравенству
– круг, координаты точек которого удовлетворяют неравенству  .
.
В интеграле, стоящем в правой части, перейдём к полярным координатам, (см. §5 главы 1,  якобиан преобразования):
якобиан преобразования):
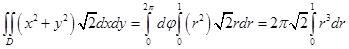
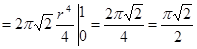 .
.
Основание  задано уравнением
задано уравнением  , поэтому
, поэтому  и
и

(этот интеграл отличается от вычисленного выше лишь множителем, поэтому подробное вычисление опущено).
Итак, весь интеграл равен

§4. Поверхностные интегралы 2-го типа
4. 1. Понятие стороны поверхности
Понятие стороны поверхности интуитивно хорошо известно. Мы говорим о верхней и нижней стороне, внутренней и внешней стороне (для замкнутых поверхностей) и т. п. Однако что такое сторона поверхности и у всякой ли поверхности есть стороны – вопрос, требующий изучения.
|
|
|
Как обычно, проще всего обстоит дело с поверхностью, заданной явным уравнением.

 |
В этом случае, очевидно, есть 2 стороны, верхняя и нижняя. Чтобы определить сторону, достаточно установить, какой угол составляет выбранная Вами нормаль к поверхности с осью
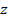 . Если
. Если 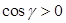 , то это – верхняя сторона поверхности, поэтому ей соответствует единичный вектор нормали
, то это – верхняя сторона поверхности, поэтому ей соответствует единичный вектор нормали

Если 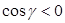 , то это – нижняя сторона поверхности и ей соответствует единичный вектор нормали
, то это – нижняя сторона поверхности и ей соответствует единичный вектор нормали
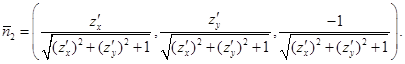
Пусть 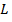 – замкнутый контур, лежащий на поверхности и не пересекающий её край. Выберем в произвольной точке этого контура одно из двух направлений нормали. Пусть при обходе этого контура нормаль меняется непрерывно. Тогда в исходную точку мы вернёмся с исходным направлением нормали.
– замкнутый контур, лежащий на поверхности и не пересекающий её край. Выберем в произвольной точке этого контура одно из двух направлений нормали. Пусть при обходе этого контура нормаль меняется непрерывно. Тогда в исходную точку мы вернёмся с исходным направлением нормали.


Описанное выше свойство поверхности (1) будем считать определением двусторонней поверхности (в общем случае, а не только для поверхностей вида (1)). Бывают поверхности, не являющиеся двусторонними. Простейший пример – лист Мёбиуса. Он получается так:
рассмотрим прямоугольник 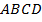 и линию
и линию 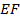 , соединяющую середины его сторон.
, соединяющую середины его сторон.
Склеим точку  с точкой
с точкой 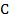 , точку
, точку  с точкой
с точкой  .
.
 Если обходить контур
Если обходить контур 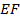 , начиная, например, с точки
, начиная, например, с точки 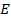 , то при завершении обхода направление нормали непрерывно перейдёт в противоположное. Это доказывает, что лист Мёбиуса не является двусторонней поверхностью.
, то при завершении обхода направление нормали непрерывно перейдёт в противоположное. Это доказывает, что лист Мёбиуса не является двусторонней поверхностью.
В дальнейшем мы будем рассматривать только двусторонние поверхности.
4. 2. Поверхностные интегралы 2-го типа
Пусть 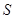 — двусторонняя поверхность. Вначале считаем, что она задана уравнением
— двусторонняя поверхность. Вначале считаем, что она задана уравнением  , где
, где 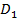 — квадрируемое множество на плоскости
— квадрируемое множество на плоскости  . Как обычно, считаем, что
. Как обычно, считаем, что  — непрерывные на
— непрерывные на 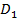 функции, и выберем верхнюю нормаль к поверхности
функции, и выберем верхнюю нормаль к поверхности 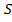 .
.
|
|
|
Разобьем область 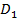 на квадрируемые участки
на квадрируемые участки 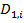 и выберем точки
и выберем точки  произвольным образом. Пусть функция
произвольным образом. Пусть функция 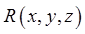 определена на поверхности
определена на поверхности  .
.
Рассмотрим интегральную сумму
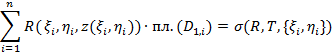
Если  ,
,
то число  называется поверхностным интегралом 2-го типа от функции
называется поверхностным интегралом 2-го типа от функции  по внешней стороне поверхности
по внешней стороне поверхности  и обозначается так:
и обозначается так:  .
.
( Иногда используется обозначение  . )
. )
Если выбрана нижняя сторона поверхности  , то все величины
, то все величины 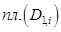 в интегральной сумме заменяем на
в интегральной сумме заменяем на  . Это означает, что поверхностный интеграл II типа (II рода) по нижней стороне поверхности отличается от интеграла по верхней стороне поверхности только знаком.
. Это означает, что поверхностный интеграл II типа (II рода) по нижней стороне поверхности отличается от интеграла по верхней стороне поверхности только знаком.
Подобно тому, как это было сделано в примечании 2 к теореме 3. 2, выразим поверхностный интеграл второго типа через соответствующий интеграл первого типа. Как отмечалось выше,
 , откуда
, откуда 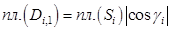 , т. е.
, т. е.
 , если
, если 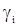 составляет с осью
составляет с осью 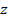 острый угол,
острый угол,
 , если
, если 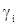 составляет с осью
составляет с осью 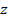 тупой угол.
тупой угол.
Поэтому при любом выборе стороны поверхности имеет место равенство:
 .
.
Таким образом, если  — непрерывная функция, то
— непрерывная функция, то
 , если взята верхняя сторона
, если взята верхняя сторона  и
и
 , если взята нижняя сторона
, если взята нижняя сторона 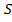 .
.
Если  задана уравнением
задана уравнением  ,
, 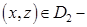 квадрируемой области плоскости
квадрируемой области плоскости  и если
и если 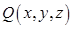 — непрерывная функция, то определён интеграл
— непрерывная функция, то определён интеграл 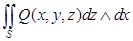 , равный
, равный  и вычисляемый по формуле
и вычисляемый по формуле
 ,
,
если угол, составляемый нормалью к выбранной стороне поверхности с осью 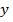 острый, и по формуле
острый, и по формуле
 ,
,
если этот угол тупой.
Если  задана уравнением
задана уравнением  ,
,  квадрируемой области плоскости
квадрируемой области плоскости 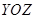 и если
и если  — непрерывная функция, то определён интеграл
— непрерывная функция, то определён интеграл 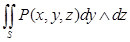 , равный
, равный  и вычисляемый по формуле
и вычисляемый по формуле
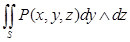
 ,
,
если угол, составляемый нормалью к выбранной стороне поверхности с осью  острый, и по формуле
острый, и по формуле
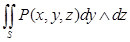
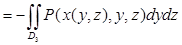 ,
,
если этот угол тупой.
Если поверхность  можно одновременно представить уравнениями рассмотренных выше типов, то определён интеграл общего вида
можно одновременно представить уравнениями рассмотренных выше типов, то определён интеграл общего вида  .
.
Если поверхность  есть конечное объединение таких поверхностей и ориентации этих поверхностей согласованы, то интеграл по всей поверхности равен сумме интегралов по составляющим эту поверхность частям.
есть конечное объединение таких поверхностей и ориентации этих поверхностей согласованы, то интеграл по всей поверхности равен сумме интегралов по составляющим эту поверхность частям.
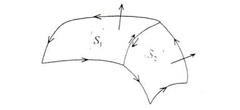
Согласованность ориентации частей поверхности означает следующее: нормали на отдельных частях этой поверхности выбраны так, что положительные направления обхода их общих границ противоположны друг другу.
В общем случае, если поверхность  задана параметрическими уравнениями:
задана параметрическими уравнениями:
|
|
|



где  - квадрируемой области и
- квадрируемой области и 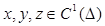 , то
, то

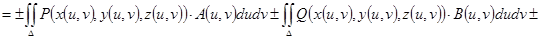
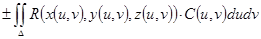
где, как и выше в §2 этой главы, использованы обозначения
 ,
, 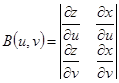 ,
,  ,
,
(то есть эти величины - координаты нормали, равной 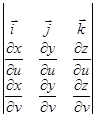 ),
),
а знак “+” или “− ”, стоящий перед ними, выбирается в соответствии с выбором стороны поверхности.
Пример. Приведём примервычисления поверхностного интеграла 2-го типа 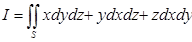 ,
,
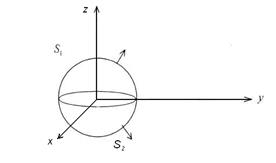
где  – внешняя сторона сферы
– внешняя сторона сферы  . Обозначим
. Обозначим  . Из соображений симметрии очевидны равенства
. Из соображений симметрии очевидны равенства  , так что
, так что  Поверхность
Поверхность  состоит из частей
состоит из частей  и
и 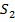 , задаваемых уравнениями
, задаваемых уравнениями  (это
(это  – верхняя полусфера) и
– верхняя полусфера) и  (это уравнение для нижней полусферы
(это уравнение для нижней полусферы 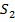 ). На
). На  внешняя нормаль составляет с осью
внешняя нормаль составляет с осью 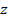 острый угол, на
острый угол, на  – тупой.
– тупой.
Поэтому

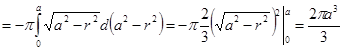 .
.
Аналогично, так как на  выполняется равенство
выполняется равенство 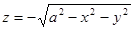 , а нормаль составляет с осью
, а нормаль составляет с осью 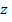 тупой угол,
тупой угол,
 .
.
Значит,
 .
.
Поэтому 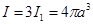 .
.
|
|
|


