 |
§5. Формула Остроградского-Гаусса
|
|
|
|
§5. Формула Остроградского-Гаусса
Теорема 5. 1. Пусть  – замкнутая кусочно-гладкая поверхность, ограничивающая тело
– замкнутая кусочно-гладкая поверхность, ограничивающая тело  в пространстве. Пусть выбрана внешняя сторона
в пространстве. Пусть выбрана внешняя сторона  . Пусть P, Q, R – функции, имеющие непрерывные производные на
. Пусть P, Q, R – функции, имеющие непрерывные производные на  . Тогда
. Тогда
 .
.
Равносильная формулировка:
 ,
,
где  − внешняя нормаль к S.
− внешняя нормаль к S.
► Предположим, что тело  ограничено сверху поверхностью
ограничено сверху поверхностью 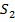 заданной уравнением
заданной уравнением  , снизу поверхностью
, снизу поверхностью  , заданной уравнением
, заданной уравнением 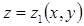 ,
,  , а сбоку – цилиндрической поверхностью
, а сбоку – цилиндрической поверхностью  .
.
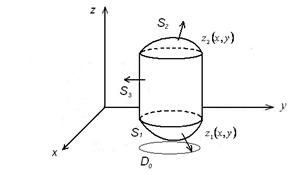
Вычислим тройной интеграл, используя теорему 2. 3:

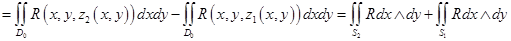 ,
,
так как на поверхности 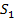 внешняя нормаль составляет с осью
внешняя нормаль составляет с осью 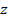 тупой угол и согласно пункту 4. 2 имеет место равенство
тупой угол и согласно пункту 4. 2 имеет место равенство
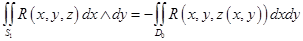 .
.
Далее, на боковой поверхности  выполнено равенство
выполнено равенство  и, следовательно,
и, следовательно,
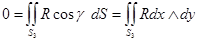 .
.
Итак, суммируя полученные интегралы, приходим к формуле
 .
.
Если поверхность  можно представить в виде объединения поверхностей
можно представить в виде объединения поверхностей  ,
,  ,
,  и цилиндрической поверхности с образующей, параллельной оси
и цилиндрической поверхности с образующей, параллельной оси 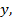 то
то

Далее, если поверхность  можно представить в виде объединения поверхностей
можно представить в виде объединения поверхностей 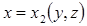 ,
, 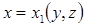 ,
,  и цилиндрической поверхности с образующей, параллельной оси
и цилиндрической поверхности с образующей, параллельной оси  то
то
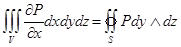 .
.
Поэтому, если поверхность S удовлетворяет условиям всех трёх случаев, то
 .
.
Теперь предположим, что тело  состоит из конечного числа тел
состоит из конечного числа тел 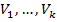 , разделённых гладкими поверхностями
, разделённых гладкими поверхностями  причём все эти тела
причём все эти тела  удовлетворяют сформулированным выше условиям. Для простоты, пусть
удовлетворяют сформулированным выше условиям. Для простоты, пусть 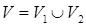 , S1 ограничивает V1, S2 ограничивает V2, S ограничивает V:
, S1 ограничивает V1, S2 ограничивает V2, S ограничивает V:
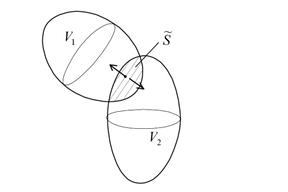
Тогда:
 .
.
Каждый из интегралов
 ,
,
преобразуем по формуле Остроградского-Гаусса:

 ,
,  ,
,
где взяты внешние стороны поверхностей 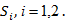
Поверхности  и
и 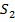 имеют общую часть
имеют общую часть 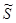 , причём их внешние нормали на поверхности
, причём их внешние нормали на поверхности 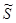 противоположны и, следовательно, интегралы по
противоположны и, следовательно, интегралы по 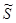 взаимно сократятся, поэтому
взаимно сократятся, поэтому
|
|
|

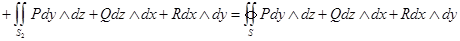 .
.
Тем самым,
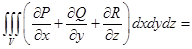
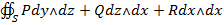
и теорема доказана. ◄
§6. Формула Стокса
Теорема 6. 1. Пусть  – гладкая ориентированная двусторонняя поверхность (т. е. выбрано направление нормали) и
– гладкая ориентированная двусторонняя поверхность (т. е. выбрано направление нормали) и  – кусочно гладкая кривая, ограничивающая
– кусочно гладкая кривая, ограничивающая  , причём мы считаем направление обхода кривой
, причём мы считаем направление обхода кривой  положительным ( см. рис). Пусть функции
положительным ( см. рис). Пусть функции  – непрерывно дифференцируемые. Тогда
– непрерывно дифференцируемые. Тогда
 .
.

Замечание 1. Равносильная формулировка теоремы:
 .
.
Замечание 2. В случае плоской кривой  , лежащей на плоскости
, лежащей на плоскости  и функций
и функций  ,
, 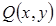 эта формула совпадает с формулой Грина.
эта формула совпадает с формулой Грина.
Замечание 3. Формулы в правой части запомнить непросто. Поэтому удобно записать подынтегральное выражение в виде определителя: 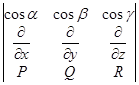 .
.
Разумеется, это не совсем обычный определитель. Ведь во второй строке его стоят операторы дифференцирования. Поэтому условимся считать, что мы понимаем под этим определителем его формальное разложение по первой строке, причём произведение, например, оператора 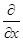 на функцию R есть
на функцию R есть 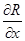 и т. п.
и т. п.
Подробнее,  =
=  -
-  +
+  =
=  -
-  -
-  + +
+ + 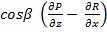 +
+ 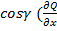 -
- 
Что совпадает с подынтегральным выражением в правой части формулы Стокса (см. замечание 1).
► Вычислим, например,  . Пусть, для простоты, поверхность S задана явным уравнением z = z(x, y), а кривая L имеет параметрические уравнения x = x(t), y=y(t), z=z(t), t
. Пусть, для простоты, поверхность S задана явным уравнением z = z(x, y), а кривая L имеет параметрические уравнения x = x(t), y=y(t), z=z(t), t  [ T0, T1], причем x = x(t), y=y(t), z=z(t) непрерывно дифференцируемые функции.
[ T0, T1], причем x = x(t), y=y(t), z=z(t) непрерывно дифференцируемые функции.
Проекция в кривой L на плоскость z=0 имеет параметрические уравнения x = x(t), y=y(t), t  [ T0, T1]. Кривая l ограничивает на плоскости OXY область D, причем изменению параметра от T0 до T1 соответствует положительное направление обхода кривой l.
[ T0, T1]. Кривая l ограничивает на плоскости OXY область D, причем изменению параметра от T0 до T1 соответствует положительное направление обхода кривой l.

Докажем, что 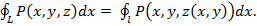
Действительно, по теореме 3ю2 имеют место равенства:

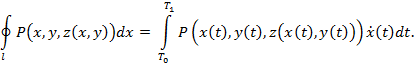
Правые части равенства совпадают, значит, равны и их левые части, что и утверждалось.
К плоской кривой 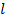 применим формулу Грина( теорема 3. 3):
применим формулу Грина( теорема 3. 3):
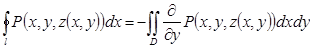 ,
,
где D – ограничиваемая кривой 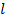 область плоскости
область плоскости 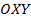 . По теореме о производной сложной функции вычислим
. По теореме о производной сложной функции вычислим
|
|
|

 .
.
Итак,  .
.

Далее,  . Докажем равенство
. Докажем равенство
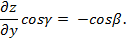
Действительно, нормаль ( 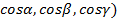 к поверхности S является нормалью к касательной плоскости к S, которая задается уравнением
к поверхности S является нормалью к касательной плоскости к S, которая задается уравнением
 =0.
=0.
Следовательно, вектор (  пропорционален вектору (
пропорционален вектору ( 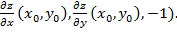
(Напомним, что вектор нормали к плоскости Ax+By+Cz+D=0 имеет координаты, пропорциональные координатам вектора (A, B, C). )
Таким образом,  =
= 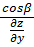 =
= 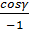 ,
,
откуда 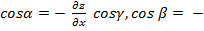
 .
.
Значит, 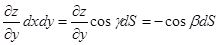 . Поэтому
. Поэтому
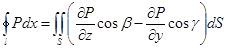 .
.
Аналогично получаем равенства
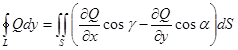 ,
, 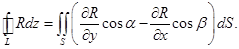
Следовательно,
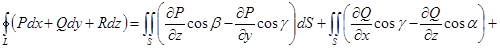
 .
.
Формула Стокса доказана. ◄
|
|
|


