 |
§4. Соленоидальное поле. §5. Циркуляция, ротор. Векторная формулировка теоремы Стокса. Приложение 1. Дифференциальные формы
|
|
|
|
§4. Соленоидальное поле
Определение. 
- соленоидальное поле, если 
.
Векторная линия обладает тем свойством, что в любой ее точке вектор касательной к линии совпадает с .
Векторная трубка – это совокупность векторных линий.
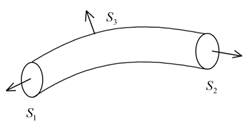
Пусть 
- сечения векторной трубки и 
- ее боковая поверхность. 
. Рассмотрим внешнюю нормаль к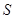 
и применим теорему Остроградского: 
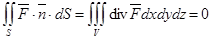, в случае соленоидального поля. Итак,
.
На , по определению векторной линии, выполняется равенство 
, поэтому 
или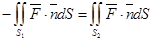 
. Изменяя направление нормали на 
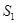на противоположное, получаем, что:
поток соленоидального поля через поперечные сечения векторных трубок постоянен.
§5. Циркуляция, ротор. Векторная формулировка теоремы Стокса
Пусть 
- контур с заданным направлением обхода, - векторное поле, 
- единичный вектор касательной к кривой. Определим циркуляцию как интеграл 
(смысл – работа силы вдоль контура ).
Введем систему координат. Пусть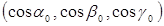 
- направляющие косинусы 
, 
- координаты .
Тогда
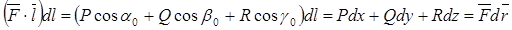
и циркуляция представляет собой интеграл 
.
Для заданного непрерывно-дифференцируемого поля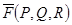 
определим ротор (или вихрь ) этого поля:
.
Легко проверить свойства ротора.
-
-
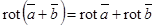
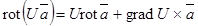, где 
обозначает векторное произведение этих векторов.
Вспомним теперь теорему Стокса:
,
где 
- непрерывно дифференцируемые функции, 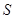- кусочно-гладкая поверхность, - ее край, причем направление обхода относительно выбранной стороны 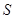является положительным.
Вспомним, что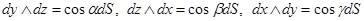 
, где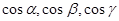 
- направляющие косинусы к выбранной стороне.
При этом правая часть формулы Стокса принимает вид
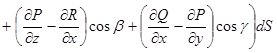или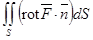 
.
Итак, в сделанных выше предположениях теорема Стокса выглядит так:
|
|
|
.
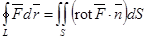Дадим определение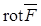 
без использования системы координат. Пусть 
- точка, 
- плоскость, в которой лежит окружность 
радиуса 
с центром в .
Тогда, по теореме о среднем, ввиду непрерывности подынтегральной функции
 .
Здесь точка  близка к  . По теореме Стокса,
 или
|
.
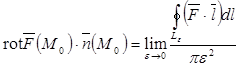Ввиду произвольности выбора плоскости, получаем проекцию 
на произвольную ось 
. Это определяет и сам вектор.
Легко вычислить, что 
.
Можно доказать и обратное. Если область односвязная и векторное поле удовлетворяет условию 
, то - потенциальное, т. е. существует функция 
такая, что 
.
Отметим, что выводы о независимости интеграла от формы пути интегрирования, сделанные для двумерного случая, полностью переносятся и на трехмерный случай. Полученное там условие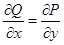 
и условие т. е. равенства 
, вполне аналогичны.
Приложение 1.
Дифференциальные формы
Составители: Макаров Ю. Н., Лужина Л, М., Чирский В. Г.
Дифференциальными формами первой, второй и третьей степени, соответственно, от переменных 
, 
, 
называются выражения:
1) 
,
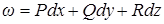2) 
,
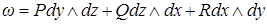3) 
,
где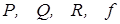 
– функции от переменных 
; 
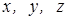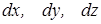– дифференциалы соответствующих переменных.
Операция внешнего произведения (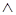 
) обладает следующими свойствами: если 
– произвольные дифференциальные формы, то:
1) 
,
2) 
,
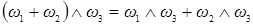3) если, кроме того, 
и 
– формы первой степени, то 
; в частности, если 
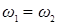, то 
.
Замена переменных в дифференциальных формах
1) Если 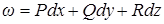и 
, 
, 
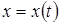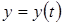- дифференцируемые функции, то
.
2) Если 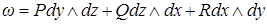и 
, 
, 
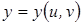- дифференцируемые функции, то
.
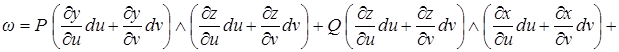
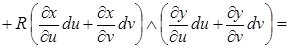
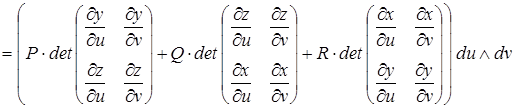3) Если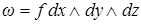 
, а 
, 
, 
– дифференцируемые функции, то
.
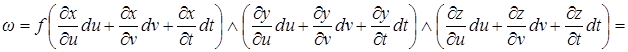
Внешние дифференциалы от формы
1) Если 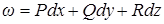, то внешним дифференциалом формы 
называют выражение:
.
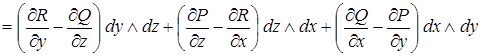В частности, если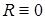 
и 
, то
.
2) Если 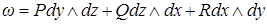, то
.
Интегралы от дифференциальных форм
1) Пусть 
– гладкая кривая в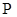 
, заданная уравнениями: , , , 
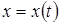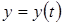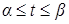. Тогда, по определению, положим:
|
|
|
.
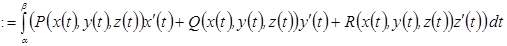Обозначим:
– векторное поле;
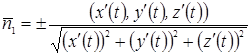– касательный вектор к . Выбор знака «+» или «–» определяет ориентацию кривой ;
– дифференциал дуги кривой ;
.
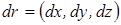Тогда мы можем кратко записать
.
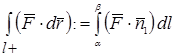Этот интеграл называют циркуляцией вектора 
по ориентированной кривой .
В частности, если 
, то
,
где 
– длина кривой .
2) Пусть 
– гладкая поверхность, задаваемая дифференцируемыми функциями 
, 
, 
, 
, где 
– некоторая ограниченная замкнутая связная область.
Тогда, по определению,
.
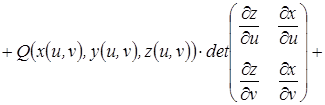
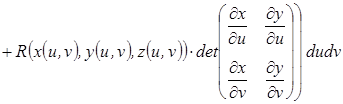Обозначим, как и выше,
;
, 
;
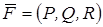– нормальный вектор поверхности (выбор знака «+» или «–» определяет ориентацию поверхности); 
– дифференциал поверхности и .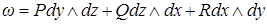
Тогда краткая запись интеграла от формы по поверхности может быть представлена в виде:
.
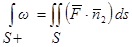Интеграл в правой части этого равенства называется потоком вектора через заданную сторону поверхности .
В частности, если 
, то
,
где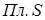 
– площадь поверхности .
Замечание. Выбор вектора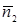 
или 
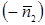определяет ориентацию поверхности (или кривой 
). При изменении ориентации поверхности (или кривой) знак интеграла меняется на противоположный.
|
|
|
