 |
Математическая модель задачи о назначениях
|
|
|
|
 ; ;
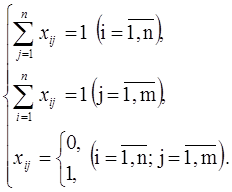
|
При решении задачи о назначениях количество работников должно равняться количеству выполняемых работ: m=n. Это условие сбалансированности задачи. Если это условие не выполняется, то имеем несбалансированную задачу, и тогда или некоторые работники останутся без работы, или некоторые работы не будут выполнены. Как и в случае транспортной задачи, несбалансированная задача о назначениях приводится к сбалансированному случаю введением фиктивных работ или фиктивных работников.
Задача о назначениях может решаться методами, аналогичными методам решения транспортной задачи. Для этой задачи также разработан алгоритм, носящий название " Венгерского метода". Суть метода состоит в выполнении следующих этапов.
1 этап:
1. Представить условия в виде транспортной таблицы.
2. В каждой строке таблицы требуется: найти наименьший элемент, затем вычесть его значение из каждого элемента данной строки.
3. В каждом столбце также найти наименьший элемент и вычесть его значение из всех элементов данного столбца. Целью задачи является распределение всех подлежащих назначению единиц в ячейки с нулевой стоимостью. Оптимальное значение целевой функции в этом случае равно нулю.
2 этап:
1. Найти строку, содержащую только одно нулевое значение, в его клетку помещается один элемент (0 обводится квадратиком). Если такие строки отсутствуют, можно начать с любой строки.
2. Зачеркнуть оставшиеся нулевые элементы данного столбца.
3. Повторять эти процедуры, пока продолжение окажется невозможным.
Если окажется, что имеется несколько нулей, которым не соответствуют назначения, и которые остались не зачеркнутыми, необходимо:
|
|
|
4. Найти столбец, содержащий только одно нулевое значение, в его клетку помещается один элемент.
5. Зачеркнуть оставшиеся нули в данной строке
6. Повторять пп. 4-5, пока продолжение указанной процедуры окажется невозможным
Если выяснится, что таблица содержит неучтенные нули - повторить пп. 1-6
Если решение является допустимым, оно оптимально. Если нет - перейти к этапу 3.
3 этап: (Если решение является недопустимым)
1. Провести минимальное количество прямых линий через столбцы и строки матрицы таким образом, чтобы они проходили через все нули, содержащиеся в таблице.
2. Найти наименьший из элементов, через которые не проходит ни одна прямая.
3. Вычесть его из всех элементов, через которые не проходят прямые.
4. Прибавить его ко всем элементам, лежащим на пересечении прямых.
5. Элементы, через которые проходит только одна прямая, оставить неизменными.
В результате в таблице появится как минимум одно новое нулевое значение. Вернуться к этапу 2 и повторить решение заново.
Пример решения задачи
Компания имеет 4 базы сбыта и 4 заказа, которые необходимо доставить потребителям. Складские помещения каждой из баз достаточны для размещения любого из этих заказов.
Составим транспортную таблицу.
| База | Потребитель | Потребитель | Потребитель | Потребитель |
| 1 | 2 | 3 | 4 | |
| A | ||||
| B | ||||
| C | ||||
| D |
В соответствии с алгоритмом решения задачи вычитаем минимальные элементы по строкам (выделены полужирным), получим новую таблицу:
| База | Потребитель | Потребитель | Потребитель | Потребитель |
| 1 | 2 | 3 | 4 | |
| A | ||||
| B | ||||
| C | ||||
| D |
Проведем ту же процедуру для столбцов:
| База | Потребитель | Потребитель | Потребитель | Потребитель |
| 1 | 2 | 3 | 4 | |
| A | ||||
| B | ||||
| C | ||||
| D |
Проводим второй этап.
|
|
|
| База | Потребитель | Потребитель | Потребитель | Потребитель |
| 1 | 2 | 3 | 4 | |
| A | ||||
| B | | |||
| C | ||||
| D | | |
Проводим прямые через 1 и 3 столбцы и через последнюю (нижнюю) строчку. Минимальный элемент, через который не проходит ни одна прямая, равен 2. Вычитаем его из всех элементов, через которые не проходят прямые, прибавляем его ко всем элементам, лежащим на пересечении прямых. Элементы, через которые проходит только одна прямая, остаются неизменными. Получаем следующий результат:
| База | Потребитель | Потребитель | Потребитель | Потребитель |
| 1 | 2 | 3 | 4 | |
| A | | |||
| B | | | ||
| C | ||||
| D | |
В начальной таблице суммируем значения в ячейках, соответствующих выбранным элементам итоговой таблицы (по диагонали - 68+60+35+45=208), это и будет минимальное решение данной задачи. Для решения такой же задачи на максимум необходимо первоначальные значения умножить на (-1), после чего производить решение по приведенному выше алгоритму.
|
|
|


