 |
Рассмотрим пример решения задачи о назначениях в Excel.
|
|
|
|
Рассмотрим пример решения задачи о назначениях в Excel.
Допустим, необходимо распределить четырех сотрудников на выполнение пяти видов занятий. Оплата за выполнение каждого вида занятий разными сотрудниками различна и приведена в следующей таблице:
|
|
Стоимость выполнения | ||||
|
Сотрудники |
Виды занятий | ||||
|
| |||||
Требуется так распределить сотрудников по занятиям, чтобы минимизировать суммарные расходы на оплату за выполнение работ. Заметим, что данная модель не сбалансирована, поскольку сотрудников меньше, чем видов занятий. Следовательно, для выполнения какого-то вида работ будет необходимо принять на работу еще одного сотрудника. Для решения этой задачи, в модели надо ввести фиктивного сотрудника.
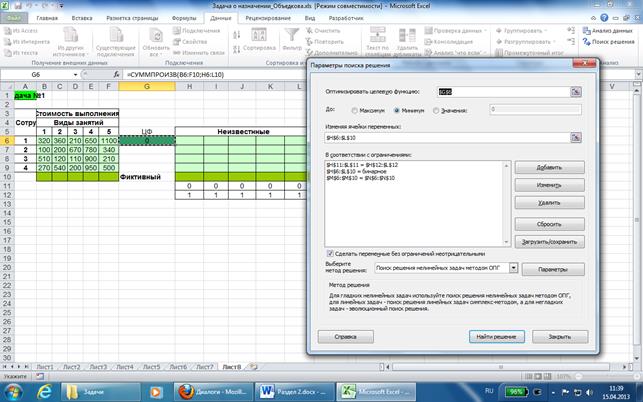
Подготовим данные на листе Excel, как показано на рисунке.
В ячейках H6: L10 расположим неизвестные.
В ячейку G6 запишем целевую функцию
=СУММПРОИЗВ(B6: F10; H6: L10) – стоимость выполнения всех работ.

В ячейках M6: M10 запишем левые части ограничений, выражающих количество выполнения работ на одного сотрудника
=СУММ(H6: L6)
=СУММ(H7: L7)
=СУММ(H8: L8)
=СУММ(H9: L9)
=СУММ(H10: L10)
В ячейках N6: N10 запишем правые части ограничений, указывающие на то, что каждый сотрудник выполняет одну работу.
В ячейках H11: L11 запишем левые части ограничений, выражающих количество сотрудников, выполняющих одну работу.
=СУММ(H6: H10)
=СУММ(I6: I10)
=СУММ(J6: J10)
=СУММ(K6: K10)
=СУММ(L6: L10)
В ячейках H12: L12 запишем правые части ограничений, выражающих тот факт, что каждую работу выполняет один сотрудник.
Вызовем «Поиск решения» и заполним окно следующим образом:
|
|
|
После выполнения получим решение:
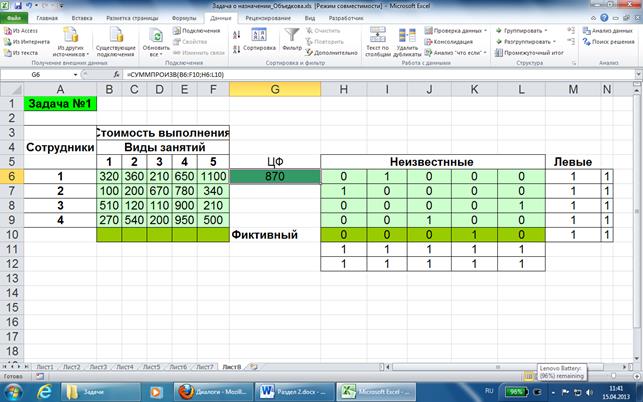
Решение задачи показывает, что для выполнения всех видов работ потребуется 870 денежных единиц. Кроме того, выполнение четвертого вида занятий возложено на фиктивного сотрудника. Это означает, что для выполнения этого вида работ требуется нанять на работу еще одного сотрудника.
2. 3 Принятие решений при многих критериях
В оптимизационных задачах, рассмотренных раньше, речь шла о единственном критерии в каждой из задач. В реальности однокритериальные задачи встречаются достаточно редко, на практике при решении задач присутствует одновременно нескольких критериев. Тогда возникает задача принятия решений с векторным критерием, или задача многокритериальной оптимизации.
Задачей многокритериальной оптимизации называется задача с несколькими критериями, которые характеризуют решения с разных сторон. Чаще всего заранее выделено направление улучшения каждого критерия, например его увеличение. Вместе с тем, одновременное увеличение сразу всех критериев является невозможным. Скажем, имея некоторую ограниченную сумму денег, нельзя купить больше и сахара, и муки. Более конкретно можно сказать так:
Имея в наличии деньги в количестве S при ценах на сахар pc и на муку рM, можно купить такое количество сахара XC и такое количество муки XM, что
pcXC + рM XM £ S,
XC ³: 0, XM ³ 0.
На рисунке показана область АВО, любая точка которой удовлетворяет этому нестрогому неравенству. Все границы включены в область допустимых значений. Нам хотелось иметь одновременно max XC и max XM, но это невозможно.
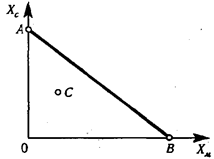
Рисунок. Соотношение между объемами покупок.
Поэтому в этой задаче, как и в других многокритериальных задачах, речь идет не об оптимальных решениях, а об эффективных.
Вектор значений показателей X* (X = (XC, XM) в нашем примере) называют эффективным (или оптимальным по Парето ), если во множестве имеющихся показателей нет другого такого, который был бы не хуже X* по всем компонентам и превосходил X* хотя бы по одной компоненте.
|
|
|
Эффективные решения – это такие решения, которые не могут быть улучшены сразу по всем критериям.
В нашем примере все точки на АВ – множество эффективных точек, а точка С – неэффективная.
Если же на объемы закупок XM, XC наложить такие ограничения:
XM ³ А, XC ³ В. Тогда ситуацию можно выразить с помощью приведенных ниже рисунков:
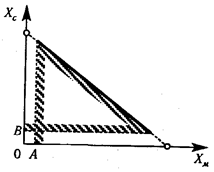
Рисунок. Есть эффективные решения при дополнительных ограничениях

Рисунок. Нет эффективных решений при дополнительных ограничениях
Выделение эффективного множества решений
Опишем один из способов выделения паретовского множества вариантов при решении многокритериальных задач, который успешно применялся, в частности, при разработке технических систем и конструкций.
Пусть проектируемая система зависит от r варьируемых параметров a1, ..., a2, для каждого из которых есть определенная область допустимых значений. Кроме этих ограничений, обычно есть еще ограничения, возникающие из-за связей параметров между собой. В целом, есть некоторая область, в которой только и могут находиться допустимые значения параметров. В этой области выбирают N штук пробных точек:

Пробные точки в области допустимых значений целесообразно располагать равномерно. Оценивание каждого варианта производится по критериям Ф1, ..., Фk, которые к примеру, все надо минимизировать. Результаты оценивают по каждому критерию и упорядочивают по возрастанию:

где i1, i2, …, iN – последовательность номеров точек (своя для каждого критерия),
j = 1, ..., k.
Пусть, например, есть два критерия Ф1, Ф2 и четыре точки a1, ..., a4 (каждая точка имеет r компонентов). Пусть оказалось, что:
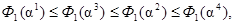
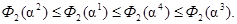
Тогда результаты испытаний и упорядочивания можно представить следующим образом:
| точки | КРИТЕРИИ | |||
| ЗНАЧЕНИЯ Ф | УПОРЯДОЧЕНИЕ ТОЧЕК | |||
| Ф1 | Ф2 | Ф1 | Ф2 | |
| Ф11 | Ф21 | |||
| Ф12 | Ф22 | |||
| Ф13 | Ф23 | |||
| Ф14 | Ф24 | |||
Затем, например, проектировщик или заказчик формулирует критериальные ограничения Ф1, ..., Ф*K, то есть, указывает худшие значения по каждому из критериев, на которые еще можно согласиться: Ф1 < Ф*K. Критериальные ограничения не являются абсолютными, они зависят от физического или экономического смысла критериев, конъюнктурных соображений и т. д. Если эти ограничения сформулированы слишком жестко, может оказаться, что вообще нет ни одного приемлемого варианта. В таком случае, придется идти на какие-то уступки, компромиссы, выбрать менее обременительные критериальные ограничения.
|
|
|
Пусть в приведенном примере Ф*1 и Ф*2 таковы, что в выбранные ограничения укладываются: по первому критерию точки 1, 2, 3, по второму – 1, 2. Тогда паретовское множество вариантов состоит из точек 1 и 2. Аналогично поступают и в общем случае, когда размерность задачи больше, чем в рассмотренном примере.
Анализ результатов, оценивание вариантов в пробных точках позволяют, в частности:
• обнаружить критерии, значения которых мало меняются;
• выявить зависимые или противоречивые критерии;
• определить взаимосвязь критериев друг с другом;
• установить влияние параметров на критерии и в ряде случаев попытаться улучшить значения тех или иных критериев за счет корректировки ограничений на параметры.
Некоторые формальные способы решения многокритериальных задач
Как же искать решение, формализовать задачу, как согласовать противоречивые стремления? Рассмотрим некоторые возможные способы действий.
Можно взять сумму критериев, в которую каждый критерий войдет с каким-то сомножителем, который можно назвать весом критерия. Либо можно каким-либо другим образом объединить (есть такой термин «свернуть») исходные критерии в один. Можно критерии предварительно упорядочивать по важности, а затем последовательно решать несколько оптимизационных задач, при этом число задач будет равно числу критериев, в порядке убывания важности этих критериев.
Если после упорядочивания критериев по важности оказывается, что первый критерий К1 существенно важнее всех остальных, критерий К2 намного важнее всех критериев, кроме К1, критерий К3 существенно важнее всех, кроме К1 и К2, и т. д., то естественно считать, что i-ое решение (альтернативу) лучше j-го решения (j-ой альтернативы), когда это i-ое решение лучше j-го по критерию К1. Если i-ое и j-ое решения эквивалентны по К1, то предпочтение отдается лучшему по критерию К2, и т. д. Такое упорядочение называется лексикографическим, оно возможно лишь при значительной неравноценности критериев. В приводимой таблице дается пример такого упорядочивания пяти альтернатив А1, .... A5 по четырем критериям К1, .... К4. В клетках – значения аij для i-ой альтернативы по j-му критерию.
|
|
|
Результаты многокритериального оценивания
| A | К | ||||
| К1 | К2 | К3 | К4 | место | |
| А1 | II | ||||
| А2 | III | ||||
| А3 | I | ||||
| А4 | IV | ||||
| А5 | V | ||||
По каждому критерию хотим иметь максимум, К1 – самый важный, К4 – самый неважный.
Можно для каждого критерия сразу задать границу, за которую не должны выходить значения критерия, и искать оптимальное решение поочередно по каждому критерию. При этом считаем, что остальные укладываются в заданные границы, то есть практически сразу вводим дополнительные ограничения, которые могут появляться из каких-то соображений или решения оптимизационных задач, внешних по отношению к данной задаче. Иногда используют парные сравнения значений критериев.
Для примера с мукой и сахаром можно было бы искать решение, задавшись дополнительным ограничением снизу на объем закупки, например, сахара: xc < x0c.
Тогда получилась бы просто однокритериальная задача:
xM® max;
Рмхм + рсхс £ S;
xC ³ x0c;
xM ³ 0
В данной простой ситуации решение находится сразу из финансового ограничения или из графика. В более сложном случае, когда имеем большое количество переменных, критериев и ограничений, задача становится намного сложнее.
Следующий способ решения многокритериальных задач является достаточно распространенным. Решают оптимизационную задачу с одним первым критерием, считая, что других критериев нет. Потом решают задачу с одним вторым критерием. И так далее. Сначала выявляются те экстремальные уровни, которые в принципе достижимы по каждому критерию в отдельности. Для каждого критерия, начиная с наиболее важного, задается пороговое значение, которое не должно нарушаться. Затем условие нерушимости порога по первому критерию считается ограничением, решается задача оптимизации для второго критерия, далее добавляются ограничения по порогу второго критерия, решается задачу для третьего критерия и т. д. Поясним сказанное примером.
Предприимчивая тетя покупает в одном месте мужские свитера (в количестве не более 60 штук), в другом – женские (не более 40 штук). С помощью мягкой щетки она делает начес и продает по 2 условные единицы за мужские и по 4 единицы за женские. За некоторый единичный интервал времени она может начесать не более 80 свитеров. Поскольку тетя хочет удержаться и на рынке мужских свитеров (пусть их индекс М), и на рынке женских свитеров (пусть их индекс Ж), постольку она интересуется не максимумом дохода или прибыли, а оценками сразу по нескольким критериям. Пусть закупочные цены в условных единицах таковы: мужские свитера по 1 ед/шт., женские по 2 ед/шт. Оптимизационная задача тети выглядит так (xM, xЖ – объемы закупок):
|
|
|

Рисунок. Иллюстрация к примеру задачи с тремя критериями
К1 = 2хм ® max;
К2 = 4xж ®mах;
К3 = хм + 2xж ® min;
0 £ хм £. 60;
0 £ xж £ 40;
хм + xж £ 80.
На рисунке показана допустимая область OABCD, направления благоприятных изменений критериев К1, К2, К3. Отдельно по каждому из критериев решения находятся сразу (по К1: хм = 60 К1 = 120; по К2: xж = 40, К2 = 160; по К3: хм = xж = 0, К3 - 0);
Зная значения критериев для однокритериальных задач, ситуацию на рынках и свои финансовые возможности, эта тетя выбирает такие пороги: П1 = 100 (то есть она хочет иметь К1³ . П1 = 100), П2 = 112 (хочет иметь К2 ³ П2 = 112) и П3 = 120 (К3£ П3 = 120).
Сначала она решает такую задачу:
хм £. 60;
xж £ 40;
хм + xж £ 80.
2хм ³ 100
(что дает хм ³ 50, xж £ 30) с целевой функцией 4xж ® max. Решением будет xж = 30, К2 = 120 ³ 112. Затем решается задача:
хм £. 60;
xж £ 40;
хм + xж £ 80;
2хм ³ 100;
4xж ³ 112
(что дает хм ³ 50, xж ³ 28) с целевой функцией хм + 2xж ® min. Ясно, что решением будет хм = 50, xж = 28 с К3 = 106 £ 120 = П3. чем и завершится данная задача. Если бы было П3 = 95, то решения в данной задаче не существовало.
Важно, что каждый из способов работы со многими критериями возможен только при определенных условиях, в каких-то рамках. При решении многокритериальных задач появляются специфические проблемы, которых нет в однокритериальных задачах, и эти проблемы зачастую не удается до конца разрешить. Поэтому работа с многокритериальными задачами всегда трудна и требует высокой квалификации исследователя.
|
|
|


