3. Принятие решений в условиях неопределенности и риска

Вопросы к разделу.

1. В чем состоит особенность задачи принятия оптимальных решений?

2. Какие основные проблемы вызывают задачу принятия решений?

3. В каких случаях возникают ограничения при привлечении экспертов к принятию оптимальных решений?

4. В чем преимущество использования компьютерных систем?

5. Какие системы и прикладные программы используют при принятии решений?

6. Для чего применяются системы поддержки принятия решений?

7. Каковы основные этапы построения математической модели задачи принятия решений?

8. Какие основные типы задач принятия решений в зависимости от вида информации в подсистеме о состоянии среды Вы знаете?

9. Какие Вы знаете типы задач принятия решений в зависимости от мощности множества критериев?

10. Какие существуют отношения между оптимальной альтернативой и критерием целевой функции?

11. Для каких задач требуется использование методов исследования функции на экстремум?

12. В чем состоит метод множителей Лагранжа?

13. Какие задачи решаются методом линейного программирования?

14. Какие системы Microsoft Office применимы для решения оптимизационных задач?

15. В чем заключается венгерский метод решения задачи назначений?

16. В чем состоит задача многокритериальной оптимизации?

17. Как формулируется оптимальность по Парето?

18. Какие Вы знаете способы выделения эффективного множества решений?

3. Принятие решений в условиях неопределенности и риска

3. 1 Принятие решений в условиях неопределенности.

В разделе 2 рассмотрен процесс построения математической модели задачи принятия решения (ЗПР), который состоит в задании трех множеств: X – множества допустимых альтернатив; Y – множества возможных состояний среды; A – множества возможных исходов. Каждой паре (х, у), определяющей состояние управляемой подсистемы, и состоянию среды соответствует определенный исход из множества A - определена функция реализации F. Функция реализации каждой паре (альтернатива, состояние среды) ставит в соответствие определяемый этой функцией исход.

Набор объектов < X, Y, F, A> представляет реализационную структуру принятия решения. Эта структура выражает связь между выбранной альтернативой и исходом, которая в общем случае не является однозначной, или детерминированной. Каждый конкретный исход зависит не только от выбранной альтернативы, но и от состояния среды.

Принятие решений в условиях неопределенности соответствует такому случаю, когда лицу, принимающему решение, при выборе альтернативы неизвестна существующая в настоящий момент реализация состояния среды, и нет информации о вероятностях их появления. Тем не менее, эта неопределенность не является абсолютной, поскольку известны множество возможных состояний среды ( Y – множества) и функция реализации F.

Оценочная структура задается способом, аналогичным тому, который применяется при принятии решений в условиях определенности, с точки зрения эффективности выбранного решения. Целевая функция также будет являться функцией полезности либо функцией потерь в зависимости от условий задачи.

Следовательно, математическая модель задачи в условиях неопределенности задается в виде тройки объектов:

< X, Y, f>.

Где X – множества допустимых альтернатив; Y – множества возможных состояний среды; f – целевая функция, являющаяся композицией функции реализации F и оценочной функции 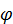, то есть .

Рассмотрим пример построения математической модели в условиях неопределенности из книги В. В. Розена «Математические методы принятия решений в экономике».

Задача «Аренда отеля».

Предприниматель собирается взять в аренду отель сроком на 1 год. Имеются отели четырех типов с количеством комнат: 20, 30, 40, 50. Все расходы, связанные с содержанием отеля, должен оплачивать арендатор. Расходы в некоторых денежных единицах состоят из трех частей:

1) Расходы, не зависящие от числа комнат отеля:

a) Благоустройство территории – 10000 денежных единиц;

b) Затраты на текущий ремонт и содержание – 1500 ден. ед.;

c) Ночное дежурство – один дежурный 6000 ден. ед.;

d) Уборка территории – один служащий 8000 ден. ед.

2) Расходы, зависящие от числа комнат отеля:

a) меблировка одной комнаты – 2000 ден. ед.;

b) 1 горничная на 10 комнат – 6000 ден. ед.;

c) содержание одной комнаты 150 ден. ед.;

d) страхование на случай пожара для одной комнаты – 25 ден. ед.

3) Расходы, зависящие от числа занятых комнат отеля:

a) стирка, уборка – 25 ден. ед. на комнату;

b) электричество, вода, газ – 25 ден. ед. на комнату.

Доход предпринимателя составляет 200 ден. ед. в день с каждой занятой комнаты. Какое решение должен выбрать предприниматель – какой отель взять в аренду?

Начнем с построения математической модели задачи.

В качестве множества альтернатив представлены типы отелей, поэтому Х={20, 30, 40, 50}. Среда в данной задаче – то, что определяет при каждой выбранной альтернативе появление конкретного исхода, результата. Здесь в качестве исхода выступает прибыль, которую предприниматель получит за год аренды отеля. При фиксированной альтернативе  прибыль полностью определяется средним числом занятых комнат у. То есть, в качестве единственного параметра, характеризующего состояние среды, здесь выступает среднегодовой спрос. Следовательно, в качестве множества состояний среды в данной задаче можно взять Y={1, 2, …, 50}

Целевая функция f(x, y) выражает прибыль, которую получит предприниматель за год в ситуации, когда он арендует отель из х комнат, а среднегодовой спрос равен у. Выразим целевую функцию в явном виде.

1) Расходы, не зависящие от числа комнат отеля составляют

10000 + 1500 + 6000 + 8000 = 25500 (денежных единиц).

2) Расходы, зависящие от числа комнат отеля х, составляют:

2000 x + 600 x + 150 x + 25 x = 2775 x (денежных единиц).

3) Расходы, зависящие от числа у занятых комнат, равны:

365·(25 у + 25 у) = 18250 у (денежных единиц).

4) Доход предпринимателя определяется числом занятых комнат и составляет в год

365·200 y = 73000 y (денежных единиц).

Тогда прибыль предпринимателя за год в рассмотренной ситуации равна

73000 y – (2775 x + 18250 y + 25500) = 54750 y – 2775 x – 25500 (денежных единиц).

Целевая функция данной задачи такова:

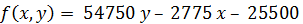
Таким образом, целевая функция f(x, y) является функцией двух аргументов. Главная сложность при принятии решения в условиях неопределенности состоит в том, что выбирая значение альтернативы – аргумента х из множества X ( ), лицо, принимающее решение, не знает значения аргумента

Рассмотрим случай, когда множества X и Y являются конечными, и целевая функция может быть задана в виде таблицы. Пусть элементы множества Х различаются по номерам i от 1 до m, элементы множества Y по номерам j от 1 до n: X={1, 2, …, i, …, m }, Y={1, 2, …, j, …, n }. Обозначим значение целевой функции  и будем интерпретировать числа 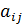 как выигрыши принимающего решение в ситуации (i, j).

Тогда целевая функция задается в виде таблицы, в которой на пересечении i –ой строки и j –го столбца находится  - выигрыш принимающего решение, когда он выбирает альтернативу i, в то время как среда принимает состояние j. Такая таблица называется таблицей выигрышей или платежной матрицей.

Выбор альтернативы в таком случае осуществляется с помощью применения методов теории игр.

Одним из принципов, по которым можно сравнить две существующие альтернативы, является принцип доминирования. На принципе доминирования и дублирования альтернатив основан метод упрощения платежной матрицы.

Введем следующие определения принципов, применяемых для упрощения платежной матрицы.

Определение. Дублирующими называются альтернативы, у ко­торых соответствующие элементы платежной матрицы одинаковы.

Определение. Если все элементы i-ой строки платежной матрицы больше соответствующих элементов k-ой строки, то i-ая альтернатива А называется доминирующей над k-ой альтернативой. Каким бы ни было состояние среды, доминирующая альтернатива является не менее предпочтительной для принятия решения, чем доминируемая альтернатива. Следовательно, доминируемую альтернативу можно отбросить. Принцип доминирования состоит в исключении доминируемых альтернатив, вследствие чего уменьшается размер платежной матрицы, и процесс принятия решения упрощается.

Пример. Рассмотрим некоторую абстрактную задачу принятия решения в условиях неопределенности, целевая функция которой представлена платежной мат­рицей:

Альтернативы	Состояние среды
	I	II	III	IV	V	VI

 

Необходимо выбрать оптимальную альтернативу в заданных условиях.

    Упростим платежную матрицу, используя принцип доминирования альтернатив.

Альтернатива 4 доминирует альтернативу 5, поскольку все элементы строки альтернативы 4 не меньше элементов строки альтернативы 5, также альтернатива 3 доминирует альтернативу 1. Тогда альтернативы 5 и 1 можно исключить из рассмотрения, а оставшиеся альтернативы являются несравнимыми с точки зрения доминирования. Получаем упрощенную платежную матрицу:

Альтернативы	Состояние среды
	I	II	III	IV	V	VI

 

Отметим, что сравнение альтернатив по отношению доминирования аналогично сравнению исходов многокритериальной задачи принятия решений по Парето-доминированию, которое рассматривалось в разделе 2. В задаче принятия решений в условиях неопределенности столбцам соответствуют разные состояния среды, а в многокритериальной задаче разным столбцам соответствуют различные критерии.

После упрощения платежной матрицы необходимо из оставшихся альтернатив выбрать оптимальную. Рассмотрим метод выбора оптимальной альтернативы в условиях неопределенности.

Выдвигается некоторая гипотеза о состоянии среды, которая позволяет присвоить каждой альтернативе единую числовую оценку. Числовая оценка дает критерий сравнения альтернатив по предпочтению, который заключается в том, что из двух альтернатив лучшей считается та, которая имеет большую числовую оценку. Если альтернативы имеют одинаковые оценки, они считаются эквивалентными. Оптимальной альтернативой будет являться та альтернатива, которая окажется наиболее предпочтительной, а именно, имеет наибольшую числовую оценку в случае функции полезности и наименьшую в случае функции потерь.

Разработан целый ряд критериев для сравнения альтернатив. Наиболее применимыми являются следующие.

Критерий Лапласа.

Критерий Лапласа применим в ситуации, когда информация о состояниях среды ничтожно мала. Он основан на принципе недостаточного основания Лапласа, согласно которому можно считать, что все состояния среды равновероятностны. Оценка i-ой альтернативы производится по формуле:

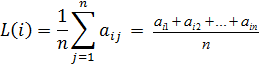
Лучшей альтернативой будет считаться та, которая имеет более высокую оценку по критерию Лапласа. Тогда оптимальной альтернативой будет максимальная из рассматриваемых:

Согласно критерию Лапласа, выбирается альтернатива, для которой среднее арифметическое элементов со­ответствующей строки максимальное.

Недостатком критерия Лапласа является то, что при нахождении среднего выигрыша может произойти «эффект компенсации» маленьких выигрышей большими, а полученное среднее арифметическое выигрыша окажется слабой характеристикой допустимых альтернатив. Например, применим критерий Лапласа для сравнения альтернатив следующего примера:

Альтернативы	Состояние среды
	I	II	III	IV	V	VI	VII	VIII	IX	X
	9, 9									10, 1

 

 Получим, что альтернатива 1 более предпочтительна, чем альтернатива 2, поскольку среднее арифметическое выигрыша 1 альтернативы 101/10=10, 1, а второй альтернативы 100/10=10. То есть, получили, что средний выигрыш альтернативы 1 больше выигрыша альтернативы 2.

Заметим, тем не менее, что выигрыши альтернативы 1 распределены очень неравномерно, поэтому в случае выбора альтернативы 1 можно получить нулевой выигрыш, а при выборе альтернативы 2 в наихудшем варианте имеется гарантированный выигрыш 9, 9

Критерий Вальда.

Критериq Вальда основан на гипотезе антагонизма, которая означает, что при выборе надо рассчитывать на самый худший вариант, то есть это соответствует максиминной стратегии теории игр. Оценка i-ой альтернативы производится по формуле:

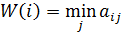
В этом случае оптимальная альтернатива выбирается из условия максимизации оценки W(i):

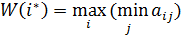
Число  называется максимином. Принцип оптимальности, которому соответствует выбор максиминной альтернативы, называется принципом максимина.

Оценка W(i) показывает гарантированный уровень выигрыша при выборе i-ой альтернативы, поскольку при выборе этой альтернативы выигрыш независимо от состояния среды будет не меньшим, чем W(i). Принцип максимина, таким образом, основан на максимизации гарантированного минимального выигрыша, иногда этот принцип называют принципом максимального гарантированного результата. Этот критерий является пессимисти­ческим, поскольку считается, что среда будет действовать наихудшим для человека способом.

Ориентация на наихудший вариант является главным недостатком принципа максимина. Рассмотрим пример.

 

Применим критерий Вальда при выборе альтернатив, заданных следующей платежной матрицей:

Альтернативы	Состояние среды
	I	II	III	IV	V	W(i)

 

В этом случае альтернатива 1 будет предпочтительней альтернативы 2, несмотря на то, что за исключением состояния среды II, во всех остальных случаях альтернатива 2 доминирует альтернативу 1.

В случае, когда целевая функция является функцией потерь, Оценка i-ой альтернативы производится по формуле:

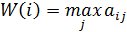
В этом случае оптимальная альтернатива выбирается из условия минимизации оценки W(i):

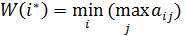
Число  называется минимаксом. Принцип оптимальности, которому соответствует выбор минимаксной альтернативы, называется принципом минимакса. Принцип минимакса является принципом минимизации максимальных потерь.

Критерий максимума.

Критерий максимума выбирается из условия

.

Критерий максимума является критерием крайнего оптимизма, поскольку принимается, что среда будет наиболее благоприятна для человека.

Критерий Гурвица.

В этом случае для оценки поведения среды вводится показатель пессимизма α, который изменяется в пределах от 0 до 1. В соответствии с критерием Гурвица рекомендуется выбрать альтернативу, опре­деляемую по формуле

Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения среды. При α = 1 критерий превращается в критерий крайнего пессимизма Вальда, при α = 0 - в критерий крайнего оптимизма, критерий максимума. При выборе значения α главную роль играет степень ответственности лица, принимающего решение по вы­бору альтернативы. Чем больше последствия ошибочных решений, тем больше желания застраховаться, и значение α выбирается ближе к единице.

Сложность использования критерия Гурвица проявляется при нахождении показатель пессимизма. Кроме того, к недостаткам этого метода можно отнести тот факт, что при принятии решения учитываются только две альтернативы – наилучшая и наихудшая

Критерий Сэвиджа.

Суть критерия Сэвиджа состоит в таком выборе альтернативы, которая не допустит чрезмерно высоких потерь в случае ее выбора. Для этого определяется матрица рисков, другими словами, матрица сожалений, элементы ко­торой показывают, какой убыток понесет принимающий решение, если для каждого состояния среды он не выберет наилучшей альтернативы. Риском r_ij при выборе альтернативы i в состоянии среды j называется число, определяемое по формуле . Риск имеет смысл меры сожаления лица, принимающего решение, от незнания состояния среды, проявляющееся в том, что если бы он знал состояние среды, он выбрал бы  вместо a_ij.

Вводится матрица рисков следующего вида:

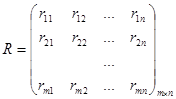
Оптимальная альтернатива определяется выражением, минимизирующим максимальный риск:  Здесь, таким образом, используется минимаксный критерий для матрицы сожалений

При принятии решений в условиях неопределенности оптимальные решения при использовании различных критериев в общем случае будут разные, поэтому следует оценивать различные варианты с точки зрения нескольких крите­риев. Если рекомендации совпадают, можно с большей уверенно­стью выбрать наилучшее решение; если рекомендации противоре­чат друг другу, окончательное решение надо принимать с учетом его сильных и слабых сторон.

Рассмотрим пример из книги В. В. Розена «Математические методы принятия решений в экономике».

Пример. Выбор электростанции для строительства.

Необходимо выбрать проект электростанции.

Возможно строительство электро­станций по четырем типам проектов: А1 -тепловые, А2 - приплотинные, А3 - бесшлюзовые, А4 - шлюзовые. Последствия строительства и эксплуатации электростанции каждого типа зависят от ряда неопределенных факторов, которые можно представить в виде различных состояний среды. Допустим, можно выделить четыре сочетания различных факторов, определяющих четыре состояния среды В1, В2, В3, В4. Экономическая эффективность электростанции, выраженная как процент прироста доходов в течение одного года эксплуатации электростанции, зависит как от типа электростанции, так и от состояния среды и задана матрицей

Типы электростанций	Состояние среды
	В1	В2	В3	В4
А1
А2
А3
А4

 

1). Определим альтернативу по критерию Вальда

следует строить бесшлюзовую электростанцию.

2). Теперь сделаем выбор по критерию Сэвиджа. Построим матрицу рисков:

В соответствии с критерием минимизации максимальных рисков Сэвиджа, получим

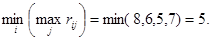
Тогда при использовании критерия Сэвиджа, оптимальным является строить бесшлюзовую электростанцию.

3). Сделаем оценку по критерию Гурвица. Предположим,  

Откуда следует, что надо принять решение о строительстве приплотинной элек­тростанции.

4). Если принять известным распределение вероятностей для различных состояний природы, например, считать эти состояния равновероятностными

 то для принятия ре­шения следует найти математические ожидания выигрыша:

Так как максимальное значение имеет М₃, то следует строить бесшлюзовую электростанцию.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: