 |
3.2 Принятие решений в условиях риска.
|
|
|
|
3. 2 Принятие решений в условиях риска.
При рассмотрении ситуации принятия решений в условиях определенности и неопределенности было введено понятие реализационной структуры в виде набора объектов < X, Y, F, A> . Эта структура выражает связь между выбранной альтернативой и исходом. Каждый конкретный исход зависит не только от выбранной альтернативы, но и от состояния среды.
Построение реализационной структуры предполагает задание функции реализации F(x, y). Трудность состоит в том, что переменные x, y в этой функции неравноправны: поведение управляющей системы имеет целенаправленный характер, в то время как поведение среды может иметь как целенаправленный, так и случайный, стохастический характер. Если поведение среды обусловлено стохастическими процессами, то принятие решений в этом случае осуществляется в условиях риска. Это состояние можно описать в виде существования некоторой вероятностной меры, соответствующей тому или иному состоянию среды. При этом лицо, принимающее решение, имеет определенную информацию о вероятностях этих состояний среды. Такого рода информация может быть разного характера. Например, может быть известно, что одно состояние более вероятно, чем другое, но могут быть и более определенные признаки сравнения вероятностей состояний, например, что вероятность состояния А1 вдвое выше вероятности состояния А2.
Некоторые необходимые сведения из теории вероятностей.
Под случайной величиной понимают величину, которая в результате опыта со случайным подходом принимает то или иное значение.
Случайные величины обозначают греческими буквами, снабжая их при необходимости индексами: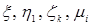 
и т. д., а их возможные значения - строчными латинскими буквами: 
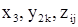. Иногда случайные величины обозначают прописными латинскими буквами, снабжая их при необходимости индексами, например, X, Y1, Zij.
|
|
|
Наиболее полным, исчерпывающим описанием случайной величины является ее закон распределения.
Определение. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Общим законом распределения, присущим всем случайным величинам, является функция распределения.
Определение. Функцией распределения (вероятностей) случайной величины ξ называют функцию Fξ (x), определенную на всей числовой оси, значение которой в точке х равно вероятности события
{ξ < x}, т. е.
F(x) = P{ξ < x}.
Функцию распределения случайной величины ξ будем обозначают Fξ (x) или F(x), если ясно, о распределении какой случайной величины идет речь. В случаях, когда известна функция распределения Fξ (x), принято говорить, что задан закон распределения случайной величины ξ.
Функция распределения F(x) случайной величины ξ удовлетворяет следующим свойствам:
1. Значения функции распределения заключены между нулем и единицей (включительно), т. е.
0 ≤ F(x) ≤ 1.
2. Функция распределения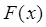 
– неубывающая функция. Это означает, что F(x1)≤ F(x2) при x1 < x2 для любых значений x1, x2 
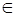R.
3. Вероятность попадания случайной величины ξ в промежуток [a, b) равна разности значений функции распределения на концах этого промежутка, т. е.
P{a ≤ ξ < b} = F(b) – F(a).
4. F (+ ∞ ) =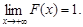 
5. F (- ∞ ) = 
6. Функция распределения 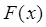непрерывна слева в каждой точке, т. е.
С точки зрения устройства множества значений, которые принимают случайные величины, из них можно естественным образом выделить два класса: дискретные и непрерывные случайные величины.
|
|
|
Определение. Случайная величина 
называется дискретной, если множество ее возможных значений конечно или счетно, т. е. может быть занумеровано натуральными числами.
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Простейшей формой задания закона распределения дискретной случайной величины является табличный (матричный) в виде ряда распределения. В связи с этим введем следующее определение.
Определение. Рядом распределения (вероятностей) дискретной случайной величины ξ называют таблицу, состоящую из двух строк: в верхней строке перечислены (как правило в порядке возрастания) все возможные значения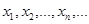 
случайной величины, а в нижней строке – соответствующие вероятности 
с которыми эти значения принимаются.
| ξ | х1 | х2 | … | хn |
| р | p1 | p2 | … | pn |
Для проверки правильности таблицы ряда распределения рекомендуется просуммировать вероятности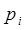 
. В силу свойства нормировки эта сумма должна быть равна единице:
При решении многих задач нет необходимости указывать закон распределения случайной величины, а достаточно задать лишь некоторые (неслучайные) числа, которые в сжатом виде характеризуют случайную величину. В теории вероятностей такие числа называют числовыми характеристиками случайной величины. Важнейшими среди названных характеристик являются математическое ожидание, задающее «центральное» значение случайной величине, и дисперсия, характеризующая «разброс» значений случайной величины вокруг её математического ожидания.
Математическое ожидание дискретной случайной величины. Свойства математического ожидания
Пусть дискретная случайная величина ξ задана рядом распределения
| ξ | х1 | х2 | … | хn |
| р | p1 | p2 | … | pn |
где 
x 
, 
и 
.
Определение. Математическим ожиданием Μ (ξ ) или средним значением дискретной случайной величины ξ, заданной на вероятностном пространстве (Ω, U, P), называется сумма произведений всех её возможных значений на соответствующие вероятности, т. е.
. Вероятностный смысл математического ожидания Μ (ξ ) состоит в том, что оно является средним значением случайной величины.
|
|
|
Пример. Найти математическое ожидание дискретной случайной величины, закон распределения которой задан таблицей
| ξ | |||||
| р | 0, 1 | 0, 2 | 0, 4 | 0, 2 | 0, 1 |
Решение. В соответствии с формулой находим
.
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно этой же постоянной величине, т. е.
М(С)=С, где С=const.
2. Постоянный множитель С можно выносить за знак математического ожидания, т. е.
.
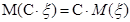3. Математическое ожидание алгебраической суммы двух случайных величин равно сумме их математических ожиданий, т. е.
М(ξ 
η )=М(ξ ) М(η ).
4. Математическое ожидание произведения двух независимых случайных величин ξ и η равно произведению их математических ожиданий, т. е.
.
5. Математическое ожидание отклонения случайной величины от её математического ожидания равно нулю:
М[ξ -М(ξ )] = 0.
Пример. Найти математическое ожидание случайной величиныη =7–2ξ, если М(ξ )=3.
Решение. Воспользуемся свойствами математического ожидания и найдём
.
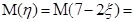
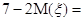
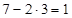Дисперсия и среднее квадратическое отклонение дискретной случайной величины. Свойства дисперсии
Рассмотрим следующую числовую характеристику случайных величин. Определение. Дисперсией D(ξ ) случайной величины ξ называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания М(ξ ):
D(ξ )=M[ξ - M(ξ )]2.
Дисперсия является мерой «разброса» или рассеивания значений случайной величины около её математического ожидания. Если воспользоваться свойствами математического ожидания, то правую часть можно привести к следующему виду:
|
|
|
.
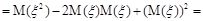
Отсюда следует, что
D(ξ )= М(ξ 2)–(М (ξ ))2.
Таким образом, дисперсия D(ξ ) случайной величины ξ равна разности между М(ξ 2) средним значением (математическим ожиданием) квадрата случайной величины и (М(ξ ))2 – квадратом её среднего значения. Эта формула является удобной для практического вычисления дисперсии. Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину 
.
Определение. Средним квадратическим отклонением или стандартным отклонением σ (ξ ) случайной величины ξ называется квадратный корень из её дисперсии:
σ (ξ ) = 
. (7. 15)
Величина σ (ξ ) характеризует, как тесно группируются значения ξ вокруг среднего значения.
Пример. Дискретная случайная величина ξ задана законом распределения
| ξ | |||||
| р | 0, 2 | 0, 3 | 0, 3 | 0, 1 | 0, 1 |
Найти M(ξ ), D(ξ ) и σ (ξ ).
Решение. Так как случайная величина ξ принимает конечное множество значений, то её математическое ожидание находим по формуле
.
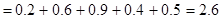Найдём закон распределения ξ 2
| ξ 2 | |||||
| р | 0, 2 | 0, 3 | 0, 3 | 0, 1 | 0, 1 |
и математическое ожидание величины ξ 2 :
8, 2.
Для нахождения дисперсии D(ξ )воспользуемся формулой
D(ξ ) = М(ξ 2)–(М (ξ ))2 = 8. 2-(2. 6)2=8. 2-6. 76=1. 46.
Тогда
σ (ξ ) = = 
.
При построении математической модели задачи принятия решений в условиях риска, помимо задания функции реализации, необходимо знание дополнительной информации о вероятностях различных состояний среды. Эта дополнительная информация может быть представлена в виде вероятностной меры на множестве состояний среды Y. Если множество состояний среды конечно, то вероятностную меру можно представить в виде вероятностного вектора y={y1, y2, …, yn}, где
yj – вероятность наступления состояния j=1, 2, …, n,
.
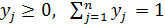Оценочная структура задается в виде оценочной функции.
Таким образом, в задаче принятия решений в условиях риска имеем:
· Целевую функцию, представленную в виде матрицы выигрышей ||aij||;
· Вероятностный вектор y={y1, y2, …, yn}.
Эта задача рассматривается в рамках теории игр как игры с природой.
Матрица выигрышей задается в виде:
|
Альтернативы |
Состояние среды | ||||
| y1 | … | yj | … | yn | |
| a11 | … | a1j | … | a1n | |
| … | … | … | … | … | … |
| i | ai1 | … | aij | … | ain |
| … | … | … | … | … | … |
| m | am1 | … | amj | … | amn |
|
|
|
Выбирая альтернативу i, принимающий решение знает, что получит один из выигрышей ai1, …, amj, …, amn с соответствующими вероятностями y1, …, yj, …, yn.
Тогда при выборе альтернативы i, исходом для лица, принимающего решение, явится случайная величина ξ i, заданная в соответствии с теорией игр, следующей матрицей:
.
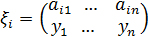Сравнение различных альтернатив i1, i2 в этом случае состоит в сравнении случайных величин ξ i1, ξ i2.
Рассмотрим пример.
Выбор варианта товара для продажи.
Фирма А может выставить на продажу один из товаров Т1 или Т2, а фирма В – один из товаров П1, П2, П3. Товары Т1 и П1 являются конкурирующими (допустим, лимонад и квас), товары Т1 и П3 являются дополнительными (допустим, чипсы и сухарики), остальные товары нейтральны. Прибыль фирмы А будет зависеть от сочетания товаров, выставленных на продажу обеими фирмами и выражается в денежных единицах следующей матрицей:
| П1 | П2 | П3 | |
| Т1 | |||
| Т2 |
Известно также, что фирма В выставляет товар П3 в три раза реже, чем товар П1 и в четыре раза реже, чем товар П2.
Какой товар для продажи выгоднее выставить фирме А?
Будем рассматривать задачу принятия решений для фирмы А. Приведенная таблица будет представлять собой таблицу выигрышей, а состояние среды будут определять товары, выставленные на продажу фирмой В. Вероятности этих состояний найдем из условий задачи. Примем за х долю случаев, когда на продажу выставляется товар П3. Тогда доля случаев выставления на продажу товара П1 будет равна 3х, а товара П2 – 4х. Так как сумма вероятностей всех состояний должна быть равна единице,
х + 3х + 4х = 1, откуда х = 1/8, и вероятности состояния среды П1 = 3/8, П2 = 4/8, П3 = 1/8. Получаем следующую матрицу задачи принятия решений:
| П1 3/8 | П2 4/8 | П3 1/8 | |
| Т1 | |||
| Т2 |
Для сравнения альтернатив мы должны сравнить между собой две случайные величины, определяемые возможными значениями с соответствующими вероятностями. Для этого рассмотрим в качестве оценки характеристику случайной величины ξ, которая определяет ее среднее значение – математическое ожидание Мξ. Рассчитаем эти величины для альтернатив Т1 и Т2.
Мξ 1 = 8·3/8 + 18·4/8 + 40·1/8 = 17;
Мξ 2 = 18·3/8 + 15·4/8 + 14·1/8 = 16.
Возьмем в качестве критерия альтернативу, которая максимизирует выигрыш, это будет альтернатива Т1.
Проанализируем полученный результат. Действительно ли альтернатива Т1 лучше, чем альтернатива Т2? Поскольку математическое ожидание случайной величины есть характеристика, к которой приближается среднее значение этой случайной величины при достаточно большом числе испытаний, математическое ожидание выигрыша будет характеризовать средний выигрыш при многократном повторении игры. Всегда ли нужно в таком случае ориентироваться на такую характеристику при оценке критерия?
Такой выбор критерия действительно оправдан, когда игра повторяется многократно, а как быть, если мы имеем дело с единичным испытанием?
На первый взгляд действительно выигрыш 17 денежных единиц лучше, чем 16. Но выбрав альтернативу Т1, можно получить 8, 18 или 40 денежных единиц, а выбрав альтернативу Т2, получить выигрыш 18, 15 или 14 денежных единиц. Рассмотрим таблицу отклонений для возможных выигрышей от их ожидаемых значений, вероятностей этих отклонений и ожидаемые значения выигрышей для двух альтернатив:
| П1 3/8 | П2 4/8 | П3 1/8 | Мξ | |
| Т1 | -9 | |||
| Т2 | -1 | -2 |
Видим, что ожидаемые значения альтернатив близки, а вот отклонения возможных значений выигрыша ведут себя по-разному – в альтернативе Т1 отклонения могут быть велики по сравнению с самим ожидаемым выигрышем, а в альтернативе Т2 эти отклонения невелики.
Это наблюдение приводит к следующему выводу: в задаче принятия решений в условиях риска критерий ожидаемого среднего выигрыша не может считаться адекватным, и его необходимо преобразовать с учетом возможных отклонений случайной величины от своего среднего значения.
В качестве меры разброса случайной величины от своего среднего в теории вероятностей используется дисперсия случайной величины Dξ, имеющая размерность квадрата единиц ее измерения и среднеквадратическое отклонение (СКО) 
, имеющее те же единицы измерения, что и сама случайная величина. Поэтому, в силу одинаковых единиц измерения, в задаче принятия решений в условиях риска рассматривается среднеквадратическое отклонение случайной величины s.
Таким образом, выбор альтернативы i в задаче принятия решений в условиях риска вызывает необходимость оценки случайной величины ξ i. Для оценки случайной величины удобно использовать ее числовые характеристики – математическое ожидание и среднеквадратическое отклонение в виде пары чисел (Mi, si), где Mi = Мξ i - ожидаемый выигрыш,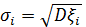 
- показатель риска. Используя эти характеристики, можно построить критерий сравнения двух альтернатив. В сущности эта задача представляет собой задачу двухкритериальной оптимизации, в которой в качестве частных критериев выступают М и s.
|
|
|
