 |
Метод обобщенного критерия.
|
|
|
|
Рассмотрим метод соединения двух критериев в один обобщенный критерий.
Построим обобщенный критерий в виде:
 ,
,
где l - некоторая постоянная величина. Этот критерий представляет собой взвешенную сумму частных критериев М и s с весами 1 и (-l).
При l > 0 оценка случайной величины с помощью полученного обобщенного критерия будет меньше ее среднего значения. Этот критерий относится к осторожному, не склонному к риску поведению.
При l < 0 оценка случайной величины будет больше ее среднего значения. В этом случае критерий характеризует поведение, склонное к риску.
При l = 0 оценка случайной величины совпадает со средним значением. Это является характеристикой поведения, безразличного к риску.
Рассмотрим случай поведения, не склонного к риску, l > 0.
В этом случае увеличение обобщенного критерия q будет происходить как за счет увеличения математического ожидания выигрыша М, так и за счет уменьшения его разброса s. Человек, не склонный к риску, используя критерий l > 0, стремится к увеличению ожидаемого выигрыша и уменьшению риска отклонения от него. Показатель l характеризует отношение лица, принимающего решение, к риску. Чем больше он выбирает значение l, тем в большей степени он не склонен к риску. Таким образом, значение величины l можно рассматривать как субъективный показатель меры несклонности к риску, или осторожности.
Учет риска в обобщенном критерии происходит следующим образом. В зависимости от несклонности или склонности к риску, ожидаемый выигрыш уменьшается или увеличивается на величину, равную произведению показателя риска s, который является объективной характеристикой меры риска, на субъективный показатель l, который определяет отношение к риску человека, принимающего решение.
|
|
|
Насколько по величине субъективного показателя l можно судить о мере склонности к риску? Для оценки этой меры воспользуемся неравенством Чебышёва, рассматриваемым в курсе теории вероятностей.
Рассмотрим случай, когда принимающий решение не склонен к риску. Критерием оценки случайной величины ξ является обобщенный критерий  . Неблагоприятной для лица, принимающего решение, является ситуация, когда ξ < M - ls. Оценим вероятность этого события.
. Неблагоприятной для лица, принимающего решение, является ситуация, когда ξ < M - ls. Оценим вероятность этого события.
В этом случае выполняется неравенство M – ξ > ls, отсюда |ξ – M| > ls. В силу неравенства Чебышёва, вероятность события |ξ – M| > ls меньше, чем
Dξ /(ls)2 = s2/(l2s2) = 1/l2.
Это означает, что вероятность того, что случайная величина ξ примет значение, меньшее ее оценки М - ls, не превосходит 1/l2. Противоположное событие, вероятность того, что случайная величина ξ примет значение, не меньшее ее оценки М - ls, будет не меньше, чем 1 - 1/l2.
Например, если l = 3, то вероятность того, что случайная величина будет не меньше, чем оценка М - ls, будет не меньше, чем 1 – 1/9 = 0, 888…, то есть, почти 90%. В этом случае можно считать, что риск не высок. Тогда значение l = 3 соответствует достаточно большой степени несклонности к риску, или осторожности.
Теперь рассмотрим процедуру оценки альтернатив по обобщенному критерию q.
Рассмотрим случай несклонности к риску. Тогда принимающий решение стремится увеличить ожидаемый выигрыш и уменьшить риск, критерий М в таком случае будет позитивным, а критерий s - негативным. Пусть задано некоторое множество альтернатив (аi), каждая альтернатива характеризуется парой показателей (Mi, si). Выберем какие-нибудь две альтернативы 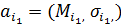 ,
,  . Обобщенные критерии для этих альтернатив
. Обобщенные критерии для этих альтернатив 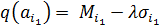 ,
,  . Возможны два случая.
. Возможны два случая.
1). Альтернативы сравнимы по Парето. Пусть  по Парето. Тогда
по Парето. Тогда 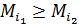 ,
,  , при этом хотя бы одно неравенство строгое. Получим, что
, при этом хотя бы одно неравенство строгое. Получим, что
|
|
|
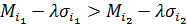 , или
, или
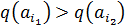 .
.
В результате, в этом случае получили, что независимо от меры несклонности к риску лица, принимающего решение (то есть от показателя l > 0), альтернатива  более предпочтительна, чем альтернатива
более предпочтительна, чем альтернатива  .
.
2). Альтернативы не сравнимы по Парето.
Например, пусть 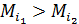 ,
,  . Больший ожидаемый выигрыш всегда сопровождается большим риском. Условие
. Больший ожидаемый выигрыш всегда сопровождается большим риском. Условие 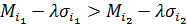 равносильно тому, что
равносильно тому, что  .
.
Тогда в этом случае
альтернатива  более предпочтительна, чем альтернатива
более предпочтительна, чем альтернатива  , если
, если  ,
,
альтернатива  более предпочтительна, чем альтернатива
более предпочтительна, чем альтернатива  , если
, если  .
.
Введем следующие обозначения:
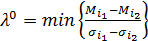 ,
, 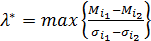 .
.
Операторы min и max распространяются на такие пары индексов (i1, i2), для которых альтернативы  ,
,  оптимальны по Парето и
оптимальны по Парето и 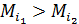 , следовательно
, следовательно  .
.
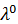 назовем нижней границей несклонности к риску,
назовем нижней границей несклонности к риску,
 - верхней границей несклонности к риску.
- верхней границей несклонности к риску.
При этом всегда  . Для лица, не склонного к риску получаем правило.
. Для лица, не склонного к риску получаем правило.
Правило. 1. Если у принимающего решение его субъективный показатель несклонности к риску меньше нижней границы l<  , то для него ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию q совпадает с ранжированием по показателю ожидаемого выигрыша М, и предпочтительней будет альтернатива, для которой ожидаемый выигрыш больше.
, то для него ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию q совпадает с ранжированием по показателю ожидаемого выигрыша М, и предпочтительней будет альтернатива, для которой ожидаемый выигрыш больше.
2. Ели у принимающего решение его субъективный показатель несклонности к риску больше верхней границы l > 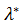 , то для него ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию q совпадает с ранжированием по показателю риска s, и прдпочтительней будет альтернатива, для которой меньше риск.
, то для него ранжирование множества Парето-оптимальных альтернатив по обобщенному критерию q совпадает с ранжированием по показателю риска s, и прдпочтительней будет альтернатива, для которой меньше риск.
Следовательно, в задаче принятия решений в условиях риска применение обобщенного критерия сводит проблему нахождения оптимального решения к проблеме установления для лица, принимающего решение, его меры склонности или несклонности к риску. Таким образом, появляется проблема не математического, а псхологического свойства, дающего характеристику субъективных качеств принимающих решение лиц.
Недостатком метода обобщенного критерия является предположение постоянства меры несконности к риску для лица, принимающего решение, из которого следует постоянство локального коэффициента замещения между критериями М и s. На самом деле мера склонности к риску у человека непостоянна и зачастую зависит от величины ожидаемого выигрыша и степени риска. Примером несклонности к риску является наличие большого количества разного вида страхования, в которых участвует значительная часть населения. Пример склонности к риску – большое количество любителей участвовать в лотереях, в которых стоимость билетов всегда превышает ожидаемый выигрыш.
|
|
|
Для деловых людей в сфере предпринимательства, как правило, характерна несклонность к риску. Однако в некоторых случаях они соглашаются участвовать в мероприятиях, в которых ожидаемый доход меньше доли вложенного капитала, если сами доходы в некоторых благоприятных условиях могут быть очень велики. Такое поведение объясняют сменой целевых установок, когда цель максимизации прибыли сменяется целью пробиться к следующему, более высокому уровню доходов, которая достигается только при большой степени риска.
|
|
|


