 |
Метод, основанный на отношении доминирования по Парето.
|
|
|
|
Метод, основанный на отношении доминирования по Парето.
Будем считать, что принимающий решение не склонен к риску, при этом критерий М ожидаемого выигрыша будет позитивным, а критерий s - негативным.
Пусть задано некоторое множество альтернатив (аi), каждая альтернатива характеризуется парой показателей (Mi, si). Требуется выбрать оптимальную альтернативу на заданном множестве.
Каждую альтернативу можно изобразить на координатной плоскости (М, s), получится следующая картинка:
Условие доминирования по Парето 
предполагает, что для альтернативы 1 получается такой же, или больший, ожидаемый выигрыш, что и для альтернативы 2, но с меньшим, или таким же, риском. Для данного примера, изображенного на рисунке, множество Парето-оптимальных альтернатив есть {a1, a4, a7, a8}. Выбор оптимальной альтернативы будет производится из данного множества. Возможны два подхода.
Первый подход основан на том, что формальный анализ заканчивается указанием множества Парето-оптимальных альтернатив, а выбор оптимального решения производит лицо, принимающее решение на основе неформальных дополнительных соображений.
Второй подход заключается в применении процедур сужения множества Парето-оптимальных альтернатив.
1). Субоптимизация. Выбирается один критерий, и назначаются нижние границы по остальным критериям. В данной задаче в качестве критерия служит ожидаемый выигрыш, поэтому субоптимизация проводится таким образом. Назначается нижняя граница по критерию и оптимизируется оставшийся критерий s. Оптимизация критерия s в данном случае состоит в его минимизации.
Например, если взять за нижнюю границу критерия ожидаемого выигрыша значение М6, то оптимальной будет альтернатива а4, поскольку среди всех альтернатив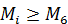 
, она менее рискованна.
|
|
|
2). Лексикографическая оптимизация. Применение этого метода оптимизации предполагает процедуру упорядочения критериев по относительной важности.
Пусть критерий М выбран как важнейший. В данной задаче максимальное значение по критерию М имеет альтернатива а8, следовательно, она и будет оптимальной. Недостаток метода лексикографической оптимизации состоит в том, что учитывается фактически только один важнейший критерий. Этот недостаток вытекает из необходимости введения жесткого упорядочения (приоритета) критериев.
Метод последовательных уступок.
Жесткость приоритетов можно ослабить следующим образом. Назначается некотрая уступка d1 по важнейшему критерию. На первом шаге отбираются альтернативы, оценка которых по важнейшему критерию отличается от максимальной не более чем на эту уступку d1. Далее делается уступка d2 для второго по важности критерия. Среди оставшихся после первого шага альтернатив выбираются такие, оценка которых по второму критерию будет отличаться от максимальной не более, чем на уступку d2 и так далее по всем оставшимся критериям. Для данной задачи для критерия ожидаемого выигрыша в качестве уступки взята величина d1, обозначенная на рисунке. В результате первого шага будут выбраны альтернативы {a7, a8, a9}. Среди этих альтернатив наилучшей по второму критерию является альтернатива a7. Она и будет оптимальной альтернативой данной задачи. Поведем итог. Незначительно снизив требования по критерию М, мы значительно улучшили оценку по критерию s. Следовательно, некоторое уменьшение ожидаемого выигрыша привело к существенному снижению риска.
Недостаток метода последовательных уступок заключается в том, что необходимо получение дополнительной информации от лица, принимающего решение, о величине уступки по каждому критерию, кроме последнего.
|
|
|
Пример.
Выбор варианта производимого товара.
Фирма может производить продукцию одного из шести видов:
З - зонты, К – куртки, П – плащи, С – сумки, Т – туфли, Ш – шляпы. Необходимо принять решение, какой из этих товаров выпускать в течение предстоящего летнего сезона. Прибыль фирмы зависит от того, каким будет лето. Рассматриваются три варианта – Д - дождливое лето, Ж - жаркое или У - умеренное. Ожидания прибыли определяются в соответствии с заданной матрицей альтернатив. Выбор какого варианты выпуска изделий будет оптимальным?
Если дополнительная информация о состоянии среды неизвестна, то задача превращается в задачу принятия решений в условиях неопределенности. Решение ее проводится ранее рассмотренными методами принятия какой-либо гипотезы и поведении среды. Если же известна какая-либо информация о вероятностях наступления определенных состояний среды, в данном случае о прогнозах погоды на лето, тогда имеем задачу принятия решений в условиях риска. Допустим, в данной задаче из статистических наблюдений известно вероятность наступления дождливого, жаркого и умеренного лета, которая равна соответственно 0, 2: 0, 5; 0, 3.
Таким образом, имеем следующие данные.
Матрица выигрышей:
| Д | Ж | У | |
| З | |||
| К | |||
| П | |||
| С | |||
| Т | |||
| Ш |
Учет состояния среды:
| Д р1=0, 2 | Ж р2=0, 5 | У р3=0, 3 | |
| З | |||
| К | |||
| П | |||
| С | |||
| Т | |||
| Ш |
Ожидаемые выигрыши для шести альтернатив найдем как математические ожидания случайной величины, заданной последней таблицей.
МЗ = 80·0, 2 + 60·0, 5 + 40·0, 3 = 58,
МК = 70·0, 2 + 40·0, 5 + 80·0, 3 = 58,
МП =70·0, 2 + 50·0, 5 + 60·0, 3 = 57,
МС = 50·0, 2 + 50·0, 5 + 70·0, 3 = 56,
МТ = 75·0, 2 + 50·0, 5 + 50·0, 3 = 55,
МШ = 35·0, 2 + 75·0, 5 + 60·0, 3 = 62, 5.
Определим дисперсии случайных величин ξ З, ξ К, ξ П, ξ С, ξ Т, ξ Ш, используя свойство дисперсии
D(ξ )= М(ξ 2)–(М (ξ ))2.
Получим:
Dξ З = 6400·0, 2 + 3600·0, 5 + 1600·0, 3 - 582 = 196,
Dξ К = 4900·0, 2 + 1600·0, 5 + 6400·0, 3 - 582 = 336,
Dξ П = 4900·0, 2 + 2500·0, 5 + 3600·0, 3 - 572 = 61,
Dξ С = 2500·0, 2 + 2500·0, 5 + 4900·0, 3 - 562 = 84,
Dξ Т = 5625·0, 2 + 2500·0, 5 + 2500·0, 3 - 552 = 100,
Dξ Ш = 1225·0, 2 + 5625·0, 5 + 3600·0, 3 – 62, 52 = 231, 5.
Определим среднеквадратические отклонения:
|
|
|
, 
, 
,
, 
, 
.
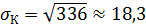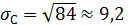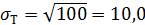Запишем критерии М и s в таблицу:
| М | s | |
| З | 14, 0 | |
| К | 18, 3 | |
| П | 7, 8 | |
| С | 9, 2 | |
| Т | 10, 0 | |
| Ш | 62, 5 | 15, 2 |
Обозначив на плоскости (М, s) оценки альтернатив, получим рисунок
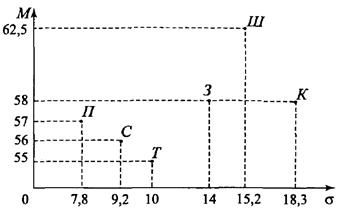
Согласно рисунку, получим Парето-оптимальное множество {З, П, Ш}. Выбор оптимальной альтернативы определяется из этого множества. Сужение Парето-оптимального множества возможно при наличии дополнительной информации относительно соотношения критериев М и s. Например, такое сужение можно производить рассмотренными ранее методами - субоптимизации или лексикографической оптимизации.
Будем сейчас искать оптимальное решение методом обобщенного критерия q.
Найдем значения q для альтернатив нашей задачи.
q(З) = 58 - 14l, q(С) = 56 – 9, 2l, q(К) = 58 – 18, 3l,
q(Т) = 55 - 10l, q(П) = 57 – 7, 8l, q(Ш) = 62, 5 – 15, 2l.
Для того, чтобы ранжировать полученное Парето-оптимальное множество {З, П, Ш} по обобщенному критерию q, найдем нижнюю и верхнюю границы меры несклонности к риску. Получим:
, 
, 
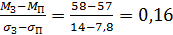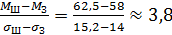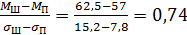
Тогда
,
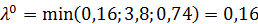Таким образом, интервал значений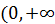 
) разбивается на три интервала по оценке склонности к риску:
(0; 0, 16) – зона малой несклонности к риску, или зона малой осторожности;
(3, 8; 
) - зона большой несклонности к риску, или зона большой осторожности;
[0, 16; 3, 8] – зона неопределенности
В соответствии с выведенным правилом, имеем:
1) Если l - мера несклонности к риску лица, принимающего решение, заключена в интервале (0; 0, 16), то в этом случае ранжирование множества Парето-оптимальных альтернатив совпадает с их ранжированием по величине ожидаемого выигрыша: Ш предпочтительнее З, З предпочтительнее П.
2) Если для лица, принимающего решение мера несклонности к риску l > 3, 8, то в этом случае ранжирование множества Парето-оптимальных альтернатив совпадает с их ранжированием по показателю риска. Альтернатива П предпочтительнее альтернативы З, З предпочтительнее Ш, оптимальной будет альтернатива П.
3) Случай, если мера несклонности принимающего решение попадет в зону неопределенности. Например, пусть l=2.
|
|
|
Тогда q(З) = 58 - 14·2=30, q(П) = 57 – 7, 8·2=41, q(Ш) = 62, 5 – 15, 2·2=32, 1.
Тогда ранжирование дает такой результат: альтернатива П предпочтительнее альтернативы Ш, Ш предпочтительнее З. В этом случае для пары (З, Ш) предпочтение будет определяться величиной ожидаемого выигрыша, а для пары (П, Ш) – величиной риска.
|
|
|
