3.3 Критерий ожидаемой полезности

Исходом в задаче принятия решений в условиях риска является некоторая случайная величина, поэтому при сравнении альтернатив сравниваются соответствующие этим исходам случайные величины. Рассмотренный ранее метод сравнения альтернатив состоит из двух последовательных шагом. Сначала случайная величина ξ характреризуется векторной оценкой (М, s), включающей ее математическое ожидание и среднеквадратическое отклонение. Затем вводится некоторый способ сравнения полученных векторных оценок. Метод построения обобщенного критерия «переводит» векторную оценку (М, s) в скалярную оценку q.

В результате этого получаем соответствие ξ , в котором случайная величина ξ описывается единственным числом q(ξ ). Это число выражает полезность в процессе принятия решения. При этом сравнение по предпочтительности двух случайных величин ξ ₁ и ξ ₂ происходит путем сравнения чисел q(ξ ₁) и q(ξ ₂). Это дает возможность сравнения любых двух альтернатив в задаче принятия решений в условиях риска, а затем и нахождения оптимального решения.

Недостатки метода состоят в следующем.

Во-первых, описание эффективности с помощью ожидаемого выигрыша как математического ожидания случайной величины и риска с помощью среднеквадратического отклонения, является не единственно возможным.

Во-вторых, при построении обобщенного критерия q требуется задание дополнительной информации о соотношении этих критериев друг с другом. Поэтому в теории принятия решений применяются и другие методы.

Важную роль при этом играет метод, основанный на построении функции полезности.

Сделаем вводные замечания. Случайную величину ,  

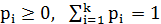 будем рассматривать как лотерею с выигрышами      

x₁, …, x_k, в которой p_i – доля билетов с выигрышами    x_i (i=1, …, k). При этом любые две лотереи, выигрыши в которых содержатся в одинаковой пропорции, считаются эквивалентными (равноценными).

Определение Детерминированным денежным эквивалентом лотереи ξ (ДДЭ ξ ) называется денежная сумма х, которая для принимающего решение эквивалентна его участию в этой лотерее.

Таким образом, если ДДЭ лотереи ξ равен х, то принимающему решение безразлично – получить денежную сумму х или участвовать в лотерее ξ.

Чтобы найти ДДЭ произвольной денежной лотереи, нужно научиться находить ДДЭ простых лотерей, то есть, лотерей с двумя выигрышами. Всякая простая лотерея с выигрышами а и А, где а < A, может быть записана в виде , .

Число р называется параметром простой лотереи. Кривая, которая устанавливает соответствие между параметрами простых лотерей и ДДЭ этих лотерей, называется кривой денежных эквивалентов. При построении кривой денежных эквивалентов высказывается предположение, что принимающий решение указывает свой субъективный детерминированный денежный эквивалент для некоторых простых лотерей. Построим кривую денежных эквивалентов в плоскости, где по оси абсцисс откладываются деньги в некоторых денежных единицах, а по оси ординат – параметр простой лотереи р  Кривая денежных эквивалентов строится из точек с координатами (х_р, р), где х_р – ДДЭ простой лотерии ξ _р, а р – параметр простой лотереи ξ _р.

При р = 0 имеем простую лотерею 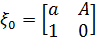, то есть такую лотерею, в которй доля выигрышей равна 100%, ДДЭ такой лотереи будет равен а.

При р = 1 имеем простую лотерею с ДДЭ равным А.

Кривая денежных эквивалентов всегда будет проходить через точки (а, 0) и (А, 1).

Математическое ожидание выигрыша в простой лотерее  , равно 

М

Итак, получили, что Мξ _р является линейной функцией переменной р, а значит, графиком этой функции будет прямая. Так как при р = 0 Мξ ₀ = а, а при р = 1 Мξ ₁ = А, эта прямая проходит через точки (а, 0) и (А, 1), как и любая кривая денежных эквивалентов.

Рассмотрим теперь простую лотерею с параметром р= 0, 5. В такой лотерее выигрыши а и А равновероятны, такие лотереи иногда называют лотереи 50 - 50.

.

В соответствии с данным ранее определением, ДДЭ лотереи  – это денежная сумма х_{0, 5}, которая для лица, принимающего решение, эквивалентна (равноценна) его участию в лотерее. Какова может быть величина х_{0, 5}? Например, возьмем простую лотерею с выигрышами 10 денежных единиц и 100 денежных единиц. Участие в такой лотерее обычно оценивается в сумму 20-30 денежных единиц, суммой, значительно меньшей, чем математическое ожидание выигрыша в такой лотерее, которое в данном случае равно 55 денежных единиц. ДДЭ этой лотереи не может быть ниже 10. Следовательно, 10 < х_{0, 5} < 55. Тогда в общем случае а < х_{0, 5} < Мξ _{0, 5}. Тогда точка (х_{0, 5}; 0, 5) лежит на горизонтальной прямой р = 0, 5 между точками пересечения с прямой  х = а и прямой l, соединяющей точки (а; 0) и (А; 1), как показано на рисунке.

Принимающий решение теперь должен задать ДДЭ простых лотере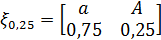й

 и ,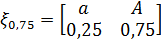

то есть, задать х_{0, 25} и  х_{0, 75}.

Повторив рассуждения, приведенные для нахождения точки х_{0, 5}, получим неравенства:            а < х_{0, 25} < х_{0, 5}, х_{0, 5}< х_{0, 75} < А.

Получим на кривой денежных эквивалентов пять точек: (а; 0), (А; 1), (х_{0, 25}; 0, 25), (х_{0, 5}; 0, 5), (х_{0, 75}; 0, 75). Три последние точки получаются путем опроса принимающего решения. Через эти пять точек проводим гладкую кривую и получаем в результате эмпирическую кривую денежных эквивалентов. Приведенный способ построения кривой денежных эквивалентов называется способом пяти точек.

 

Рассмотрим следующие замечания.

1. Предположим, что ДДЭ простой лотереи 50-50 уже установлен, то есть указана точка х_{0, 5}. Поскольку точка р = 0, 25 является серединой отрезка с концами р = 0 и р = 0, 5, ДДЭ лотереи с параметром р = 0, 25 будет равен ДДЭ лотереи 50-50 с выигрышами а и х_{0, 5}, а именно, 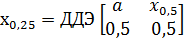, и аналогично .

Получаем, что для построения кривой денежных эквивалентов достаточно уметь находить ДДЭ некоторых лотерей 50-50, выигрыши которых находятся в интервале (а; А). Количество эмпирических точек на кривой при необходимости можно увеличивать.

2. Характерным свойством эмпирической кривой денежных эквивалентов является тот факт, что при любом значении параметра р простой лотереи ξ _р

ДДЭ ξ _р < M ξ _р.

Данное неравенство отражает несклонность принимающего решение к риску – участие в лотерее ξ _р оценивается им суммой, меньшей ожидаемого выигрыша в этой лотерее.

Определение функции полезности денежного критерия.

Предположим, что имеется построенная кривая денежных эквивалентов простых лотерей с выигрышами а и А. Пусть теперь х есть ДДЭ простой лотереи с параметром р.

Тогда величина u(x) = p называется полезностью денежной суммы x. Таким образом, по определению выполняется следующая равносильность:

u(x) = p ДДЭ ξ _р = x.

Функция u(x) называется эмпирической функцией полезности денежного критерия, или функцией полезности денег.

Имеется следующее правило.

Функция полезности денежного критерия есть функция u(x), графиком которой служит кривая денежных эквивалентов.

Будем считать, что выполнены два условия.

1) При небольшом изменении параметра р простой лотереи ее ДДЭ изменяется незначительно. Это условие формально означает, что функция  является непрерывной.

2) Если р₁ < p₂, то ДДЭ ξ _р1 < ДДЭ ξ _р2с. Условие формально означает, что функция  является монотонно возрастающей.

Тогда, при этих предположениях существует обратная функция, причем она является также непрерывной и строго монотонной. В данном случае обратной функцией является функция полезности u(x). Следовательно, при указанных условиях 1) и 2) функция полезности u(x) существует, является непрерывной и строго монотонно возрастающей.

Поскольку в лотерее ξ _р число р указывает долю содержащихся в ней «удачных» билетов, имеющих выигрыш А, определим следующее правило. a

Правило

Полезность денежной суммы х, где а ≤ х ≤ А, совпадает с долей «удачных» билетов в простой лотерее с выигрышами а и А, участие в которой эквивалентно для принимающего решение получению денежной суммы х.

Замечания.

1) Поскольку функция полезности строится путем нахождения ДДЭ лотерей, она носит субъективный характер.

2) Бессмысленным являетс вопрос типа: «Чему равна полезность тысячи долларов? ». Чтобы правильно задать такой вопрос, надо вначадле зафиксировать границы денежных выигрышей а и А. После этого для  можно рашать вопрос определения полезности функции u(x)/

3) Функция полезности u(x) определена для всех х, заключенных между а и А, то есть областью определения функции u(x) является отрезок [a, A]

4) Значения функции полезности заключены между    0 и 1,             причем u(а) = 0, u(А) = 1.

5) Функция полезности денежного критерия является монотонно возрастающей в строгом смысле, то есть условие х₁ < x₂ влечет u(х₁) < u(х₂).

6) Если лицо, принимающее решение, не склонно к риску, то его функция полезности является вогнутой, изображенной на рисунке линией а).

 

 

 

7) Если принимающий решение, склонен к риску, то его функция полезности является выпуклой, что на графике представлено кривой б). Склонность к риску проявляется в том, что принимающий решение оценивает свое участие в лотерее суммой, которая больше, чем ожидаемый выигрыш в этой лотерее ДДЭξ > Mξ.

8) Если принимающий решение безразличен к риску, то он оценивает лотерею суммой, которая равна ожидаемому выигрышу в этой лотерее, тогда график его функции полезности выражается в виде прямой, соединяющей точки (а; 0) и (А; 1), что изображено на графике прямой в).

Таким образом, степень склонности или несклонности к риску проявляется в степени выпуклости или вогнутости кривой графика функции полезности.

Один и тот же человек, принимающий решение, может менять свое отношение к риску, в зависимости от значений ожидаемого выигрыша, и на одних интервалах это отношение может быть отличным от отношения на дркгих интервалах. На следующем рисунке обозначено, что на интервале (а, а₁) принимающий решение проявляет безразличие к риску, на интервале (а₁, а₂) – склонность к риску и на интервале (а₂, А) – несклонность к риску. В соответствии с этим меняется характер выпуклости кривой графика функции полезности.

Вопросы к разделу.

1. В каком случае рассматривается задача принятия решения в условиях неопределенности?

2. Какие переменные входят в целевую функцию задачи принятия решения в условиях неопределенности?

3. Что представляет собой таблица выигрышей?

4. Какая альтернитива называется доминирующей?

5. Какая альтернитива называется доминируемой?

6. Каким образом можно упрастить платежную матрицу?

7. В чем состоит критерий Лапласа?

8. Что такое принцип недостаточного основания?

9. Какой критерий является крайне пессимистическим?

10. какой критерий является крайне оптимистическим?

11. В каком случае рассматривается задача принятия решения в условиях риска?

12. Как строится обобщенный критерий?

13. Какой критерий дает ожидаемый выигрыш?

14. Какой критерий характиризует риск?

15. Что такое функция полезности?

16. Что из себя представляет кривая функции полезности для лица, не склонного к риску?

17. Что из себя представляет кривая функции полезности для лица, склонного к риску?

18. Как выглядит график функции полезности для лица, безразличного к риску?

Литература.

1. Кравченко Т. К. Экспертная система поддержки принятия решений. Открытое образование, 2010. № 6. C. 147—156.

2. Теория и методы принятия решений: 3 - е. изд. , перераб. / О. И. Ларичев. - М. : Университетская книга, 2008.

3. Партыка Т. Л., Попов И. И. Математические методы. – М.: ФОРУМ: ИНФРА-М, 2011.

4. Розен В. В. Математические модели принятия решений в экономике. Учебное пособие. - М.: Книжный дом «Университет», Высшая школа, 2002 – 288 с.

5. Черноруцкий И. Г. Методы принятия решений. – СПб: БХВ-Петербург, 2005. – 416 с.

Дополнительная литература.

1. Р. Левин, Д. Дранг, Б. Эдельсон Практическое введение в технологию искусственного интеллекта и экспертных систем с иллюстрацией на БЭЙСИКЕ, М. Финансы и статистика, 2010

2. Экспертные системы: принципы разработки и программирование 4-е издание Джозеф Джарратано, Гари Райли, 1152 стр., с ил.; CD-ROM; . - М.: Издательский дом «Вильямс», 2006

3. Орлов А. И. Теория принятия решений. Учебное пособие. - М.: Издательство " Март", 2004. - 656 с.

4. Д. Уотеpмен. Руководство по экспеpтным системам. Москва., Миp, 1989

5. Введение в экспертные системы, 3-е издание Питер Джексон.: пер с англ. - М.: Издательский дом «Вильямс», 2001. 624 стр

6. Д. Поспелов. " Справочник по ИИ том-2".

7. Нейронные сети: полный курс, 2-е издание, Саймон Хайкин М. - " Диалектика" 2006

8. Горчаков А. А., Орлова И. В. компьютерные экономико-математические модели. – М.: Компьютер, ЮНИТИ, 1995.

9. Кофман А. Методы и модели исследования операций. – М.: Мир, 1996.

10. Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы в экономике. – М.: Издательство «Дело и сервис», 2009.

Интернет – ресурсы:

1. Информационно-справочные и поисковые системы www. gov. ru, www. fas. gov. ru

2. Информационное хранилище данных, OLAP-каталог http: //www. olap. ru/home. asp? catId=70

3. Учебный центр «Интерфейс»

 http: //www. interface. ru/fset. asp? Url=/training. htm

4. Горский П., эксперт. Авторская страница. Статьи по Системам поддержки принятия решений http: //www. pavel. gorskiy. ru/articles. html

 

 

[1] Розен В. В. Математические модели принятия решений в экономике. – М.: Высшая школа, 2002.

⇐ Предыдущая10111213141516171819

Поделиться:

Воспользуйтесь поиском по сайту: