 |
Контрольные вопросы и задания. Тема 1.5. Статика. Пространственная система сил. Тема 1.6. Центр тяжести. Сила тяжести. Точка приложения силы тяжести
|
|
|
|
Контрольные вопросы и задания
1. Запишите формулы для расчета главного вектора пространственной системы сходящихся сил.
Тема 1. 5. Пространственная система сил 57
2. Запишите формулу для расчета главного вектора пространственной системы произвольно расположенных сил.
3. Запишите формулу для расчета главного момента пространственной системы сил.
4. Запишите систему уравнений равновесия пространственной системы сил.
5. Какое из уравнений равновесия нужно использовать для определения реакции стержня R1 (рис. 7. 8)?

6. Определите главный момент системы сил (рис. 7. 9). Точка
приведения — начало координат. Координатные оси совпадают с
ребрами куба, ребро куба равно 20 см; F1 = 20 кН; F2 = 30 кН.
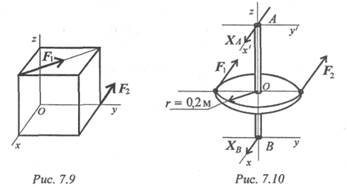
7. Определите реакцию ХВ (рис. 7. 10). Вертикальная ось со
шкивом нагружена двумя горизонтальными силами. Силы F 1 и F2 параллельны оси Ох. АО = 0, 3 м; ОB = 0, 5 м; F1 = 2 кН; F2 = 3, 5 кН.
Рекомендация. Составить уравнение моментов относительно оси Оу' в точке А.
58 Лекция 7
8. Ответьте на вопросы тестового задания.
Тема 1. 5. Статика.
Пространственная система сил

Тема 1. 5. Пространственная система сил 59

60 Лекция 8
ЛЕКЦИЯ 8
Тема 1. 6. Центр тяжести
Иметь представление о системе параллельных сил и центре системы параллельных сил, о силе тяжести и центре тяжести.
Знать методы для определения центра тяжести тела и формулы для определения положения центра тяжести плоских фигур.
|
|
|
Уметь определять положение центра тяжести простых геометрических фигур, составленных из стандартных профилей.
Сила тяжести
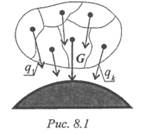
Сила тяжести — равнодействующая сил притяжения к Земле, она распределена по всему объему тела. Силы притяжения, приложенные к частицам твердого тела, образуют систему сил, линии действия которых сходятся в центре Земли (рис. 8. 1). Поскольку радиус Земли значительно больше размеров любого земного тела, силы притяжения можно считать параллельными.
Точка приложения силы тяжести
Для определения точки приложения силы тяжести (равнодействующей параллельных сил) используем теорему Вариньона о моменте равнодействующей:
Момент равнодействующей относительно оси равен алгебраической сумме моментов сил системы относительно этой оси.
Изображаем тело, составленное из некоторых частей, в пространственной системе координат (рис. 8. 2).
Тело состоит из частей, силы тяжести которых q k приложены в центрах тяжести (ЦТ) этих частей.
Пусть равнодействующая (сила тяжести всего тела) приложена в неизвестном пока центре С.
ХС, УС, ZС — координаты центра тяжести С.
Xk, Уk и Zk — координаты центров тяжести частей тела.
Тема 1. 6. Центр тяжести 61
Из теоремы Вариньона следует:

Центр тяжести однородных плоских тел
(плоских фигур)
Очень часто приходится определять центр тяжести различных плоских тел и геометрических плоских фигур сложной формы. Для плоских тел можно записать: V = Ah, где А — площадь фигуры, h — ее высота.
|
|
|
Тогда после подстановки в записанные выше формулы получим:
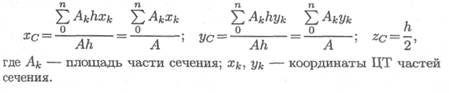
62 Лекция 8
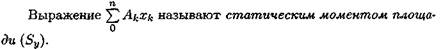
Координаты центра тяжести сечения можно выразить через статический момент:
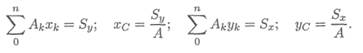
Оси, проходящие через центр тяжести, называются центральными осями. Статический момент относительно центральной оси равен нулю.
Определение координат центра тяжести
плоских фигур
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты. Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8. 3: а) — круг; б) — квадрат, прямоугольник; в) — треугольник; г) — полукруг).

При решении задач используются следующие методы:
Тема 1. 6. Центр тяжести 63
1) метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
2) метод разделения: сложные сечения разделяем на несколько
простых частей, положение центров тяжести которых легко определить;
3) метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
|
|
|


