 |
Примеры решения задач. Решение. Пример 2.Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).
|
|
|
|
Примеры решения задач
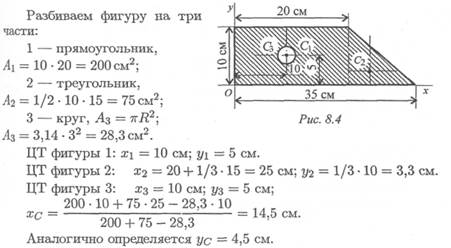
Пример 1. Определить положение центра тяжести фигуры, представленной на рис. 8. 4.
Решение
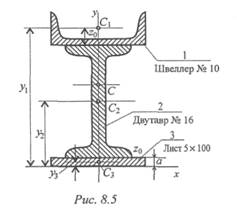
Пример 2. Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8. 5).
Примечание. Часто рамы сваривают из разных профилей, создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.
Для стандартных прокатных профилей собственные геометрические характеристики известны. Они приводятся в соответствующих стандартах.
64 Лекция 8
Решение
1. Обозначим фигуры номерами и выпишем из таблиц необходимые данные:
1 — швеллер № 10 (ГОСТ 8240-89); высота h = 100 мм; ширина полки b = 46 мм; площадь сечения А1 = 10, 9 см2;
2 — двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина полки 81 мм; площадь сечения А2 = 20, 2 см2;
3 — лист 5x100; толщина 5 мм; ширина 100 мм; площадь сечения Аз = 0, 5 • 10 = 5 см2.
2. Координаты центров тяжести каждой фигуры можно определить по чертежу.
Составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата Xс = 0.

Тема 1. 6. Центр тяжести 65
Контрольные вопросы и задания
1. Почему силы притяжения к Земле, действующие на точки тела, можно принять за систему параллельных сил?
2. Запишите формулы для определения положения центра тяжести неоднородных и однородных тел, формулы для определения положения центра тяжести плоских сечений.
|
|
|
3. Повторите формулы для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга.
4. Что называют статическим моментом площади?
5. Вычислите статический момент данной фигуры относительно оси Ox. h = 30 см; b = 120 см; с = 10 см (рис. 8. 6).

6. Определите координаты центра тяжести заштрихованной фигуры (рис. 8. 7). Размеры даны в мм.
7. Определите координату у фигуры 1 составного сечения
(рис. 8. 8).
При решении воспользоваться справочными данными таблиц ГОСТ «Сталь горячекатанная» (см. Приложение 1).

66 Лекция 9
ЛЕКЦИЯ 9
Тема 1. 7. Основные понятия кинематики.
Кинематика точки
Иметь представление о пространстве, времени, траектории, пути, скорости и ускорении.
Знать способы задания движения точки [естественный и координатный).
Знать обозначения, единицы измерения, взаимосвязь кинематических параметров движения, формулы для определения скоростей и ускорений (без вывода).
Кинематика рассматривает движение как перемещение в пространстве. Причины, вызывающие движение, не рассматриваются. Кинематика устанавливает способы задания движения и определяет методы определения кинематических параметров движения.
Основные кинематические параметры
Траектория
Линию, которую очерчивает материальная точка при движении в пространстве, называют траекторией.
Траектория может быть прямой и кривой, плоской и пространственной линией.
Уравнение траектории при плоском движении: у = f(x).
Пройденный путь
Путь измеряется вдоль траектории в направлении движения. Обозначение — S, единицы измерения — метры.
|
|
|
Уравнение движения точки
Уравнение, определяющее положение движущейся точки в зависимости от времени, называется уравнением движения.
Положение точки в каждый момент времени можно определить по расстоянию, пройденному вдоль траектории от некоторой неподвижной точки, рассмат-

 Тема 1. 7. Основные понятия кинематики 67
Тема 1. 7. Основные понятия кинематики 67
риваемой как начало отсчета (рис. 9. 1). Такой способ задания движения называется естественным.
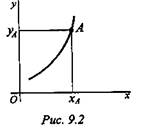
Таким образом, уравнение движения можно представить в виде S = f(t). Положение точки можно также определить, если известны ее координаты в зависимости от времени (рис. 9. 2). Тогда в случае движения на плоскости должны быть заданы два уравнения: 
В случае пространственного движения добавляется и третья координата z= f3(t).
Такой способ задания движения называют координатным.
|
|
|


