 |
Скорость движения. Ускорение точки. Примеры решения задач. Решение. Если точка за равные промежутки времени проходит равные расстояния, то движение называют равномерным
|
|
|
|
Скорость движения
Векторная величина, характеризующая в данный момент быстроту и направление движения по траектории, называется скоростью.
Скорость — вектор, в любой момент направленный по касательной к траектории в сторону направления движения (рис. 9. 3).

Если точка за равные промежутки времени проходит равные расстояния, то движение называют равномерным. Средняя скорость на пути AS определяется как 
где AS — пройденный путь за время Д*; At — промежуток времени.
Если точка за равные промежутки времени проходит неравные пути, то движение называют неравномерным.
В этом случае скорость — величина переменная и зависит от времени v = f(t).
При рассмотрении малых промежутков времени (∆ t —► 0) средняя скорость становится равной истинной скорости движения в данный момент. Поэтому скорость в данный момент определяют как
68 Лекция 9
производную пути по времени:
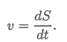
За единицу скорости принимают 1 м/с. Иногда скорость измеряют в км/ч,
1000
1 км/ч = ------ = 0, 278 м/с.
3600
Ускорение точки
Векторная величина, характеризующая быстроту изменения скорости по величине и направлению, называется ускорением точки.
Скорость точки при перемещении из точки М1 в точку M2 меняется по величине и направлению. Среднее значение ускорения за этот промежуток

При рассмотрении бесконечно малого промежутка времени среднее ускорение превратится в ускорение в данный момент:
|
|
|
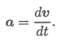

Обычно для удобства рассматривают две взаимно перпендикулярные составляющие ускорения: нормальное и касательное (рис. 9. 5).
Нормальное ускорение ап характеризует изменение скорости по направлению и определяется как
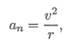
где г — радиус кривизны траектории в данный момент времени.
Нормальное ускорение всегда направлено перпендикулярно скорости к центру дуги.
Касательное ускорение аt характеризует изменение скорости по величине и всегда направлено по касательной к траектории; при ускорении его направление совпадает с направлением скорости, а
Тема 1. 7. Основные понятия кинематики 69
при замедлении оно направлено противоположно направлению вектора скорости.
Формула для определения касательного ускорения имеет вид:

Значение полного ускорения определяется как
 (рис. 9. 6).
(рис. 9. 6).

Примеры решения задач
Пример 1. Дано уравнение движения точки: S = 0, 36t2 + 0, 18t. Определить скорость точки в конце третьей секунды движения и среднюю скорость за первые 3 секунды.
Решение

Пример 2.
Точка движется по кривой радиуса r = 10 м согласно уравнению S = 2, 5t2 + 1, 2t + 2, 5 (рис. 9. 6).
70 Лекция 9
Определить полное ускорение точки в конце второй секунды движения и указать направление касательной и нормальной составляющих ускорения в точке М.
Решение
|
|
|
d v
1. Касательное ускорение определяется как at = —.
dS dt
Уравнение скорости: v = ----.
dt
Скорость будет равна v = 2 • 2, 5t + 1, 2; v = 5t + 1, 2 (м/с).
Касательное ускорение: at = v' = 5 м/с² .
Вывод: касательное ускорение не зависит от времени, оно постоянно.
v²
2. Нормальное ускорение: ап = —.
r
Скорость на второй секунде будет равна v2 = 5 ∙ 2+1, 2 = 11, 2 м/с.
(11, 2)²
Величина нормального ускорения: аn2 = ——— = 12, 54 м/с² .
10
3. Полное ускорение: а = √ at² + an² .
Полное ускорение в конце второй секунды:
а2 = √ 52 + 12, 542 = 13, 5 м/с2.
4. Нормальное ускорение направлено перпендикулярно скорости к центру дуги.
Касательное ускорение направлено по касательной к кривой и совпадает с направлением скорости, т. к. касательное ускорение — положительная величина (скорость растет).
|
|
|


