 |
Тема 1.10. Сложное движение точки.
|
|
|
|
Тема 1. 10. Сложное движение точки.
Сложное движение твердого тела
Иметь представление о системах координат, об абсолютном, относительном и переносном движениях.
Знать разложение сложного движения на относительное и переносное, теорему сложения скоростей.
Знать разложение плоскопараллельного движения на поступательное и вращательное, способы определения мгновенного центра скоростей.
Основные определения
Сложным движением считают движение, которое можно разложить на несколько простых. Простыми движениями считают поступательное и вращательное.
Для рассмотрения сложного движения точки выбирают две системы отсчета: подвижную и неподвижную.
Движение точки (тела) относительно неподвижной системы отсчета называют сложным, или абсолютным.
Подвижную систему отсчета обычно связывают с движущимся телом. Движение подвижной системы отсчета относительно неподвижной называют переносным.
Движение материальной точки (тела) по отношению к подвижной системе называют относительным.
Примером может служить движение человека по эскалатору метро. Движение эскалатора — переносное движение, движение человека вниз или вверх по эскалатору — относительное, а движение по отношению к неподвижным стенам станции — сложное (абсолютное) движение.
При решении задач используют теорему о сложении скоростей:
При сложном движении точки абсолютная скорость в каждый момент времени равна геометрической сумме переносной (ve) и относительной (vr) скоростей:
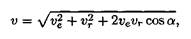а — угол между векторами vе и vr
Тема 1. 10. Сложное движение точки 87
|
|
|
Плоскопараллельное движение твердого тела
Плоскопараллельным, или плоским, называется такое движение твердого тела, при котором все точки тела перемещаются параллельно некоторой неподвижной в рассматриваемой системе отсчета плоскости.
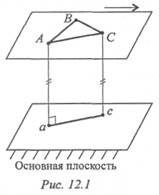
Плоскопараллельное движение можно изучать, рассматривая любое плоское сечение тела, параллельное неподвижной плоскости, называемой основной (рис. 12. 1).
Все точки тела, расположенные на прямой, перпендикулярной к основной плоскости, движутся одинаково.
Плоскопараллельное движение изучается двумя методами: методом разложения сложного движения на поступательное и вращательное и методом мгновенных центров скоростей.
Метод разложения сложного движения на поступательное и вращательное
Плоскопараллельное движение раскладывают на два движения: поступательное вместе с некоторым полюсом и вращательное относительно этого полюса.
Разложение используют для определения скорости любой точки тела, применяя теорему о сложении скоростей (рис. 12. 2).
Точка А движется вместе с точкой В, а затем поворачивается
88 Лекция 12
вокруг В с угловой скоростью ш, тогда абсолютная скорость точки А будет равна
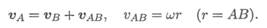
Примером плоскопараллельного движения может быть движение колеса на прямолинейном участке дороги (рис. 12. 3).
Скорость точки М vМ = ve + vr,
ve — скорость центра колеса переносная;
vr — скорость вокруг центра относительная.
уОх — неподвижная система координат,
у101Х1 — подвижная система координат, связанная с осью колеса.
Метод определения мгновенного центра скоростей
|
|
|
Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложное движение представляют в виде цепи вращений вокруг разных центров.
Задача сводится к определению положения мгновенного центра вращений (скоростей) (рис. 12. 4).
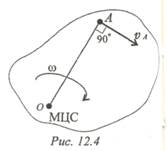
Мгновенным центром скоростей (МЦС) является точка на плоскости, абсолютная скорость которой в данный момент равна нулю.
Вокруг этой точки тело совершает поворот со скоростью ω.
Скорость точки А в данный момент равна va = ω OA,
т. к. va — линейная скорость точки А, вращающейся вокруг МЦС.
Существуют три способа определения положения мгновенного центра скоростей.
Первый способ. Известна скорость одной точки тела va и угловая скорость вращения тела ω (рис. 12. 5).
Точку О находим на перпендикуляре к вектору скорости va.
Тема 1. 10. Сложное движение точки 89
Второй способ. Известны скорости двух точек тела va и vB они не параллельны (рис. 12. 6).
Проводим из точек А и В два перпендикуляра к известным векторам скоростей.
На пересечении перпендикуляров находим МЦС. Далее можно найти скорость любой точки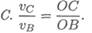 
Третий способ. Известны скорости двух точек тела, и они параллельны (va║ vB) (рис. 12. 7).
Соединяем концы векторов, МЦС находится на пересечении линии, соединяющей концы векторов с линией АВ ( рис. 12. 7 ). При поступательном движении тела (рис. 12. 7в) МЦС отсутствует.
90 Лекция 12
|
|
|
