 |
Основные задачи регрессионного анализа.
|
|
|
|
РЕГРЕССИОННЫЙ АНАЛИЗ
Санкт-Петербург
УДК 621.301
ББК 32.88
Д14
Рецензенты:
Кандидат технических наук, доцент СПбГПУ В.Е. Евдокимов
Кандидат технических наук, начальник отдела реализации проектов
ООО «БСС» А.А. Зотов
Попов С.С. Регрессионный анализ: текст лекций /С.С. Попов– 2012. – 142 с.
В тексте лекций последовательно изложены теоретические основы построения линейных моделей статических объектов. Особое внимание уделено вопросам построения устойчивых к выбросам моделей данных.
Текст лекций ориентирован на студентов высших учебных заведений, проходящих подготовку на степень магистра по направлениям: «Информатика и вычислительная техника», «Программная инженерия», «Системный анализ и управление».
Попов С.С., 2011
© Санкт-Петербургский государственный
политехнический университет, 2011
ОГЛАВЛЕНИЕ
Введение................................................................................................... 4
1. Основные задачи регрессионного анализа........................... 5
1.1 Аппроксимация таблиц наблюдений непрерывными параметрическими функциями........................... 9
1.2 Нелинейные модели, приводимые к линейным относительно параметров............................................................................................................................................. 16
1.3 МНК оценивание коэффициентов связанных линейных.............................................................................. 16
уравнений........................................................................................................................................................................... 16
2. Статистические свойства МНК оценок................................. 22
2.1 Теорема Маркова.................................................................................................................................................... 27
2.2 Оценивание дисперсии ошибок наблюдений................................................................................................. 30
|
|
|
2.3 Обобщенный метод наименьших квадратов.................................................................................................... 32
2.3.1 Взвешенный метод наименьших квадратов.............................................................................................. 34
3. МНК-оценивание при наличии линейных ограничений..... 35
3.1 Проверка гипотез о значениях линейных функций....................................................................................... 37
параметров линейной модели...................................................................................................................................... 37
3.2 Приложения критерия Фишера........................................................................................................................ 40
3.2.1 Задача о сравнении средних двух независимых нормальных выборок.......................................... 40
3.2.2 Задача взвешивания....................................................................................................................................... 42
3.2.3 Линейная одномерная регрессия................................................................................................................. 47
3.2.4 Множественная регрессия............................................................................................................................ 51
3.2.5 Каноническая форма модели........................................................................................................................ 54
3.3 Критерий Стьюдента............................................................................................................................................... 58
3.4 Построение доверительных интервалов для линейных комбинаций параметров и значений регрессии. 60
3.5 Процедуры MatLab подбора регрессий............................................................................................................ 63
4. Выбор матрицы плана при планировании экспериментов. 66
4.1 Ортогональная структура матрицы плана........................................................................................................ 71
4.2 Понятие оптимального плана............................................................................................................................... 73
5. Полиномиальная регрессия........................................................ 76
5.1 Процедура Форсайта получения ортогональных полиномов................................................................. 78
5.2 Построение ортогональных полиномов на системе........................................................................................ 79
|
|
|
равноотстоящих точек................................................................................................................................................... 79
5.3 Регрессия на ортогональных полиномах........................................................................................................... 80
5.4 Оптимальное расположение точек при полиномиальной............................................................................. 81
регрессии............................................................................................................................................................................ 81
5.4.1 Задача интерполяции....................................................................................................................................... 82
5.4.2 Задача оценки параметров полинома..................................................................................................... 83
5.4.3 Задача экстраполяции..................................................................................................................................... 84
5.5 Кусочно-полиномиальная аппроксимация....................................................................................................... 85
5.6 Многомерная полиномиальная регрессия......................................................................................................... 88
5.7 Выбор порядка полиномиальной модели......................................................................................................... 89
6. Подбор регрессионной модели при плохо обусловленной информационной матрице................................................................ 89
6.1 Смещенное оценивание.......................................................................................................................................... 96
6.2 Удаление переменной............................................................................................................................................ 101
6.3 Ортогональное разложение матрицы плана.............................................................................................. 102
при решении задач МНК............................................................................................................................................. 102
6.4 Применение сингулярного разложения в задаче построения линейной регрессии.......................... 105
7. Робастное оценивание............................................................... 110
7.1 Устойчивые методы оценивания параметров регрессионной модели................................................... 117
7.2 Точки разбалансировки...................................................................................................................................... 120
7.3 Итерационный взвешенный метод наименьших квадратов (ИВМНК)................................................. 125
8. Следствия нарушения основных предположений МНК.. 129
8.1 Неполнота моделей.............................................................................................................................................. 130
|
|
|
8.2 Ошибки, связанные с избыточностью модели.............................................................................................. 132
7.6 Неверные предположения о дисперсионной матрице ошибок................................................................. 134
8.4 Смещение оценок, вызванное ошибками задания регрессоров................................................................ 135
8.5 Диагностика регрессионной модели............................................................................................................... 136
БИБЛИОГРАФИЧЕСКИЙ СПИСОК......................................................................................................................... 141
Введение.
Регрессионный Анализ с одной стороны является примером практической реализации результатов “Конструктивной теории функций”, а с другой – разделом “Прикладной статистики”. Основной задачей регрессионного анализа, является подбор функционального описания таблиц наблюдений и применение этого приближения для нахождения возможных значений таблицы в точках, отличных от изначально имеющихся в таблице наблюдений (задача построения прогноза значений таблицы наблюдений, задача интерполяции и экстраполяции).
Подбор функционального описания таблиц наблюдений реализуется процедурами построения “множественной регрессии”. Практически в любом пакете компьютерных программ, ориентированных на выполнение научных или статистических расчетов (STATISTICA, StatGraphics, MatLab и др.), имеются процедуры оценки параметров множественной регрессии.
В учебном пособии рассматриваются некоторые аспекты вычислительных и статистических особенностей процедур построения “множественной регрессии”.
Основные задачи регрессионного анализа.
Научные эксперименты, обычно сопровождаются попыткой формализации возможных закономерностей или связей между отдельными явлениями или событиями, относящимися к объекту наблюдения. Обнаружив факт наличия связи между переменными, назовем их - 
, характеризующими объект, исследователь продолжает целенаправленно изучать объект. При этом выбирается переменная, представляющая наибольший интерес, и уточняется ее зависимость от остальных. Пусть мы исследуем зависимость переменной 
от 
. Данные для построения этой зависимости получают, выполняя эксперименты, в которых переменные устанавливаются на фиксированных уровнях, и регистрируется статический отклик объекта на такое возмущение. Результаты 
экспериментов записываются в таблицу:
|
|
|
. 1.1
Таблица наблюдений (1.1) - уже оформленный отчет о найденных связях значений переменной со значениями остальных, но обычно желают получить более емкий и компактный ответ в виде функциональной связи 
. 1.2
Зависимость (1.2) должна быть дополнена указаниями о том, на каких множествах значений переменных 
справедлива (1.2). Чаще других рассматривается случай непрерывного изменения независимых переменных в интервалах:
, 
, 
, 
1.3
Независимые переменные в задачах построения (1.2) называют регрессорами, факторами, предикторами.
Задача построения зависимостей (1.2) по таблицам наблюдений (1.1) составляет содержание регрессионного анализа.
Главная задача, которая решается с помощью регрессионного анализа - создание математических моделей статических объектов или явлений на основе результатов экспериментов или наблюдений. Эти модели представляют собой определенные математические соотношения между показателями работы объекта, выходными характеристиками или откликами объекта и входными переменными, регрессорами, факторами. Любая модель отражает только некоторые характерные черты объекта и никогда не бывает его точным описанием. Для одного и того же объекта можно создать множество моделей, причем каждая описывает лишь один из показателей, интересующих исследователя.
Например, в качестве выходных характеристик эмалевых красок могут рассматриваться различные свойства пленки, образующейся после нанесения краски: блеск, твердость, ударная прочность и др.
А в качестве независимых переменных будут выступать компоненты, составляющие краску:
35-процентный раствор алкидной смолы в олифе (
),
40-процентный алкидной смолы в олифе (
),
карбоминформальдегидный лак (
),
меламинформальдегидный лак (
),
двуокись титана (
),
цинковые белила(
),
ксилол(
),
а также некоторые факторы, определяющие процесс покрытия изделия эмалевой краской:
время обжига (
),
температура обжига (
) и др.
В зависимости от целей исследования один и тот же объект с одинаковыми показателями может описываться различными моделями. Так, если цель - изучение механизма химической реакции, лучше всего подходит аналитико-экспериментальные модели, составляемые на основе физических и химических закономерностей, которым подчиняется объект.
|
|
|
Когда же нужно определить оптимальный технологический режим, часто достаточно воспользоваться моделью, описывающей выходные характеристики как полиноминальные функции факторов.
Если по наблюдениям (1.1) строят линейную функцию (1.2) регрессоров, говорят о задаче построения линейной регрессии:
1.4
Часто одни регрессоры бывают функциями других. Например, в задаче подбора зависимости:
1.5
есть функция одной переменной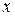 
; с другой стороны (1.5) это линейная комбинация 
регрессоров 
, 
; регрессоры - различные, выбираемые исследователем, взаимно независимые функции переменной .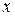
Как построить функцию (1.2) на основе таблицы наблюдений (1.1)?
Обсуждать поставленные проблемы имеет смысл только после того, как выбран тип (вид) функции в (1.2). Обычно выбирают параметрические зависимости (1.2). Это позволяет использовать процедуры параметрической оптимизации при подгонке наилучшей в смысле некого критерия 
функции (1.2) к таблице (1.1). Такими параметрическими функциями в частности являются линейные регрессии (1.4,1.5).
Пример 1. Исследование влияния медикаментов на подопытного кролика
На этом примере демонстрируются основные положения подбора функции для описания таблицы наблюдений. В эксперименте по изучению влияния некого препарата на содержание азота в крови обе переменные, характеризующие состояние объекта наблюдения, непрерывны.
Независимая переменная – доза препарата легко контролируется и задается с высокой точностью, тогда как зависимая – содержание азота в крови - подвержена сильным искажениям. Исход экспериментов - результаты анализа крови - определяется не только количеством вводимого препарата, но и многими другими причинами и явлениями, сопутствующими опытам.
Анализ результатов шести наблюдений, представленных на рисунке крестиками, позволяет установить общую тенденцию убывания азота с увеличением дозы препарата. Выберем для математического описания замеченной закономерности одну из самых простых зависимостей – линейную: 
. Чтобы построить прямую, достаточно двух точек. Однако, выбирая различные пары можно построить совершенно разные прямые. Например, прямая 1 проходит через две точки из шести, но сильно отклоняется от остальных прямых, проходящих через другие пары точек и не отражает общую тенденцию изменения от 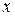. Можно попытаться провести кривую, проходящую через все точки таблицы – интерполяционный полином, но это также не лучшее решение. Такой полином в точности проходит через все точки таблицы, но между любой парой соседних точек может сильно отличаться по величине от значений в ближайших узлах.
Таблицу наблюдений можно аппроксимировать кривой (1.2). Т.е. представить таблицу функцией, которая может быть и не пройдет ни через один из узлов таблицы, но в смысле некого критерия менее других отклоняется от наблюдений таблицы. На рисунке такой функцией является прямая 2, аппроксимирующая таблицу, которая лучше других отражает общую тенденцию убывания азота в крови с увеличением дозы вводимого препарата. Есть еще одно обстоятельство в пользу аппроксимации таблиц. Обычно зависимая переменная в значительной степени искажена помехами. В таком случае может и не следует стремиться проводить кривую через узлы таблицы?
|
|
|
