Аппроксимация таблиц наблюдений непрерывными параметрическими функциями.

 

Далее мы рассмотрим проблемы, связанные с аппроксимацией таблиц наблюдений, и, если не оговорено другое, будем считать что:

- все переменные, значения которых приведены в таблице, непрерывны,

- зависимость , предлагаемая для описания таблицы, есть линейная комбина­ция независимых переменных (регрессоров, факторов, предикторов) т.е. функциональная зависимость вида (1.4, 1.5).

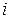Обозначим -ый регрессор в списке из регрессоров таблицы наблюдений (1.1), а - его значение в -ом эксперименте. Таблицу значений всех регрессоров в экспериментах можно записать как матрицу размера ; наблюдения откликов 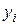в тех же экспериментах представить вектором с элементами :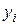

, ,

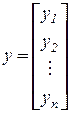- матрица плана, - вектор наблюдений, - вектор параметров линейных функций (1.4, 1.5).

В этих обозначениях вектор значений линейной функции вида (1.4, 1.5), подбираемой по некоторым правилам к таблице наблюдений:

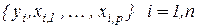; есть: 1.6

; 1.7

или ,

где 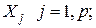векторы (n x 1) значений p регрессоров в экспериментах (столбцы матрицы плана ).

Говорят, что:

- (1.7) реализует линейную модель связи переменной с регрессорами ,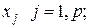

- (1.7) – линейная аппроксимация связи ;

- (1.7) – линейная модель данных (1.6)).

Здесь уместно указать критерии, на основе которых производится подбор наилучшей аппроксимирующей функции (1.7). При подборе функции (1.7) варьируются параметры модели и выбирается то значение вектора , при котором обеспечивается наименьшее отклонение вектора приближения от вектора наблюдений .

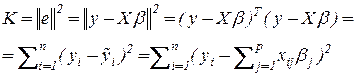Введем вектор ошибки аппроксимации , как разность вектора наблюдений и аппроксимирующей функции, при одних и тех же значениях регрессоров. Очевидно, лучшей является та аппроксимация (тот набор параметров ), для которой эта разность мала. Мерой сте­пени отклонений могут быть, например,: , 1.8

где - евклидова норма вектора , либо:

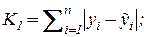или

Аппроксимация таблицы наблюдений (т.е. выбор значения параметров ) тем лучше, чем ближе в соответствии с выбранной мерой векторы и . Мера используется в критериях среднеквадратической близости, мера - абсолютной близости, мера - равномерной близости.

В задачах подбора аппроксимирующей кривой по таблице наблюдений чаще других используют критерий на основе меры (1.8):

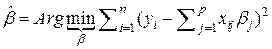
Процедура выбора значений вектора параметров зависимости (1.7), минимизацией суммы квадратов отклонений значений аппроксимирующей кривой от наблюдений (1.8), носит название “метода наименьших квадратов ”.

Критерий близости есть функция вектора параметров . Выберем так, чтобы критерий принимал минимальное значение, т.е. выберем так, чтобы обеспечить наилучшее в смысле малости критерия приближение таблицы наблюдений функцией (1.7).

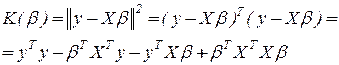
и учитывая, что , получаем:

Минимум критерия достигается при тех значениях , для которых .

Вычислим .

Производные скалярного произведения и квадратичной формы по вектору равны соответственно: 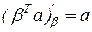; ; от не зависит и ее производная .

Отсюда: 1.9

Итак , доставляющее критерию минимальное значение, есть решение уравнения (1.9), которое называют нормальным уравнением.

Матрица размера всегда симметрична и носит название нормальной матрицы.

Если матрица Х размера 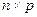() имеет ранг р ( 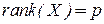), ее называют матрицей полного ранга.

Если 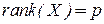, то не вырождена и имеет обратную 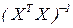. Решение уравнения (1.9) в этом случае единственно и равно:

. 1.10

Значение критерия в точке минимума носит название остаточной суммы квадратов отклонений; обозначается - 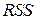и равно:

= ; 1.11

Здесь: в силу (1.9).

 

Если в (1.11) подставить (1.10). получим:

1.12

Матрица в (1.12) носит название матрицы подгонки или матрицы проектирования.

Итак, если связь переменной с регрессорами 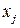линейна - (1.7),

если ,

если критерием близости аппроксимирующей кривой и таблицы наблюдений является (1.8),

то единственный вектор , доставляющий минимум критерию , находят решением нормального уравнения (1.9), либо вычислением матричного выражения (1.10).

Вектор - МНК-оценка параметров регрессионной модели (1.7).

Не следует думать, что линейная модель (1.7) сильно ограничивает исследователя в выборе формы связи переменной с регрессорами. Если учесть возможность введения в модель дополнительных регрессоров, которые являются функциями основных, то возможности метода наименьших квадратов - МНК существенно расширяются. При этом надо следить за тем, чтобы столбцы матрицы плана были линейно независимы.

Пример 2. Приблизить данные таблицы наблюдений кубической параболой.

Зададим модель связи (регрессию на 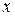). Здесь помимо основного регрессора 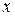в модель включены дополнительно регрессоры-функции 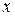: 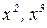и регрессор равный 1 ().

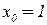Матрица плана размера этой задачи есть

, вектор параметров ;

если матрица имеет ранг равный 4, т.е. столбцы или строки образуют систему линейно независимых векторов на множестве значений , то наилучшая в смысле критерия (1.8) кубическая парабола имеет коэффициенты 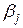, являющиеся элементами вектора .

Пример 3. Подобрать, используя приведенные выше процедуры аппроксимации, зависимость вида по таблице наблюдений . К сожалению, сделать это, используя оценки (1.9, 1.10), невозможно, поскольку предлагаемая зависимость не линейна (условие 1.7 не выполняется) относительно па­раметров .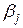

 

Импорт, потребление, производство и изменение запасов во Франции с 1949 по 1966 г.г.

Таблица взята из книги (Маленво, Эконометрия)

 

N п/п	Годы 19_ _	Импорт	Валовой продукт-	Изменение запасов -	Производство
		15.9	149.3	4.2	103.1
		16.4	161.2	4.1	114.8
		19.0	171.5	2.11	123.2
		19.1	175.5	2.11	126.9
		18.8	180.8	1.1	132.1
		20.4	190.7	2.2	137.7
		22.7	202.1	2.1	146.0
		26.5	212.4	5.6	154.1
		23.1	226.1	5.0	162.3
		27.6	231.0	5.1	164.3
		26.3	239.0	0.7	167.6
		31.1	258.0	5.6	176.8
		33.3	269.8	2.19	186.6
		37.0	288.4	2.11	199.7
		43.3	304.5	4.6	212.19
		49.0	322.14	7.0	222.18
		50.3	336.8	1.2	232.0
		56.6	352.19	4.5	242.9

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: