 |
Подбор регрессионной модели при плохо обусловленной информационной матрице.
|
|
|
|
В силу различных причин (то ли неудачно выбраны регрессоры, то ли неудачно выставлены их значения) при решении задачи МНК  столбцы матрицы плана
столбцы матрицы плана  размера
размера  и ранга
и ранга  как векторы в n - мерном пространстве могут оказаться почти линейно зависимыми.
как векторы в n - мерном пространстве могут оказаться почти линейно зависимыми.
Пример 1. Размеры сердца и грудной клетки.
Биостатистик провел серию измерений объема грудной клетки группы 12 – летних мальчиков с интервалом в 6 месяцев; одновременно проводились исследования объемов их сердец на основе рентгенограмм, число обследуемых мальчиков – 114. На основе этих измерений было построено регрессионное уравнение:  , где
, где 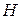 - объем сердца,
- объем сердца,  - первый замер объема грудной клетки,
- первый замер объема грудной клетки,  - второй замер объема грудной клетки спустя 6 месяцев. Затем была проведена еще одна серия подобных измерений на другой группе мальчиков того же возраста. На этот раз уравнение регрессии оказалось
- второй замер объема грудной клетки спустя 6 месяцев. Затем была проведена еще одна серия подобных измерений на другой группе мальчиков того же возраста. На этот раз уравнение регрессии оказалось  . Такая значительная разница в коэффициентах уравнений регрессии конечно смущает. Какому из уравнений верить?
. Такая значительная разница в коэффициентах уравнений регрессии конечно смущает. Какому из уравнений верить?
В данном случае произошло следующее. Для каждого мальчика замеры  и
и  отличались очень мало. Причем различия объяснялись в основном не естественным ростом, а ошибками измерений.
отличались очень мало. Причем различия объяснялись в основном не естественным ростом, а ошибками измерений.
Можно было бы использовать одно усредненное значение объема грудной клетки  , что привело бы к уравнению
, что привело бы к уравнению  . Коэффициент 11 есть сумма параметров при регрессорах
. Коэффициент 11 есть сумма параметров при регрессорах  и
и  в обоих уравнениях. С геометрической точки зрения экспериментальные точки лежат в трехмерном пространстве (
в обоих уравнениях. С геометрической точки зрения экспериментальные точки лежат в трехмерном пространстве ( ) практически на одной прямой; плоскость, построенная по этим точкам становится неустойчивой, небольшие изменения положения точек приводит к значительным изменениям коэффициентов регрессии. Про такие задачи говорят, что они плохо определены.
) практически на одной прямой; плоскость, построенная по этим точкам становится неустойчивой, небольшие изменения положения точек приводит к значительным изменениям коэффициентов регрессии. Про такие задачи говорят, что они плохо определены.
|
|
|
Несмотря на значительное различие в коэффициентах регрессий  и
и  обе модели предсказывают размеры сердца практически одинаково. Геометрически это можно объяснить тем, что все точки (
обе модели предсказывают размеры сердца практически одинаково. Геометрически это можно объяснить тем, что все точки ( ) лежат почти на прямой
) лежат почти на прямой  в плоскости
в плоскости  и увеличение одного из регрессионных коэффициентов за счет другого не приводит к заметным отклонениям зависимой переменной. В этой задаче сумма регрессионных коэффициентов при регрессорах
и увеличение одного из регрессионных коэффициентов за счет другого не приводит к заметным отклонениям зависимой переменной. В этой задаче сумма регрессионных коэффициентов при регрессорах  и
и  в каждой из регрессий оказалась устойчивой и модель
в каждой из регрессий оказалась устойчивой и модель  хорошо предсказывает зависимую переменную.
хорошо предсказывает зависимую переменную.
Наличие почти линейно зависимых регрессоров привела к неустойчивости коэффициентов регрессии и необходимости пересмотра модели данных.
Опираться на коэффициенты регрессии в выводах о характере связей отклика с регрессорами следует с осторожностью.
Пример 2. Точность поражения целей при бомбовых ударах союзной авиации в Европе. При исследовании эффективности бомбометания было составлено уравнение регрессии, в которое были включены такие факторы, как высота бомбометания, тип самолета, скорость звена бомбардировщиков, размер звена, число истребителей противника и ряда других. Можно ожидать, что точность попадания обратно пропорциональна высоте и скорости звена бомбардировщиков и что для разных типов самолета результаты будут разными. Но удивительным оказалось то, что в соответствии с уравнением регрессии точность попадания повышалась с ростом числа истребителей противника. Этот феномен объяснился тем, что в уравнение регрессии не была включена переменная, описывающая облачность. А при сильной облачности над целью истребители противника обычно не появлялись, зато и ошибки бомбометания были велики. Это так называемое явление заместителя; регрессор “число истребителей противника” подменяет сильно связанный с ним регрессор ”облачность”. Если среди регрессоров, включенных в модель, оказывается несколько казалось бы не связанных между собой регрессоров, но зависящих от одного и того же заместителя эффект сильной связи между столбцами снова дает о себе знать.
|
|
|
Система векторов в n- мерном пространстве  линейно зависима, если найдутся такие, не все равные нулю, числа
линейно зависима, если найдутся такие, не все равные нулю, числа  , что
, что  . 6.1
. 6.1
Если равенство (6.1) выполняется лишь приближенно:  6.2
6.2
столбцы матрицы  - векторы
- векторы  - почти линейно зависимы. При этом говорят о плохой обусловленности матрицы
- почти линейно зависимы. При этом говорят о плохой обусловленности матрицы  . При плохой обусловленности матрица
. При плохой обусловленности матрица  близка к вырожденной, ее обращение сопровождается большими вычислительными ошибками. Условие (6.2) не строгое и можно говорить, что все матрицы в той или иной мере плохо обусловлены. Мерой обусловленности квадратной матрицы
близка к вырожденной, ее обращение сопровождается большими вычислительными ошибками. Условие (6.2) не строгое и можно говорить, что все матрицы в той или иной мере плохо обусловлены. Мерой обусловленности квадратной матрицы  является число обусловленности
является число обусловленности  ,
,
где  - собственные числа матрицы
- собственные числа матрицы  .
.
Говорят, что матрица  плохо обусловлена, если
плохо обусловлена, если  .
.
Применение ортогонального разложения матрицы для выявления степени связи ее столбцов и числа обусловленности матрицы  .
.
По определению квадратная матрица  ортогональна, если
ортогональна, если  .
.
1. Ортогональная матрица сохраняет евклидову норму векторов при преобразованиях:
если  , то
, то 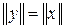 ,
,  -знак нормы вектора. 6.3
-знак нормы вектора. 6.3
2. Для любой матрицы  существует представление
существует представление  , где
, где 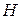 и
и  ортогональные матрицы размера
ортогональные матрицы размера  и
и 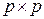 соответственно, а матрица
соответственно, а матрица  размера
размера  .
.
Пусть для матрицы  размерностью
размерностью  и ранга
и ранга  найдено ортогональное разложение:
найдено ортогональное разложение:  при
при  ;
;
 6.4
6.4
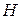 - ортогональная матрица размера
- ортогональная матрица размера  ,
,
 - ортогональная матрица размера
- ортогональная матрица размера 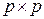 ,
,
 – диагональная матрица размера
– диагональная матрица размера 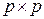 .
.
Диагональные элементы матрицы  называются сингулярными числами, а само разложение (6.4) – сингулярным или SVD-разложением (SVD – singular value decomposition).
называются сингулярными числами, а само разложение (6.4) – сингулярным или SVD-разложением (SVD – singular value decomposition).
Разложение (6.4) проводят так, чтобы сингулярные числа  ,
, 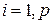 с увеличением номера
с увеличением номера 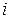 не возрастали (упорядочены по не возрастанию).
не возрастали (упорядочены по не возрастанию).
Сингулярные числа матрицы  ранга
ранга  и собственные значения положительно определенной матрицы
и собственные значения положительно определенной матрицы  связаны соотношением:
связаны соотношением:
 ; 6.5
; 6.5
(собственные значения положительно определенной матрицы
положительны).
В соответствии с (6.5) судить о степени обусловленности матрицы  можно по сингулярным числам, а поскольку они упорядочены по не возрастанию, то:
можно по сингулярным числам, а поскольку они упорядочены по не возрастанию, то:
 . 6.6
. 6.6
Большие значения  соответствуют высокой степени линейной зависимости столбцов матрицы
соответствуют высокой степени линейной зависимости столбцов матрицы  .
.
Пример.

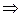

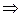
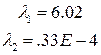
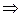
 ;
;
|
|
|
 ;
;  ;
;
Ненулевые недиагональные элементы матрицы  заставляют задуматься о точности вычислений.
заставляют задуматься о точности вычислений.
Сингулярное разложение матрицы 

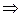
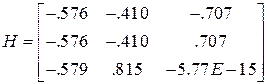


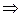
 ,
, 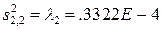 .
.

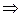

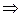
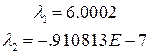
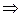
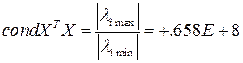
Из-за больших вычислительных ошибок матрица  оказалась даже не положительно определенной и имеет одно отрицательное собственное число; обратная матрица вычислена настолько неверно, что произведение матриц
оказалась даже не положительно определенной и имеет одно отрицательное собственное число; обратная матрица вычислена настолько неверно, что произведение матриц  никак не похоже на единичную матрицу:
никак не похоже на единичную матрицу:
 ;
;  ;
;
Замечания.

Если  , где
, где 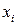 – собственный вектор матрицы
– собственный вектор матрицы  , то
, то  ; т.е. матрица
; т.е. матрица  имеет собственные числа
имеет собственные числа  , а собственные векторы
, а собственные векторы 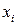 матриц
матриц  и
и  одинаковы.
одинаковы.
Смещенное оценивание.
Рассмотрим линейную модель  ;
;  ;
;  .
.
В соответствии с теоремой Маркова оценка 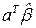 вектора
вектора  имеет минимальную дисперсию в классе всех линейных, несмещенных оценок.
имеет минимальную дисперсию в классе всех линейных, несмещенных оценок.
Если  имеет нормальное распределение, то несмещенная оценка
имеет нормальное распределение, то несмещенная оценка 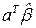 вектора
вектора  имеет минимальную дисперсию в классе всех несмещенных оценок этого вектора.
имеет минимальную дисперсию в классе всех несмещенных оценок этого вектора.
То, что оценка  параметра bj обладает минимальной дисперсией в соответствующем классе оценок, еще никак не гарантирует того, что эта дисперсия будет мала на самом деле.
параметра bj обладает минимальной дисперсией в соответствующем классе оценок, еще никак не гарантирует того, что эта дисперсия будет мала на самом деле.
В частности, если матрица  близка к вырожденной так, что ее наименьшее собственное число, скажем
близка к вырожденной так, что ее наименьшее собственное число, скажем  , близко к нулю, то «полная дисперсия» оценок параметров
, близко к нулю, то «полная дисперсия» оценок параметров  :
:
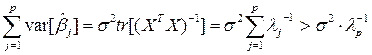
может оказаться слишком большой для практических целей.
Чтобы обойти эту трудность, связанную с «плохой обусловленностью» матрицы  Кеннард ввел класс оценок вида:
Кеннард ввел класс оценок вида:
 ;
;  .
.
известных под названием гребневых оценок (ridge estimator).
Оценка  при
при  смещена.
смещена.

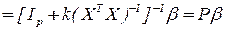
здесь  матрица смещения.
матрица смещения.
Исследование графиков компонент вектора  и соответствующих
и соответствующих  как функции числа
как функции числа  показало:
показало:
1. можно выбрать такие  , что:
, что:
- оценки  становятся устойчивыми, т.е. малые отклонения в данных не приводят к существенным изменениям оценок,
становятся устойчивыми, т.е. малые отклонения в данных не приводят к существенным изменениям оценок,
- остаточная сумма 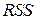 в среднем не слишком велика,
в среднем не слишком велика,
2. Всегда существует такое  , при котором полная среднеквадратическая ошибка оценки
, при котором полная среднеквадратическая ошибка оценки  оказывается меньше полной среднеквадратической ошибки МНК – оценки
оказывается меньше полной среднеквадратической ошибки МНК – оценки  .
.
Действительно, полная среднеквадратическая ошибка оценки  есть:
есть:
|
|
|
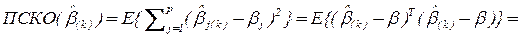
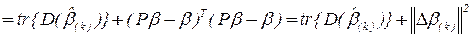
Здесь  - сумма дисперсий всех компонент вектора
- сумма дисперсий всех компонент вектора  .
.
Полная среднеквадратическая ошибка для обычной МНК оценки  :
:
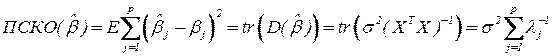
 – собственные числа матрицы
– собственные числа матрицы  .
.
Вычислим  , а сначала саму матрицу
, а сначала саму матрицу  ,
,
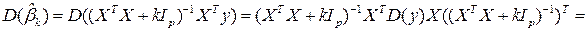
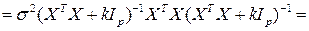
Замечание. Здесь использовать (AB)-1 = B-1 A-1
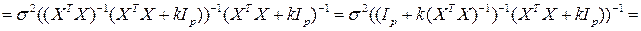
 ;
;
 ,
,
Здесь  собственные числа матрицы
собственные числа матрицы 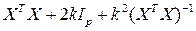
Пусть  - собственные вектора, а
- собственные вектора, а  собственные числа матрицы
собственные числа матрицы  , тогда
, тогда
 ;
;
 ;
; 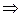
 ;
;
 ;
; 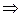
 ;
;
Сложим эти равенства
 .
.
Отсюда следует, что  - есть собственные вектора матрицы
- есть собственные вектора матрицы 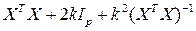 , а
, а
 ;
; 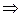

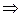
 ее собственные числа.
ее собственные числа.
Итак 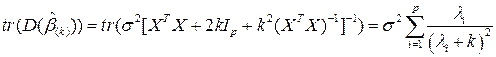
Гребневая оценка МНК - оценка
 ;
;  .
.
 На рисунке кривая 1 изображает
На рисунке кривая 1 изображает  ;
;
кривая 2-  ; 3 -
; 3 -  ; 4 -
; 4 -  .
.
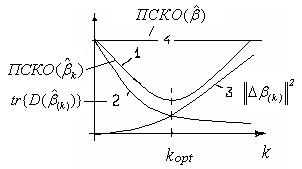
Существует значение  , при котором
, при котором  меньше чем
меньше чем  ; т.е. гребневая оценка оказывается лучше МНК-оценки по критерию малости полной среднеквадратической ошибки.
; т.е. гребневая оценка оказывается лучше МНК-оценки по критерию малости полной среднеквадратической ошибки.
Выбор параметра регуляризации.
Полученная выше, принципиальная возможность построения оценок  , имеющих малую
, имеющих малую  , это еще не решение задачи. Необходимо знать при каких значениях числа k строить оценки
, это еще не решение задачи. Необходимо знать при каких значениях числа k строить оценки  .
.
Графики изменения оценок  ,
,  от параметра регуляризации
от параметра регуляризации  используются для выбора числа
используются для выбора числа  в окончательных расчетах. Начиная с некоторого
в окончательных расчетах. Начиная с некоторого  , вид зависимостей
, вид зависимостей  стабилизируется, что служит основой для выбора
стабилизируется, что служит основой для выбора  .
.
Другой способ выбора числа  :
: 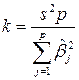 ,
,
где  - обычные МНК оценки, а
- обычные МНК оценки, а  - оценка дисперсии наблюдений
- оценка дисперсии наблюдений  .
.
Варианты критериев качества оценок, используемые в практике подбора линейных регрессионных моделей для таблиц наблюдений
1 Обычный МНК  ;
;
2 Смещенное оценивание  ;
;
где 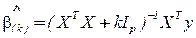
3 Взвешенное смещенное оценивание
 ;
;
Здесь матрица  позволяет задавать различные веса ошибкам
позволяет задавать различные веса ошибкам  и учитывать различную цену потерь от неправильных решений.
и учитывать различную цену потерь от неправильных решений.
Удаление переменной.
Если в задаче  подбора регрессии
подбора регрессии  по таблице наблюдений
по таблице наблюдений 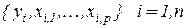
удаляется регрессор, скажем  , то она преобразуется в задачу:
, то она преобразуется в задачу:
 , 6.7
, 6.7
где  - матрица размерности
- матрица размерности  ), образованная (
), образованная ( ) столбцами матрицы
) столбцами матрицы  и вектором
и вектором  , размерности (
, размерности ( ). Матрица
). Матрица  ранга
ранга  положительно определена и имеет собственные числа
положительно определена и имеет собственные числа  . Сингулярные числа матрицы
. Сингулярные числа матрицы  -
-  и собственные числа
и собственные числа  матрицы
матрицы  связаны соотношением
связаны соотношением  . Мерой обусловленности матрицы
. Мерой обусловленности матрицы  является число
является число
 .
.
Известно, что если  , то сингулярные числа матрицы
, то сингулярные числа матрицы  разделяют сингулярные числа матрицы
разделяют сингулярные числа матрицы  , следовательно, и
, следовательно, и  . Поэтому удаление регрессора может улучшить дисперсионные свойства оценок
. Поэтому удаление регрессора может улучшить дисперсионные свойства оценок  по сравнению с
по сравнению с  .
.
Ясно, что  в задаче (6.7) не меньше
в задаче (6.7) не меньше  :
:  .
.
Таким образом, удаление регрессора является средством снижения числа обусловленности матрицы ценой увеличения (неуменьшения) 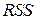 .
.
Трудности метода обычно связаны с перебором регрессоров, подлежащих удалению, и вычислением собственных чисел.
6.3 Ортогональное разложение матрицы плана
При решении задач МНК.
|
|
|
По определению квадратная матрица  ортогональна, если
ортогональна, если  . Ортогональная матрица сохраняет Евклидову норму векторов при преобразованиях:
. Ортогональная матрица сохраняет Евклидову норму векторов при преобразованиях:


Для любой матрицы Х существует представление  , где
, где 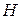 и
и  ортогональные матрицы.
ортогональные матрицы.
При решении задач подбора регрессии методом наименьших квадратов  речь идет о минимизации по b Евклидовой нормы вектора невязок (остатков)
речь идет о минимизации по b Евклидовой нормы вектора невязок (остатков)  ;
;  .
.
Лемма Лоусона - Хенсона.
Пусть в задаче подбора регрессии методом наименьших квадратов  матрица
матрица  размера (
размера ( ) ранга
) ранга  (
( ) представлена в виде:
) представлена в виде:
 ,
,
где 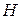 – ортогональная матрица размера (
– ортогональная матрица размера ( ),
),
 – ортогональная матрица размера (
– ортогональная матрица размера ( );
);
 - матрица размера (
- матрица размера ( ), а
), а  матрица размера (
матрица размера ( ) ранга
) ранга  .
.
Определим вектор  :
:
 ;
;  -
-  - мерный вектор,
- мерный вектор,  - (
- ( )-мерный вектор,
)-мерный вектор,
введем новую переменную  :
:
 ;
;  -
-  - мерный вектор,
- мерный вектор,  - (
- ( )-мерный вектор;
)-мерный вектор;
определим  как единственное решение системы:
как единственное решение системы:  .
.
Тогда:
1. Все решения задачи о минимизации  имеют вид:
имеют вид:
 , где
, где  произвольно.
произвольно.
2. Любой вектор  приводит к одному и тому же вектору невязки r:
приводит к одному и тому же вектору невязки r:

3. Для нормы  справедливо:
справедливо:
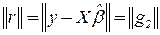
4. Единственным решением минимальной длины является вектор:
 .
.
Доказательство.
1. Заменяя в  ,
,  разложением
разложением  , запишем выражение для квадрата нормы вектора невязки:
, запишем выражение для квадрата нормы вектора невязки:
 для всех
для всех  .
.
Здесь использовано свойство неизменности Евклидовой нормы векторов при ортогональных преобразованиях.
Правая часть имеет минимальное значение при  . 6.8
. 6.8
Уравнение (6.8) имеет единственное решение  , так как ранг
, так как ранг  равен
равен  .
.
Общее решение, доставляющее min  , есть:
, есть:

 , где
, где  произвольно.
произвольно.
Действительно:
 , при любых
, при любых 
 принимает одинаковые значения.
принимает одинаковые значения.
2. Для вектора 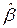 , определяемого уравнением:
, определяемого уравнением:  имеем:
имеем:
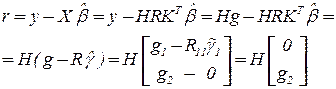
3. Квадрат нормы вектора невязки:
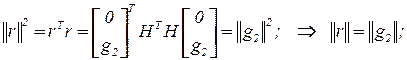
4. Cреди векторов  минимальную длину имеет тот, для которого
минимальную длину имеет тот, для которого  , и так как
, и так как  ,
,
то минимальную длину имеет вектор  . 6.9
. 6.9
Матрица К ортогональна и сохраняет евклидову норму векторов при преобразованиях  и норма
и норма  минимальна для (6.9).
минимальна для (6.9).
Замечание
В случае  вектор
вектор  не содержит составляющих
не содержит составляющих  .
.
Решение минимальной длины единственно и не зависит от конкретного ортогонального разложения (само разложение  не единственно).
не единственно).
В случае, когда  , задача МНК имеет неединственное решение.
, задача МНК имеет неединственное решение.
|
|
|


