 |
Линейная одномерная регрессия.
|
|
|
|
Пусть предполагается линейная связь между наблюдениями 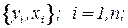 т.е.
т.е.  . При построении линейной одномерной регрессии чаще других проверяется гипотеза о том, что:
. При построении линейной одномерной регрессии чаще других проверяется гипотеза о том, что: 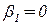 . Это равносильно проверке гипотезы о том, что нет никакой связи между
. Это равносильно проверке гипотезы о том, что нет никакой связи между  , а наблюдаемые изменения у суть проявление случайности.
, а наблюдаемые изменения у суть проявление случайности.
Значим ли коэффициент  в модели
в модели  ?
?
Проверим гипотезу 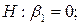 ;
; 
 ,
,  ;
;  ;
;
В решаемой задаче матрица плана есть:
 ,
,  ,
,  ;
; 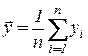 ;
; 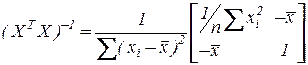
и МНК-оценки параметров  равны:
равны:

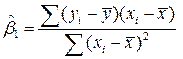 3.10
3.10
 3.11
3.11
Вычисляем 
При  ,
,
 ;
; 


Сравнивая F с критической границей, принимаем решение о степени согласия гипотезы H с наблюдениями.
Запишем еще одно выражение для вычисления F.
Введем выборочный коэффициент корреляции r переменных y и x.
 ; (
; (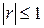 ; из неравенства Коши)
; из неравенства Коши)
Из (3.11)  ;
;  ;
;
из (3.10):
 ; (3.12)
; (3.12)
Вычислим, используя (3.11):  ;
;
Записывая в явном виде квадрат разности величин  , найдем:
, найдем:

отсюда:  ;
;
 ;
; 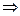
 ;
;
При гипотезе  ; модель данных
; модель данных  ;
;  ; отсюда:
; отсюда: 
Теперь запишем, используя (3.11, 3.12):

Получено еще одно выражение для статистики F. Сравнением его с границей принимаем решение о справедливости гипотезы H. Чем r ближе к единице  , тем больше F и тем с большей вероятностью отклоняется гипотеза H.
, тем больше F и тем с большей вероятностью отклоняется гипотеза H.
Замечание.
1. 
 3.13
3.13
2. Свойство МНК - оценок моделей  , содержащих постоянный регрессор 1 или
, содержащих постоянный регрессор 1 или  ):(
):( - коэффициент при постоянном регрессоре):
- коэффициент при постоянном регрессоре):



 ;
; 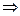
 ; 3.14
; 3.14
- сумма уклонений значений регрессии от наблюдений равна нулю; сумма остатков при МНК аппроксимации таблицы наблюдений равна нулю в моделях, содержащих постоянный регрессор;

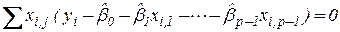 ;
; 
 ;
;
Множественная регрессия.
Множественная регрессия предполагает связь отклика y и многих регрессоров  (больше двух).
(больше двух).
 ;
;  ; 3.15
; 3.15
(здесь число регрессоров равно p;  ).
).
Наибольший интерес представляет гипотеза об отсутствии какой-либо связи отклика и регрессоров:
|
|
|
 ;
;  3.16
3.16
В (3.16) (p-1) ограничений, следовательно, матрица  содержит (p-1) строку и p столбцов.
содержит (p-1) строку и p столбцов.
 ,
, 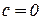 ;
;  .
.
Проверим справедливость гипотезы H (3.16), используя статистику F:

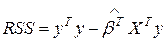 - сумма квадратов отклонений при учете всех коэффициентов модели (3.15)
- сумма квадратов отклонений при учете всех коэффициентов модели (3.15)
 - сумма квадратов отклонений в задаче МНК-оценки параметров модели (3.15.) с учетом ограничений гипотезы H (3.16); модель данных в этом случае
- сумма квадратов отклонений в задаче МНК-оценки параметров модели (3.15.) с учетом ограничений гипотезы H (3.16); модель данных в этом случае  и
и  .
.
Если выполняется условие  , то все регрессоры модели (3.15.), кроме
, то все регрессоры модели (3.15.), кроме  , не оказывают значимого влияния на y.
, не оказывают значимого влияния на y.
Если H отвергается, то остается не ясным какие именно коэффициенты значимы, а какие нет и следует продолжить проверку значимости коэффициентов по отдельности или по группам, используя все ту же статистику F. В качестве одного из рабочих правил Дрейпер и Смит предлагают модифицированный критерий значимости всех коэффициентов модели (3.15), а именно, если выполняется условие  , то все коэффициенты значимы.
, то все коэффициенты значимы.
Полезной мерой степени соответствия аппроксимирующей кривой имеющимся данным является выборочный множественный коэффициент корреляции переменных  ; он определяется как:
; он определяется как:
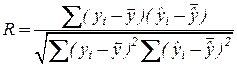 ;
;  ;
;
Величину  называют коэффициентом детерминации и чем больше
называют коэффициентом детерминации и чем больше  , тем лучше построенная аппроксимация соответствует наблюдениям.
, тем лучше построенная аппроксимация соответствует наблюдениям.
Замечание 1. для моделей данных (3.15), содержащих постоянную составляющую ( ):
):
1.  3.17
3.17
из (3.14)  ; и из (3.13)
; и из (3.13)  отсюда следует что смешанное произведение в сумме квадратов равно нулю:
отсюда следует что смешанное произведение в сумме квадратов равно нулю:
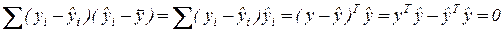 ;
;
2. из (3.14)  ,
, 

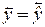 и затем из (3.17):
и затем из (3.17):
 =
= 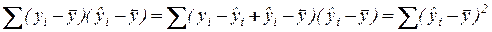 ;
;

 3.18
3.18
Из (3.17,3.18) 
С учетом полученных соотношений статистика F для проверки гипотезы (3.16) есть:
 т.е. чем ближе
т.е. чем ближе  к единице, тем лучше аппроксимация (3.15) соответствует наблюдениям, а гипотеза (3.16) отклоняется с большей вероятностью.
к единице, тем лучше аппроксимация (3.15) соответствует наблюдениям, а гипотеза (3.16) отклоняется с большей вероятностью.
 есть обобщение коэффициента
есть обобщение коэффициента  ; если модель данных
; если модель данных  ,
,
то  .
.
Замечание 2. Критерий проверки произвольной гипотезы вида  , не затрагивающий значения
, не затрагивающий значения  (большинство критериев такие) рассматривают как критерий значимости уменьшения величины
(большинство критериев такие) рассматривают как критерий значимости уменьшения величины  при введении ограничений, до величины
при введении ограничений, до величины 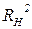 . Всегда
. Всегда  .
.
|
|
|
Пусть 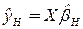 - регрессия, подогнанная к данным с учетом ограничений, не затрагивающих значения параметра
- регрессия, подогнанная к данным с учетом ограничений, не затрагивающих значения параметра  и
и
 ,
,
тогда F - статистика для проверки гипотезы  - имеет вид:
- имеет вид:

Критерий в такой форме обычно применяют для проверки гипотез  о не значимости параметра
о не значимости параметра 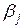 ; при выполнении этой гипотезы
; при выполнении этой гипотезы 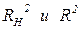 различаются незначительно.
различаются незначительно.
Каноническая форма модели
Каноническая форма модели  при гипотезе
при гипотезе  .
.
Пусть наша задача состоит в проверке гипотезы
 ,
,
для модели полного ранга  ; матрица
; матрица  размера
размера  ;
;  ;
;  , а
, а  - матрица размера
- матрица размера  ранга
ранга 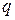 ;
; 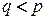 .
.
Поскольку матрица  имеет
имеет 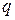 линейно независимых столбцов, можно без потери общности считать, что такими столбцами являются последние
линейно независимых столбцов, можно без потери общности считать, что такими столбцами являются последние 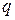 столбцов, т.е.
столбцов, т.е. 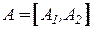 , где
, где  - невырожденная
- невырожденная 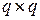 матрица. Разбивая соответствующим образом вектор
матрица. Разбивая соответствующим образом вектор  , получим:
, получим:




 .
.
Умножив обе части последнего равенства слева на  ,
,
получим:  . 3.19
. 3.19
С учетом (3.19) регрессия  может быть записана в каноническом виде:
может быть записана в каноническом виде:
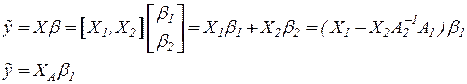 , 3.20
, 3.20
где 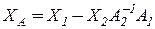
- матрица размера  с
с  линейно независимыми столбцами;
линейно независимыми столбцами;
матрица 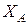 - полного ранга.
- полного ранга.
Предположим обратное: матрица 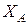 - имеет ранг меньше чем
- имеет ранг меньше чем  ; тогда найдется ненулевой вектор
; тогда найдется ненулевой вектор 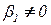 такой что:
такой что: 
из (3.20) 

 (т.к. матрица
(т.к. матрица 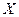 полного ранга) -
полного ранга) -  ;
;
из 

 ; возникшее противоречие означает, что равенство
; возникшее противоречие означает, что равенство  выполняется только при векторе
выполняется только при векторе  и
и 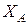 - имеет линейно независимые столбцы.
- имеет линейно независимые столбцы.
При решении МНК задачи о подборе зависимости  при наличии линейных ограничений
при наличии линейных ограничений 
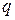 - параметров выражают через оставшиеся
- параметров выражают через оставшиеся  и сводят исходную задачу к задаче подбора модели с меньшим числом параметров
и сводят исходную задачу к задаче подбора модели с меньшим числом параметров  . Эту приведенную модель наблюдений
. Эту приведенную модель наблюдений  называют канонической.
называют канонической.
Задача о принадлежности двух выборок одной модели.
Пусть у нас имеются  наблюдений величин
наблюдений величин 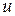 :
:  ,
,
представимых моделью 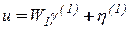 ; где
; где  матрица размера
матрица размера 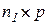 ранга
ранга  .
.
Пусть получено еще 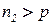 дополнительных данных, которые представимы
дополнительных данных, которые представимы
моделью:  , где
, где 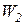 матрица размера
матрица размера  ранга
ранга  .
.
Требуется найти статистику для проверки гипотезы о том, что вторая выборка описывается той же моделью, что и первая, т.е.
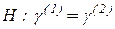 . 3.21
. 3.21
 ;
;  ;
;
Объединим обе группы наблюдений и запишем МНК-задачу определения оценок вектора  ;
;
 ;
; 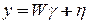 3.22
3.22
Поскольку в каждой из матриц  столбцы линейно независимы, матрица
столбцы линейно независимы, матрица 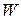 также имеет линейно независимые столбцы, т.е. имеет полный ранг -
также имеет линейно независимые столбцы, т.е. имеет полный ранг -  .
.
|
|
|
Гипотеза (3.21) о том, что обе группы данных описываются одной и той же моделью в задаче (3.22), есть:
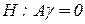 ;
;  , 3.23
, 3.23
а F - статистика для проверки гипотезы Н:
 , 3.24
, 3.24
Где  - остаточная сумма квадратов МНК-задачи с учетом ограничений (3.21), а
- остаточная сумма квадратов МНК-задачи с учетом ограничений (3.21), а 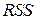 - без всяких ограничений. Для вычисления критерия (3.24) решим задачу МНК оценки параметров
- без всяких ограничений. Для вычисления критерия (3.24) решим задачу МНК оценки параметров 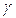 дважды: с учетом ограничений (3.21) и без них.
дважды: с учетом ограничений (3.21) и без них.
Решение задачи без ограничений (3.22) дает:  .
.
При наличии ограничений (3.23) приведем общую модель (3.23) к канонической форме:  3.25
3.25
и найдем 
Из (3.22)  ;
;
и 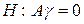 ;
; 




Обозначим решение задачи (3.25) -  , тогда:
, тогда:


В результате сравнения числа  c критической границей
c критической границей 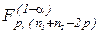 при заданном уровне значимости
при заданном уровне значимости 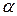 принимается или отвергается гипотеза Н о том, что обе выборки описываются одной и той же моделью. Если
принимается или отвергается гипотеза Н о том, что обе выборки описываются одной и той же моделью. Если  , то гипотеза о том, что обе выборки принадлежат одной и той же модели отклоняется.
, то гипотеза о том, что обе выборки принадлежат одной и той же модели отклоняется.
Замечание. Квантиль уровня ( ) распределения Фишера с 1 и k степенями свободы
) распределения Фишера с 1 и k степенями свободы  равен квадрату квантиля уровня (
равен квадрату квантиля уровня (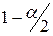 ) распределения Стьюдента с k степенями свободы:
) распределения Стьюдента с k степенями свободы:  .
.
Критерий Стьюдента.
Если гипотеза 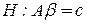 где
где 
 - матрица, отклонена, следует выяснить причину такого отклонения. С этой целью можно поочередно проверять каждую из гипотез
- матрица, отклонена, следует выяснить причину такого отклонения. С этой целью можно поочередно проверять каждую из гипотез  и выявить те из них, которые приводят к отклонению гипотезы Н; условия гипотезы
и выявить те из них, которые приводят к отклонению гипотезы Н; условия гипотезы 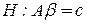 проверяем отдельно по каждой строке (здесь и далее
проверяем отдельно по каждой строке (здесь и далее  – строка матрицы
– строка матрицы  ). Возможный подход к решению этой задачи - продолжать применять
). Возможный подход к решению этой задачи - продолжать применять
 - критерий для проверки каждой
- критерий для проверки каждой  гипотезы. Однако задача имеет и более простое решение при использовании
гипотезы. Однако задача имеет и более простое решение при использовании 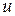 и
и  критериев.
критериев.
Вариант 1. Априорно известно значение 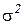 ;
;  . При этом случайная величина
. При этом случайная величина  имеет нормальное распределение
имеет нормальное распределение 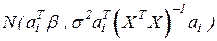 . Величину
. Величину  стандартизуют (центрируют и нормируют).
стандартизуют (центрируют и нормируют).
Если гипотеза  справедлива, стандартизованная величина:
справедлива, стандартизованная величина:
 3.26
3.26
 распределена нормально с нулевым средним и дисперсией 1.
распределена нормально с нулевым средним и дисперсией 1.
Критическая область значений  , при которых гипотеза
, при которых гипотеза  отвергается - область больших по модулю значений
отвергается - область больших по модулю значений  .
.
Критерий проверки гипотезы  :
:
если  . гипотеза
. гипотеза  отклоняется;
отклоняется;
здесь 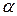 - уровень значимости критерия (вероятность ошибки 1-го рода – вероятность отклонить гипотезу в случае, когда она верна);
- уровень значимости критерия (вероятность ошибки 1-го рода – вероятность отклонить гипотезу в случае, когда она верна);
|
|
|
 - квантиль уровня
- квантиль уровня  или верхняя
или верхняя 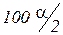 процентная точка нормального распределения.
процентная точка нормального распределения.
Вариант 2. 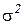 неизвестно и в критерии проверки гипотез
неизвестно и в критерии проверки гипотез  вместо величины
вместо величины  используют ее оценку
используют ее оценку  .
.
Если гипотеза  справедлива статистика:
справедлива статистика:
 3.27
3.27
имеет распределение Стьюдента с  степенями свободы (
степенями свободы ( - количество наблюдений,
- количество наблюдений,  - число оцениваемых параметров).
- число оцениваемых параметров).
Критерий проверки гипотезы  ;
;
если 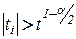 , то гипотеза
, то гипотеза  отклоняется; где
отклоняется; где 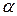 - уровень значимости, а
- уровень значимости, а  верхняя
верхняя  процентная точка распределения Стьюдента с
процентная точка распределения Стьюдента с  степенями свободы.
степенями свободы.
Приведенная процедура двухшаговой проверки гипотез (сначала применение F- критерия для выяснения справедливости гипотезы 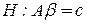 , а затем критерия (3.27) для проверки гипотез типа
, а затем критерия (3.27) для проверки гипотез типа  ) называется критерием минимальной значимости разности - LSD. Употребление в критерии слова "разность" связано с тем, что LSD -критерий обычно используют для сравнения параметров, например, для сравнения средних значений совокупностей методом парных сравнений. Достоинство метода в простоте и гибкости. Недостаток в том, что возможны случаи, когда гипотеза Н отвергается, а все гипотезы
) называется критерием минимальной значимости разности - LSD. Употребление в критерии слова "разность" связано с тем, что LSD -критерий обычно используют для сравнения параметров, например, для сравнения средних значений совокупностей методом парных сравнений. Достоинство метода в простоте и гибкости. Недостаток в том, что возможны случаи, когда гипотеза Н отвергается, а все гипотезы  принимаются.
принимаются.
Замечание. В статистических пакетах (Statgrafic) в качестве результата проверки выдают величину уровня значимости, соответствующего вычисленному значению критерия - significal level  и,
и,
если 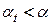 , гипотеза
, гипотеза  отвергается, если
отвергается, если  - принимается.
- принимается.
3.4 Построение доверительных интервалов для линейных комбинаций параметров и значений регрессии.
Доверительный интервал для величины  , где a - постоянный вектор (например,
, где a - постоянный вектор (например,  – строка матрицы
– строка матрицы  ), а
), а  вектор параметров модели данных
вектор параметров модели данных  строится на основе оценок
строится на основе оценок 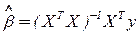 и оценок
и оценок  дисперсии наблюдений
дисперсии наблюдений 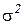 :
:
 3.28
3.28
Интервал со случайными границами (3.28) с вероятностью  , накрывает оцениваемую величину
, накрывает оцениваемую величину  .
.
Здесь  верхняя
верхняя  процентная точка распределения Стьюдента, а s - выборочное стандартное отклонение ошибок наблюдений.
процентная точка распределения Стьюдента, а s - выборочное стандартное отклонение ошибок наблюдений.
Пользуясь (3.28) можно, например, построить доверительный интервал для значения регрессии  в любой точке -
в любой точке - 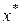 . Для этого записывают вектор
. Для этого записывают вектор  , компоненты которого равны значениям регрессоров
, компоненты которого равны значениям регрессоров  в выбранной точке
в выбранной точке 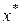 –
–
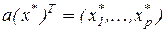 или
или  .
.
Доверительный интервал с вероятностью  , накрывающий величину
, накрывающий величину  есть:
есть:

Построение совместных доверительных интервалов для величин  ;
;  .
.
Совместное интервальное оценивание  - линейных комбинаций
- линейных комбинаций  ;
;  представляет собой довольно сложную статистическую проблему.
представляет собой довольно сложную статистическую проблему.
Если воспользоваться (3.28) и построить  доверительных интервалов с границами
доверительных интервалов с границами
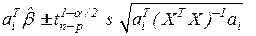 ,
,  3.29
3.29
для величин  с вероятностью
с вероятностью  каждый
каждый
 ,
,
то вероятность того, что эти утверждения будут выполняться одновременно для всех  интервалов может отличаться от
интервалов может отличаться от  .
.
|
|
|
Действительно, пусть 
 - событие, состоящее в том, что
- событие, состоящее в том, что
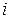 -ое доверительное утверждение верно, и вероятность события
-ое доверительное утверждение верно, и вероятность события  -
-  тогда, если
тогда, если  - событие дополнительное к
- событие дополнительное к  , то
, то 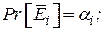


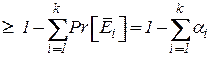 3.30
3.30
Если все  одинаковы
одинаковы 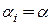 ,
,
то  ;
;  ; 3.31
; 3.31
и вероятность того, что все  доверительных утверждений
доверительных утверждений  верны, находится в диапазоне
верны, находится в диапазоне  . Например, если
. Например, если 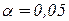 , а
, а 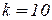 , то
, то 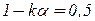 , т.е. с вероятностью большей 0,5 все 10 утверждений о доверительных границах (3.29) справедливы. Равенство в (3.31) слева достигается при независимости событий
, т.е. с вероятностью большей 0,5 все 10 утверждений о доверительных границах (3.29) справедливы. Равенство в (3.31) слева достигается при независимости событий  .
.
Если каждому из  доверительных интервалов задать уровень значимости равный
доверительных интервалов задать уровень значимости равный 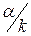 и расширить их границы, то из (3.31) получаем:
и расширить их границы, то из (3.31) получаем:
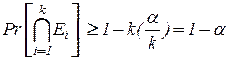 и тем самым достигается желаемая вероятность выполнения всех
и тем самым достигается желаемая вероятность выполнения всех  доверительных ограничений. (Интервалы Бонферрони).
доверительных ограничений. (Интервалы Бонферрони).
|
|
|


