 |
Процедуры MatLab подбора регрессий.
|
|
|
|
Пакет прикладных программ MatLab содержит процедуры вычисления регрессий в двух разделах: Statistics Toolbox и Curve fitting Toolbox.
В разделе Statistics Toolbox приведены следующие процедуры подбора линейных регрессий:
b = regress(y,X) returns the least squares fit of y on X by solving the linear model for 
, where: b is an estimate of 
; y is an n-by-1 vector of observations; X is an n-by-p matrix of regressors; is a p-by-1 vector of parameters; 
is an n-by-1 vector of random disturbances
[b,bint,r,rint,stats] = regress(y,X) returns an estimate of 
in b, a 95% confidence interval for in the p-by-2 vector bint. The residuals are returned in r and a 95% confidence interval for each residual is returned in the n-by-2 vector rint. The vector stats contains the 
statistic along with the F and p values for the regression.
[b,bint,r,rint,stats] = regress(y,X,alpha) gives 100(1 - alpha)% confidence intervals for bint and rint. For example, alpha = 0.2 gives 80% confidence intervals. X should include a column of ones so that the model contains a constant term. The F statistic and p value are computed under the assumption that the model contains a constant term, and they are not correct for models without a constant. The R -square value is one minus the ratio of the error sum of squares to the total sum of squares. This value can be negative for models without a constant, which indicates that the model is not appropriate for the data.
Раздел Curve fitting Toolbox.
Curve fitting refers to fitting curved lines to data. The curved line comes from regression techniques, a spline calculation, or interpolation. The data can be measured from a sensor, generated from a simulation, historical, and so on. The goal of curve fitting is to gain insight into your data. The insight will enable you to improve data acquisition techniques for future experiments, accept or refute a theoretical model, extract physical meaning from fitted coefficients, and draw conclusions about the data's parent population.
Parametric fitting produces coefficients that describe the data globally, and often have physical meaning. Fit your data using parametric models such as polynomials and exponentials, specify fit options such as the fitting algorithm and coefficient starting points, and evaluate the goodness of fit using graphical and numerical techniques
Parametric fitting involves finding coefficients (parameters) for one or more models that you fit to data. The data is assumed to be statistical in nature and is divided into two components: a deterministic component and a random component.
data = deterministic component + random component
The deterministic component is given by the fit and the random component is often described as error associated with the data.
data = fit + error
The fit is given by a model that is a function of the independent (predictor) variable and one or more coefficients. The error represents random variations in the data that follow a specific probability distribution (usually Gaussian). The variations can come from many different sources, but are always present at some level when you are dealing with measured data. Systematic variations can also exist, but they can be difficult to quantify.
|
|
|
The fitted coefficients often have physical significance.
For example, suppose you have collected data that corresponds to a single decay mode of a radioactive nuclide, and you want to find the half-life (T1/2) of the decay. The law of radioactive decay states that the activity of a radioactive substance decays exponentially in time.
Therefore, the model to use in the fit is given by 
where 
is the number of nuclei at time t = 0, and 
is the decay constant. Therefore, the data can be described by: + error
Both and are coefficients determined by the fit. Because T1/2 = ln(2)/ , the fitted value of the decay constant yields the half-life. However, because the data contains some error, the deterministic component of the equation cannot completely describe the variability in the data. Therefore, the coefficients and half-life calculation will have some uncertainty associated with them. If the uncertainty is acceptable, then you are done fitting the data. If the uncertainty is not acceptable, then you might have to take steps to reduce the error and repeat the data collection process.
Nonparametric fitting is useful when you want to fit a smooth curve through your data, and you are not interested in interpreting fitted coefficients.
Fit your data using nonparametric fit types such as splines and interpolants.
4. Выбор матрицы плана при планировании экспериментов.
В основном точность оценивания по методу наименьших квадратов определяет матрица плана 
, например,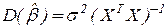 
. Поэтому в случаях, когда нам предоставлена возможность самим организовать эксперимент, следует позаботиться о том, чтобы результаты оценивания по МНК были наилучшими в том или ином смысле.
Пусть мы планируем эксперимент для определения линейной связи 
переменных 
и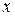 
; причем независимую переменную можно варьировать в пределах от 
до 
. Всегда можно стандартизовать нашу задачу приведением интервала 
к интервалу 
, используя линейное преобразование:
; (Обратная замена: 
) 4.1
Далее будем считать, что такое приведение выполнено и всегда: .
Для построения прямой, отражающей связь между переменными и 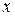достаточно двух точек.
Разместим эти две точки 
и 
на краях интервала ;
т.е. 
; 
;
Наблюдениям в этих точках соответствует матрица плана 
; Дисперсионная матрица оценок параметров 
задачи 
есть: 
.
|
|
|
Предложенный план эксперимента при двух наблюдениях 
дает одинаковые дисперсии оценок параметров : 
и 
.
Увеличим число наблюдений до 4 
и рассмотрим эффекты нескольких вариантов размещения точек на том же интервале.
План А
На интервале 
наблюдения проводятся в крайних точках 
Увеличение числа наблюдений вдвое, вдвое уменьшило дисперсии оценок параметров .
План Б1
На интервале наблюдения проводятся в точках 
:
определяется с прежней точностью 
, а 
- хуже - ..
План Б2
На интервале наблюдения проводятся в точках 
:
определяется с прежней точностью , а - еще хуже - 
.
План Б3
На интервале наблюдения проводятся в точках 
:
Здесь оба параметра оцениваются с большей дисперсией, чем в лучшем пока варианте – плане А, кроме того появилась корреляция между оценками.
План Б4
На интервале наблюдения проводятся в точках 
:
;
Сближение точек наблюдения приводит к тому, что оценивается чуть хуже, чем в лучшем плане А, а оценивается раз в 40 хуже; кроме того, опять присутствует корреляция между оценками.
План Б5
На интервале наблюдения проводятся в точках 
:
Ранг матрицы плана равен 1, и матрицы обратной 
не существует; параметр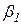 
оценить не удается.
Итак, наилучшие в смысле малости дисперсий оценок параметров линейной модели результаты достигаются при размещении наблюдений по краям интервала допустимых значений 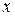. Сближение точек наблюдений приводит к увеличению дисперсий оценок 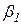. Асимметрия в наблюдениях вызывает появление корреляций оценок.
Посмотрим, как следует размещать наблюдения, если планы сравнивать по дисперсии прогноза.
Прогноз в точку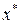 
зависит от плана , используемого при построении оценок вектора параметров модели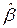 
, и вычисляется как: 
; 
; дисперсия такого прогноза равна: 
..
Вычислим дисперсию прогноза в точки, расположенные как внутри, так и вне интервала . Для примера, если при оценке параметров модели использовался план А, (соответственно матрица ); если прогноз вычисляется в точку 
, то 
; и дисперсия (вариация) прогноза равна 
В таблице приведены относительные вариации 
прогнозов в точки 
для различных вариантов размещения наблюдений:
|
|
|
| xi | 0 | 1/2 | 1 | 1.5 |
| A | 1/4 | 5/16 | 2/4 | 13/16 |
| Б1 | 1/4 | 3/8 | 3/4 | 11/8 |
| Б2 | 1/4 | 1/2 | 5/4 | 10/4 |
| Б3 | 1/3 | 1/4 | 1/3 | 7/12 |
Для планов - А, Б1, Б2, имеющих симметричное относительно нуля размещение точек наблюдений, дисперсия прогноза увеличивается c удалением точки прогноза от нуля. Наилучший прогноз в точку вне интервала наблюдений 
в варианте Б3, в котором наблюдения сгруппированы на правой границе интервала.
Итак, параметры линейной модели оцениваются с наибольшей точностью, если наблюдения располагать на краях интервала. Прогнозы за интервал наблюдения имеют меньшие дисперсии, если часть наблюдений выполнена в граничной точке, расположенной ближе к прогнозируемой точке. Планы экспериментов следует выбирать в зависимости от требований решаемых задач.
4.1 Ортогональная структура матрицы плана.
В задаче МНК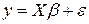 
; - матрица размера 
, ранга 
(матрица полного ранга).
= 
, 4.1
здесь 
- 
-ый столбец матрицы ; матрица и вектор записаны как блочные матрицы.
Предположим, что матрица имеет ортогональные столбцы –
, 
, тогда
1. Если матриц плана, имеет ортогональные столбцы, все коэффициенты 
оцениваются независимо друг от друга.
2. 
, если после подбора параметров производится проверка их значимости, то при проверке гипотезы 
не требуется заново вычислять 
; его можно найти как: 
.
Итак, если матрица плана имеет ортогональные столбцы, существенно упрощаются расчеты, связанные с вычислением оценок и проверкой гипотез типа .
Теорема Хоттелинга. Если матрица плана в задаче МНК 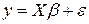; такова, что 
, то: 
4.2
Равенство достигается в случае, если матрица плана ортогональна.
Итак, наилучшим планом в смысле малости дисперсий оценок компонент вектора , является ортогональный.
4.2 Понятие оптимального плана.
В задаче МНК ;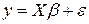 
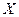- матрица плана размера 
;
- - мерный вектор параметров.
Совокупность величин 
называют планом эксперимента.
Здесь: 
- общее количество наблюдений,
- общее число неповторяющихся комбинаций 
значений регрессоров; - опорные точки,
- точка в - мерном пространстве допустимых значений регрессоров; 
,
|
|
|
- число наблюдений в точке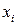 
; 
- вес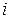 
-го наблюдения;
; 
.
Качество выполняемых расчетов, связанных с МНК в значительной степени определяется матрицей 
, которую называют информационной. Естественно матрица 
есть функция плана 
.
В частности дисперсионная матрица МНК-оценок: 
зависит от плана.
Мы будем называть оптимальным план, минимизирующий (максимизирующий) некую функцию информационной матрицы 
. Так как матрица не зависит от оцениваемых параметров, то имеет смысл говорить об априорном поиске планов, минимизирующих заданную функцию
4.3
На множестве допустимых планов 
вычисляются значения , тот план или те планы 
, которые доставляет наименьшее значение – называют оптимальными.
Задачу (4.3) поиска экстремума критерия 
называют задачей оптимального планирования эксперимента по критерию .
Планы, в которых 
называют сингулярными, если 
- регулярными. Аналитически выбрать план (4.3) удается только для некоторых простейших задач регрессионного анализа.
-оптимальные планы
- оптимальным называется план , который выбирается по правилу:
4.4
Оптимальный план (4.4) доставляет минимум объему эллипсоида рассеяния НЛН – оценок параметров задачи МНК 
, если ошибки 
;
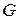-оптимальные планы
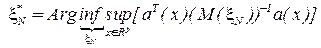4.5
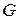-оптимальные планы, в области 
допустимых точек прогноза, минимизируют максимальное значение дисперсии оценки функции регрессии и гарантируют построение наиболее узких доверительных границ при всех .
-оптимальные планы
4.6
-оптимальные планы минимизируют величину среднего риска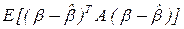 
при обобщенных квадратичных потерях 
из-за ошибок оценивания ,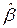 
- заданная положительно определенная матрица.
-оптимальные планы
4.7
-оптимальные планы, в области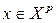 
, минимизируют среднее значение дисперсии оценки функции регрессии.
Для всех упомянутых типов оптимальности структура планов такова, что опорные точки следует выбирать на границах области задания. (Ермаков СМ, Планирование эксперимента, стр51.)
Полиномиальная регрессия
В множественной регрессии 
5.1
регрессоры 
могут быть функциями других переменных, например 
:
u0 = u0 (х, z)
...
up = up (х, z)
МНК накладывает определенные ограничения на эти функции. Для того чтобы существовала единственная МНК оценка 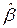необходимо, чтобы функции 
на множестве значений независимых переменных 
, при которых производятся наблюдения y, составляли систему линейно независимых векторов.
Выбор регрессоров как степенных функций одной переменной :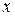
приводит к полиномиальной регрессии:
5.2
или в матричном виде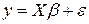
для наблюдений 
в точках 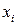при i=1,n;
где матрица плана: 
Если матрица в выражении для оценки 
плохо обусловлена, возможны существенные вычислительные ошибки при нахождении 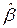и большие значения дисперсий отдельных компонент вектора .
|
|
|
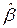Оказывается, что эффекты плохой обусловленности матрицы сказываются при полиномиальной регрессии уже при степенях 
. Уйти от плохой обусловленности можно понизив степень полинома. Однако не во всякой задаче это возможно.
Существуют и другие подходы, позволяющие проводить надежные вычисления 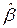при достаточно высоких степенях полинома .
Первый прием: приведение множества точек, в которых проводятся наблюдения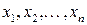 
к диапазону (-1,1). Как правило, такое преобразование приводит к появлению “нулей” в матрице и уменьшению ошибок при ее обращении.
Интервал 
приводят кинтервалу , используя линейное преобразование:
;
(Обратная замена: 
)
Второй прием заключается в выборе в качестве регрессоров функций 
более сложных, чем просто степенные: их выбирают так, чтобы на множестве точек 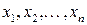столбцы матрицы были ортогональны.
; 
,
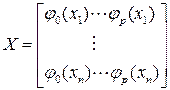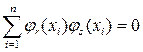и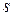 
- любые числа от 0 до .
|
|
|
