 |
Процедура Форсайта получения ортогональных полиномов.
|
|
|
|
На любом наборе различных точек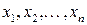 
можно построить систему ортогональных полиномов до k-го порядка включительно. Для этого набор точек 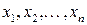приводится к стандартному виду – к точкам на интервале [-1,1], а затем используется рекуррентная процедура Форсайта построения ортогональных полиномов.
; 
;
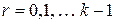Здесь: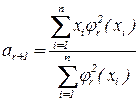 
; 
;
; 
.
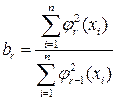Для каждого набора точек 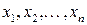, т.е. для каждой новой задачи, строится своя система полиномов 
.
Построение ортогональных полиномов на системе
Равноотстоящих точек.
Система равноотстоящих точек 
, где 
- нечетное, линейным преобразованием может быть приведена к системе целочисленных точек с единичным шагом:
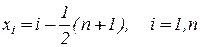5.3
На системе n точек (5.3) могут быть определены ортогональных полиномов со степенями от нулевой до (
).
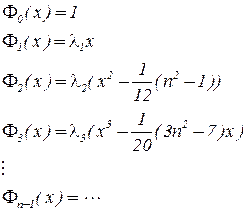5.4
В (5.4) коэффициенты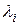 
выбираются так, чтобы все полиномы 
имели на множестве (5.3) целочисленные значения. Такой выбор функций позволяет сократить вычислительные ошибки при расчете МНК-оценок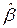 
за счет выполнения части операций в «целочисленной арифметике».
Полиномы (5.4) носят название полиномов Чебышева. При изменении числа точек в наборе (5.3), полиномы (5.4) должны вычисляться заново.
Регрессия на ортогональных полиномах.
При построении полиномиальной регрессии в качестве регрессоров выберем ортогональные на множестве значений независимой переменной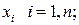 
полиномы: 
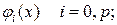тогда модель связи 
есть:
;
;
; 
,
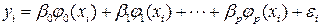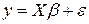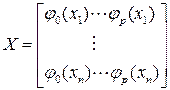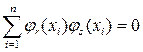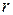и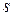 
- любые числа от 0 до 
.
При этом матрица: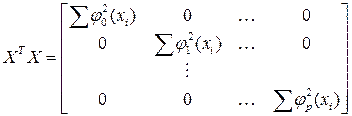 
оказывается диагональной и оценки для параметра 
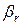находятся независимо от других:
, 
, т.к. обычно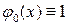 
и имеют в соответствии с теоремой Хоттелинга минимальную дисперсию.
Остаточная сумма квадратов.
При решении задачи подбора наилучшей регрессии применение ортогональных полиномов позволяет существенно упростить проверку значимости отдельных регрессоров.
|
|
|
Действительно, если мы проверяем гипотезу 
, то в критерии
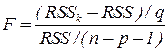
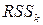(остаточная сумма квадратов при выполнении гипотезы 
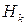) находится удалением k -го слагаемого из суммы 
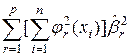в выражении для 
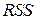, т.е.
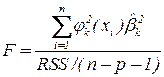
Если 
велико и превышает критическую границу, то коэффициент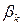 
оставляют, иначе – удаляют. Чтобы проверить значимость всех коэффициентов задачу оценки параметров 
по МНК решают всего 1 раз.
Оптимальное расположение точек при полиномиальной
Регрессии.
Задача подбора полинома степени является одной из немногих задач, в которых решена проблема выбора оптимального расположения точек наблюдения.
Пусть переменная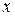 
преобразована так, что все ее возможные значения принадлежат интервалу [-1, 1].
Оптимальное размещение точек наблюдения на интервале [-1, 1] зависит от цели, которую мы преследуем при подборе полинома.
Если решается задача интерполяции таблицы наблюдений (например, по таблице строится калибровочная кривая), оптимально одно расположение точек; если нас интересуют непосредственно сами коэффициенты регрессии (все или любая их часть), оптимален другой план, если по таблице наблюдений строится прогноз (задача экстраполяции), – третий.
Задача интерполяции.
Цель выбора оптимального расположения точек: минимизировать дисперсию регрессионной кривой (5.2) на всем интервале изменения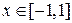 
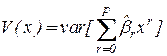
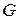- оптимальный план, реализует минимаксную стратегию выбора наилучшего плана: 
.
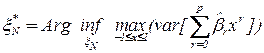Для каждого плана на интервале [-1, 1] находится точка с максимальным значением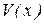 
; из всех возможных планов 
выбирают тот, для которого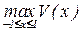 
принимает минимальное значение.
В задачах построения интерполяционной кривой на основе полинома (5.2) план таблицы наблюдений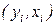 
таков, что 
приведен к диапазону [-1, 1].
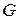- оптимальным является следующий план:
1. Наблюдения выполняются в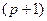 
различных точках 
,
|
|
|
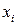2. Все точки имеют одинаковый вес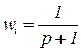 
,
3. Точки 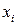выбираются как нули функции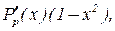 
где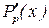 
- производная полинома Лежандра p - й степени, т.е. 
.
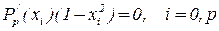При таком оптимальном выборе плана дисперсия регрессионной кривой во всех узловых точках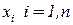 
, одинакова и равна:
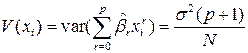, где 
- общее количество наблюдений.
|
|
|
