 |
Нелинейные модели, приводимые к линейным относительно параметров.
|
|
|
|
;
;
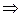
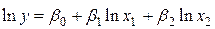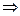
МНК оценивание коэффициентов связанных линейных
Уравнений.
В общем случае уравнения системы:
, 1.13
где g и a - параметры, подлежащие определению, 
- переменные, определяющие поведение системы;
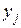– j - ая эндогенная переменная (j=1,n),
xi – i -ая экзогенная переменная (i=1,m).
Эндогенные переменные зависят от остальных переменных: от всех или некоторых из них, а экзогенные - нет.
Структурная форма модели системы (1.13) создается в процессе формализации причинно-следственных связей в системе.
Структурных коэффициентов 
в системе не больше, чем
n·(n-1+m) штук.
Использование обычного МНК для оценивания структурного уравнения каждого в отдельности приводит к смещенным и несостоятельным оценкам.
В матричном виде структурную модель системы можно записать как:
Если существует 
(матрица обратная 
), т.е. – не вырождена, то система может быть приведена к виду:
1.14
Это приведенная форма модели системы.
В выражении (1.14) отсутствуют взаимосвязи между отдельными эндогенными переменными; каждая эндогенная переменная 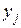выражена только через экзогенные переменные.
Если для каждого j имеются таблицы совместных наблюдений
;
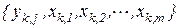
эндогенных переменных 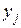и экзогенных переменных 
то, пользуясь МНК можно получить оценки параметров модели (1.14) для каждой эндогенной переменной по отдельности (минимальное число наблюдений для подбора 
параметров 
линейных регрессий задачи (1.14) может быть всего 
).
После того, как параметры приведенной модели (элементы матрицы B) получены, возникает проблема обратного перехода к структурной форме модели. Из системы алгебраических уравнений 
следует найти элементы матриц Г и А.
|
|
|
Переход к описаниям в естественном (исходном) виде.
Количество параметров, которое оценивается по приведенной модели равно 
.
В исходной структурной схеме их может быть n·(n-1+m) штук, т.е. больше, чем мы определили на основе (1.14).
Единственным образом эту задачу не решить.
Между матрицами приведенной и исходной формы уравнений системы существует связь:
Þ 
Þ ГВ· + A = 0; 1.15
Обычно часть элементов матриц Г и А априорно известна.
Например, если связи между парой переменных 
нет, то соответствующий элемент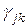 
матрицы есть 0, а если связь полная, то 1.
Если после подобных назначений уравнения (1.15) однозначно разрешаются, то система (1.13) идентифицируема и поставленная задача решена; если число параметров 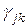и 
, которые следует определить больше числа (), задача построения регрессий (1.13) не разрешима, в противном случае говорят, что задача переопределена и используют, так называемый, двухшаговый МНК.
Двухшаговый МНК.
1. На первом шаге используют МНК, чтобы получить оценки 
из приведенной (1.14) системы уравнений.
2. На втором шаге для каждого из структурных уравнений по МНК находят оценки варьируемых параметров g и a, подставив в правые части уравнений (1.13) вместо эндогенных переменных их оценки .
Недостаток оценивания коэффициентов взаимозависимых линейных уравнений в неединственности решений (результат оценивания зависит от порядка в котором решаются уравнения), необходимости обращения матриц и связанное с этим накопление ошибок.
Только краткосрочные прогнозы относительно достоверны.
Пример. Первая модель Клейна процесса формирования экономики государства (США между мировыми войнами). Коэффициенты линейных уравнений, приведенных ниже, были определены на основе избыточных наблюдений с использованием двухшагового МНК.
Уравнения поведения отдельных экономических единиц или групп:
1. Функция потребления
|
|
|
С = 16,8 + 0,02Р + 0,23Р-1 + 0,80(W1 + W2) + uc, где
С – потребление
Р – прибыль
Р-1 – прибыль прошлого года
W1 – заработная плата в частном секторе
W2 – заработная плата в государственном секторе
uc – погрешность функции потребления
Все переменные указаны в млрд. долларов.
2. Функция инвестиций
I = 17,8 + 0,23Р + 0,55Р-1 - 0,15K-1 + uI, где
I – частные инвестиции
Р – прибыль
Р-1 – прибыль прошлого года
K-1 – основной капитал на начало года
uI – погрешность функции инвестиций
3. Уравнение спроса на труд
W1 = 1,6 + 0,42Х + 0,16Х-1 + 0,13(t – 1931) + uW, где
W1 – заработная плата в частном секторе
X – продукция частного сектора
X-1 – продукция частного сектора за прошлый год
0,13 – усиление позиций рабочих при заключении трудовых договоров
1931 – год, с которого началось исследование
uW – погрешность уравнения спроса на труд
Определяющие уравнения:
4. X = C + I + G, где
X – продукция частного сектора
С – на потребление
I – на инвестиции
G – покупается государством
5. P = X - W1 - T, где
P – прибыль
W1 – заработная плата
T – налоги
6. K = K-1 + I, где
K – основной капитал
K-1 – основной капитал на начало года
I – инвестиции
В приведенной модели шесть уравнений и десять переменных.
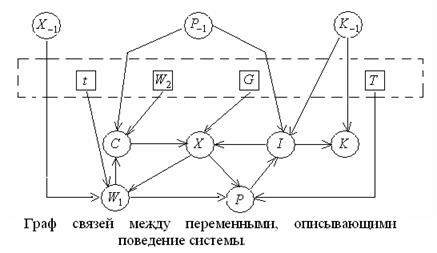
Четыре переменные – особые, три из них контролируются государством: W2, T, G, а четвертая – t вообще не зависит от экономики.
Эти переменные по отношению к системе являются экзогенными (независимыми). Остальные – эндогенные (зависимые).
В нашем примере (модель Клейна) всех коэффициентов g и a - 12 штук, экзогенных переменных m=4, эндогенных переменных n=6. После решения приведенной системы (1.14) мы имеем 
соотношений, связывающих значения элементов матриц Г,А и В; в системе (1.15) больше связей, чем требуется для однозначного определения коэффициентов g и a. Коэффициенты уравнений Клейна получены на основе приведенного выше двухшагового МНК.
|
|
|
