Статистические свойства МНК оценок

 

МНК решает задачу подбора параметрической зависимости

; 2.1

на основе таблицы наблюдений

; , 2.2

где - значение -го регрессора в 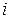-ом наблюдении; ,

- подбираемые параметры.

Oбычно модель (2.1) содержит регрессор 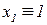(модель содержит постоянную составляющую); регрессорами могут быть и заданные функции переменной , любой из списка (2.2).

Наблюдение 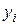в (2.2) при модели данных (2.1) есть:

2.3

или в матричной форме:

; при модели данных ; ; 2.4

где - - вектор ошибок наблюдений и подгонки,

 

а - матрица плана размера ; ; ранга ,

если в качестве модели таблицы наблюдений ; ; выбирается , где регрессорами являются функции переменной 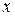, то векторы значений этих функций на множестве значений регрессоров должны быть взаимно линейно независимы.

Матрицы в этом случае есть: , и линейная независимость векторов значений функций на множестве значений регрессоров означает линейная независимость столбцов матрицы и полный ранг матрицы .

При любом выборе регрессоров в модели (2.1) ее решение по методу наименьших квадратов находят как:

, 2.5

- оценка вектора параметров модели данных (2.1).

Используем аппарат математической статистики для исследования ошибок аппроксимации таблицы наблюдений (2.2) при построении линейной регрессии (2.1).

--------------------------------------------------------------------------------------------

Замечание 1. О вычислении математического ожидания случайной матрицы.

Пусть - совокупность случайных величин, имеющих математическое ожидание , тогда по определению математическое ожидание матрицы 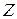с элементами равно . Если - постоянные матрицы, то , здесь - знак математического ожидания, 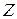- случайная матрица, размерности матриц таковы что операции умножения допустимы.

Если случайные векторы, то 2.6

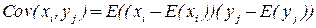
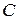Ковариационной матрицей случайных векторов размерности и называют матрицу размера с элементами : .

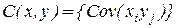Если , ковариационная матрица носит название дисперсионной матрицы вектора .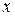

Дисперсионная матрица вектора 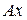, где - неслучайная матрица, а 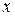- случайный вектор, равна: . 2.7

, где - постоянный вектор.

Математическое ожидание квадратичной формы:

2.8 Здесь 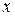- случайный вектор, - матрица коэффициентов квадратичной формы,

- след произведения матриц и ;

и - соответственно математическое ожида­ние и дисперсионная матрица случайного вектора .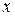

Следом квадратной матрицы называют сумму ее диагональных элементов -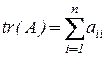

--------------------------------------------------------------------------------------------

Предположим, что:

1- значения регрессоров в таблице наблюдений ; известны точно; значения зависимой переменной 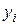искажены ошибками , в которые входят ошибки измерений и возможно ошибки аппроксимации,

2 - зависимость (2.1) истинна,

3 - ошибки наблюдений - независимые случайные величины, имеющие одинаковые распределения.

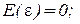
; 2.9

здесь и далее - единичная матрица размера ().

Предположение означает, что модель истинна и не имеет систематических ошибок. Ошибки в этом случае называют несмещенными.

Т.к. - случайный вектор, то и - оценка вектора параметров - случайный вектор; кроме того, из (2.4), (2.6) и (2.9) следует .

 

Вычислим основную характеристику оценки - ее математическое ожидание:

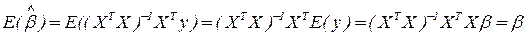
Оценка по методу наименьших квадратов в предположениях (2.9) является несмещенной, т.е. математическое ожидание равно самой .

А теперь найдем дисперсионную матрицу оценок , которая характеризует степень рассеяния оценок относительно математического ожидания.

Из 2.9 следует: ,

и вследствие (2.7) дисперсионная матрица

оценок равна:

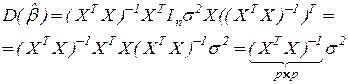
Здесь использовано то, что матрицы и 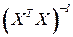- симметричны и транспонирование этих матриц не меняет их значений т.е. .

На главной диагонали дисперсионной матрицы размера () находятся дисперсии оценок параметров модели данных. Недиагональные элементы определяют корреляционную связь между оценками параметров и , где .

Оказывается, что оценки по методу наименьших квадратов являются наилучшими в классе линейных, несмещенных оценок, т.е. оценок представляющих собой линейную комбинацию наблюдений (данных),

 

Теорема Маркова

Пусть - оценка по методу наименьших квадратов вектора . Тогда в классе всех линейных несмещенных оценок линейной комбинации оценка является единственной оценкой, обладающей наименьшей дисперсией.

При этом говорят, что является наилучшей, линейной, несмещенной оценкой (оценкой НЛНО).

Для доказательства мы должны сравнить между собой дисперсии оценки и какой-либо другой линейной, несмещенной оценки для .

 

Доказательство.

, где - матрица подгонки (матрица проектирования вектора на подпространство , порожденное столбцами матрицы ;

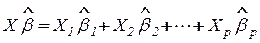Из ; любой - мерный вектор преобразованием переводится в , т.е. представляется как элемент подпространства (проектируется на подпространство , порожденное столбцами матрицы )

; ;

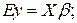
Замечание 2. Свойства матрицы : 2.10

Матрица симметрична, имеет размер , ранг (ранг произведения матриц не превосходит ранга сомножителей).

Матрица идемпотентна. Любая степень идемпотентной матрицы равна самой себе (например, единичная матрица идемпотентна); и . Действительно:

и

;

След идемпотентной матрицы равен ее рангу ;

-------------------------------------------------------------------------------------------------

Вычислим математическое ожидание оценки , учитывая приведенные свойства матрицы :

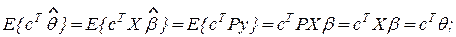
Здесь 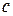- неслучайный вектор, - неслучайная матрица.

Итак, для всех ( - линейная комбинация столбцов матрицы ) т.е. является несмещенной оценкой величины .

Рассмотрим какую-нибудь другую линейную, несмещенную оценку для ;

- неслучайный вектор, - вектор наблюдений.

Из и

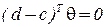
Т.е. скалярное произведение - мерных векторов и равно нулю.

Если векторы () и имеют нулевое скалярное произведение, то вектор () перпендикулярен вектору . Вектор принадлежит подпространству . Проекция вектора () на равна нулю и как следствие ; .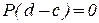

Сравним дисперсии оценок и . Сравниваемые величины скалярные. Имеем:

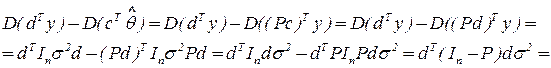
= 0

Заметим, что матрица идемпотентна, тогда как (матрица не идемпотентна).

- это квадрат длины вектора ) и является неотрицательной величиной.

Знак равенства достигается когда , при этом альтернативная оценка превращается в . Итак, МНК-оценка в классе всех линейных несмещенных оценок величины является единственной оценкой с минимальной дисперсией.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: