 |
Задача о сравнении средних двух независимых нормальных выборок.
|
|
|
|
Пусть заданы выборки из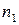 
элементов 
; 
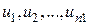; и 
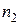элементов 
; 
.
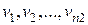Цель исследования - сравнить выборки на предмет обнаружения различия в их средних.
Формализуем задачу как задачу МНК.
; 
; 
; 
;
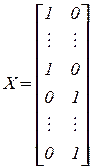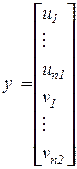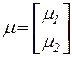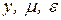- соответственно объединенные векторы наблюдений, параметров, ошибок.
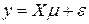
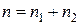
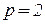
Оценки находят как:
;
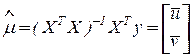где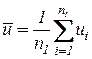 
; 
; 
.
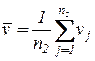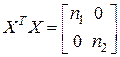Проверим гипотезу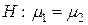 
о равенстве средних исследуемых выборок.
; 
, 
; 
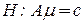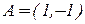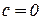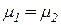
Вычислим статистику 
:
; 
;
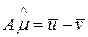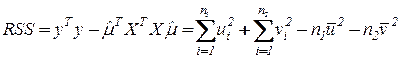Отсюда: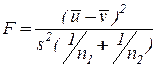 
. Сравнением с критической границей 
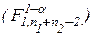и проверяем справедлива или нет гипотеза 
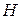: если 
, то гипотеза 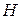: 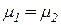справедлива при уровне значимости 
.
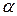Рассмотренная задача является основной для дисперсионного анализа. Задача может быть решена и при любом числе выборок.
Примеры: Контроль старения измерительного средства: в первой выборке результаты поверки ИС прошлого года во второй – текущего; наблюдения по спросу на продукт до рекламы и после рекламы; проверка эффективности применения нового лечебного препарата – одной группе больных вводят препарат, другой нет. Во всех случаях интересуются наличием различий в средних сравниваемых выборок.
Задача взвешивания.
Имеется две группы однородных предметов, необходимо найти средний вес предметов в каждой группе и сравнить их. Под взвешиванием можно понимать как собственно взвешивание, так и процедуры определения других характеристик предмета. Оказывается, что взвешивание по отдельности предметов и вычисление затем средних весов в каждой группе не лучшая стратегия в организации наблюдений.
Рассмотрим вариант определения средних весов однотипных предметов двух различных групп и их сравнения на основе МНК. Предметы каждой группы одинаковы; допустимый производственный разброс весов предметов в обеих группах одинаков и характеризуется дисперсией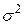 
.
|
|
|
Вес предмета первой группы есть: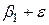 
, второ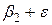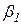й - 
; 
и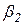 
- средние веса предметов первой и второй группы, 
- производственный разброс. Есть основание считать, что весы, на которых производится взвешивание, исправны и не имеют систематических ошибок; ошибки собственно взвешивания пренебрежимо малы по сравнению с рассеянием весов исследуемых предметов; отклонения весов предметов от средних значений - независимые случайные величины.
Далее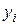 
- показания весов при 
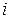измерении. Выполним 
измерений.
При первом измерении на чашке 1 весов - гири, а на чашке 2 предмет 1-ой группы:
; 
; 3.7
Во втором измерении: на чашке 1 гири и один элемент из второй группы,
а на чашке 2 - два предмета первой группы:
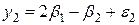
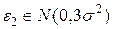
При третьем измерении на чашке 1 – гири, а на чашке 2 –один предмет первой группы и два предмета второй:
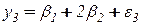
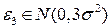3.8
Применим обобщенный метод наименьших квадратов для нахождения 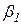и 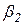- на основе уравнений (3.7 – 3.8).
;
; 
, 
;
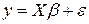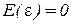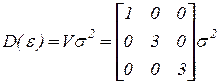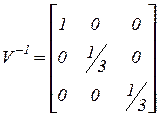- матрица плана; составляется из значений регрессоров (коэффициентов при параметрах) для всех измерений.
В нашем случае:
; 
; 
;
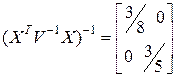Оценки средних весов в группах по МНК находят как: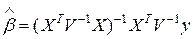 
;
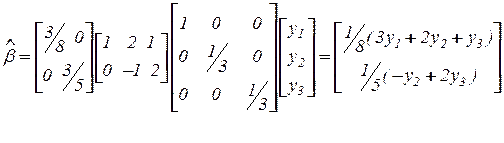
Теперь сравним дисперсии оценок средних весов предметов в группах по МНК и обычным способом с отдельным взвешиванием каждого предмета, если значение дисперсии каждого измерения -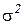 
.
По МНК дисперсионная матрица оценок 
равна: 
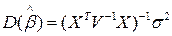т.е.
- дисперсия оценки среднего веса 1 группы предметов,
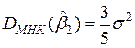- дисперсия оценки среднего веса предметов 2 группы.
Примерно того же результата можно достичь, выполняя измерения обычным способом, если взвесить по 2 предмета каждой группы и найти среднее в каждой из групп, т.е. выполнить 4 измерения вместо 3, как в рассмотренной выше процедуре взвешивания.
Для некоррелированных случайных величин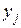 
: 
.
; 
;
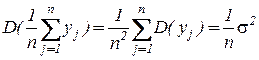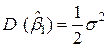Такое превышение числа испытаний может оказаться значительным при дорогостоящих исследованиях. При числе испытаний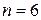 
и симметричном относительно взвешиваемых предметов эксперименте 
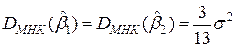, тогда как при раздельном взвешивании предметов 
; СКО оценок соответственно равны: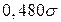 
и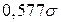 
.
|
|
|
Проверим гипотезу о равенстве средних весов в обеих группах предметов:
: 
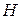- средние веса этих двух групп предметов равны между собой.
, 
,
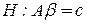
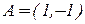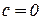
Выпишем - статистику (3.5) для неравноточных наблюдений; (обобщенный МНК):
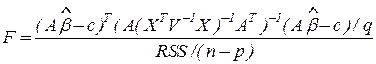3.9
здесь - произведено 3 измерения,
- количество строк в матрице ограничений 
,
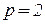- два параметра в модели данных МНК 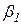и .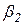
Вычислим отдельные сомножители в (3.9):
;
;
;
.
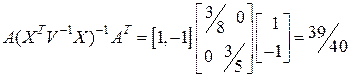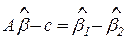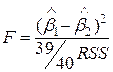Проверим справедливость гипотезы 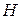сравнением с границей критической области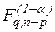 
, при уровне значимости критерия - 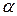. Уровень значимости критерия 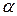обычно выбирают из стандартного набора чисел 0.1, 0.05, 0.01, 0.005. При 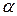=0.05, 
, квантиль уровня 0.95 распределения Фишера равен 
. Если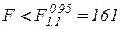 
, гипотеза о равенстве средних весов двух групп предметов принимается.
Рассмотренную процедуру взвешивания можно применить и для поверки самих весов, используя эталонные гири; при этом ошибки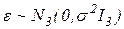 
|
|
|
