 |
Кусочно-полиномиальная аппроксимация.
|
|
|
|
Иногда полиномиальная аппроксимация оказывается неудовлетворительной даже при использовании ортогональных полиномов вплоть до порядка двадцатой степени. Несогласованность таблицы наблюдений и аппроксимирующих полиномов обнаруживается по отсутствию стабилизации RSS.
Несмотря на то, что с увеличением порядка полинома 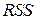 уменьшается (не возрастает); график остатков может иметь тенденции роста или убывания с изменением
уменьшается (не возрастает); график остатков может иметь тенденции роста или убывания с изменением 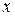 , между соседними точками
, между соседними точками  , по которым подбиралась кривая, могут наблюдаться осцилляции.
, по которым подбиралась кривая, могут наблюдаться осцилляции.
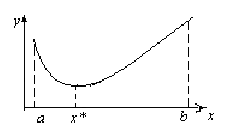
Такие трудности возникают, как правило, в тех случаях, когда поведение изучаемой функции оказывается существенно различным на разных частях отрезка наблюдений. Например, функция может быстро изменяться в одной области и медленно – в другой.
Одним из приемов действий в таких случаях является деление всего отрезка значений 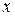 на более мелкие отрезки и подбора на каждом из них разных кривых. Затем подобранные кривые «сшиваются» так, чтобы обеспечить «гладкое» сопряжение отдельных кусков.
на более мелкие отрезки и подбора на каждом из них разных кривых. Затем подобранные кривые «сшиваются» так, чтобы обеспечить «гладкое» сопряжение отдельных кусков.
Рассмотрим случай, когда область изменения переменной 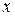
 делится на два интервала
делится на два интервала  и
и  . На каждом из этих интервалов раздельно выполняется подгонка таблицы наблюдений полиномами. Пусть на первом интервале
. На каждом из этих интервалов раздельно выполняется подгонка таблицы наблюдений полиномами. Пусть на первом интервале  - таблица наблюдений хорошо аппроксимируется полиномом
- таблица наблюдений хорошо аппроксимируется полиномом 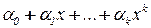 , а на втором
, а на втором  - полиномом
- полиномом  .
.
Обозначим  наблюдения
наблюдения  на первом интервале
на первом интервале  , соответственно
, соответственно  - наблюдения на интервале
- наблюдения на интервале 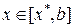 . Тогда раздельная подгонка таблицы наблюдений на первом и втором интервале выполняется решением двух задач МНК:
. Тогда раздельная подгонка таблицы наблюдений на первом и втором интервале выполняется решением двух задач МНК:
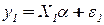
 .
.
Здесь 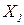 и
и 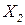 - матрицы плана соответствующие виду полинома и точкам наблюдений на отрезках
- матрицы плана соответствующие виду полинома и точкам наблюдений на отрезках  и
и  .
.
Эти две задачи можно записать как одну, сформировав общую матрицу плана  ,
,
|
|
|
 .
.
Теперь о том как «сшиваются» отдельные куски подогнанной кривой. Для «сшивания» используется правило построения МНК оценок при наличии линейных ограничений [см. _ ].
Если в задаче  наложены линейные ограничения на значения параметров
наложены линейные ограничения на значения параметров  вида
вида  , то оценка параметров
, то оценка параметров  при ограничениях
при ограничениях 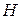 вычисляется как:
вычисляется как:
 ,
,
где  - МНК оценка параметров
- МНК оценка параметров  без всяких ограничений на параметры.
без всяких ограничений на параметры.
Стандартные условия «гладкого» перехода одной кривой  в другую
в другую  является совпадение кривых в точках сопряжения (у нас это одна точка
является совпадение кривых в точках сопряжения (у нас это одна точка 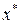 ) по значению и по производным (обычно по первой производной, иногда по первой и по второй производной).
) по значению и по производным (обычно по первой производной, иногда по первой и по второй производной).
Запишем условие совпадения кривых  и
и  по значению в точке
по значению в точке 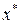
 или в матричном виде:
или в матричном виде:
 ; где
; где  ;
; 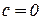
Если требуется еще и гладкое сопряжение кривых по первой производной, в матрицу  добавляется еще одна строка:
добавляется еще одна строка:
 .
.
Замечание 1. Каждое ограничение «гладкости» сопряжения кусков кривых уменьшает на единицу общее число параметров, используемых для приближения таблицы наблюдений.
Не всегда положение точки 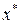 , разделяющей область
, разделяющей область  изменения
изменения 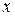 известно заранее. В этом случае положение точки
известно заранее. В этом случае положение точки 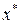 подбирают, используя метод проб и ошибок. Решают серию задач с варьированием положения точки
подбирают, используя метод проб и ошибок. Решают серию задач с варьированием положения точки 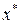 , и выбирают то значение, при котором
, и выбирают то значение, при котором 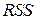 задачи
задачи
 ; принимает минимальное значение.
; принимает минимальное значение.
Замечание 2. Приведенная процедура кусочно - полиномиального приближения таблиц наблюдений используется при построении МНК-сплайнов  порядка
порядка  . Узлами сплайнов являются точки
. Узлами сплайнов являются точки 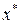 , разделяющие область
, разделяющие область  на подинтервалы; на каждом подинтервале по таблице наблюдений подбирается полином порядка не выше
на подинтервалы; на каждом подинтервале по таблице наблюдений подбирается полином порядка не выше  . Подобранные полиномы сшиваются в точках сопряжения интервалов. Обычно кубический сплайн
. Подобранные полиномы сшиваются в точках сопряжения интервалов. Обычно кубический сплайн  порядка
порядка 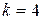 вполне удовлетворителен для подбора, а свойство непрерывности значений подбираемой кривой и ее производных до 2-го порядка достаточно для большинства практических задач.
вполне удовлетворителен для подбора, а свойство непрерывности значений подбираемой кривой и ее производных до 2-го порядка достаточно для большинства практических задач.
|
|
|
|
|
|


