 |
Применение сингулярного разложения в задаче построения линейной регрессии.
|
|
|
|
Пусть в задаче подбора регрессионной зависимости 
матрица 
имеет размерность 
и 
.
Запишем сингулярное разложение матрицы : 
при 
; 
:
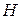- ортогональная матрица размера (
),
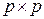- ортогональная матрица размера (
),
– диагональная матрица размера (),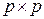 
- сингулярные числа 
.
Воспользуемся теоремой Лоусона-Хенсона, чтобы ослабить эффекты плохой обусловленности матрицы 
при решении задачи подбора зависимости 
.
В задаче при 
запишем:
и вычислим вектор 
, 
;
; 
компоненты 
нет;
; 
.
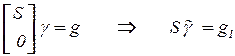Матрица диагональная, поэтому каждый элемент решения 
есть: 
.
Так как сингулярные числа располагаются по не возрастанию, компоненты решения с большими номерами находятся делением на малые сингулярные числа и могут иметь большие значения (малым сингулярным числам соответствуют малые собственные числа матрицы ).
Посмотрим, что произойдет, если мы удалим самые малые сингулярные числа и перейдем к задаче, в которой в матрице нижние строки (или строка) заменяются нулями.
При этом мы переходим от решения МНК задачи подбора зависимости , где к задаче 
, в которой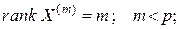 
однако матрицы плана 
и близки, поскольку матрица получена заменой в разложении малых сингулярных чисел нулями:
Элементы решения 
системы 
задачи 
равны 
первым элементам вектора 
(вычисляются по одним и тем же формулам (6.10)); соответствующий вектор минимальной длины размера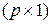 
есть: 
,
вектор решения задачи есть: 
;
квадрат его нормы: 
,
так как и - ортогональная матрица.
Следовательно, норма 
– неубывающая функция (длина вектора 
тем больше, чем больше в нем ненулевых элементов).
Квадрат нормы невязки, отвечающий вектору равен:
6.11
- невозрастающая функция m (если уменьшить число оставляемых элементов вектора 
, то увеличивается).
|
|
|
Естественно 
(
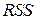исходной МНК задачи).
Предположим, что матрица плохо обусловлена. Тогда некоторые из сингулярных чисел с большими номерами будут существенно меньше предшествующих.
В этом случае решения 
, отвечающие строкам с малыми 
могут быть слишком велики.
В типичной ситуации заменяют малые нулями и пытаются найти такой индекс , чтобы:
- все элементы решения 
, 
были достаточно малы и не сильно отличались друг от друга,
- все сингулярные числа достаточно велики,
- а норма невязки (6.11), отвечающая укороченному вектору решений, достаточно мала, т.е. 
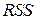и - не сильно различались между собой.
Итак, использование сингулярного разложения при решении задачи подбора зависимости y @ X·b по таблице наблюдений позволило:
1. формализовать процедуру выявления линейной связи между столбцами матрицы ;
после замены в матрице малых сингулярных чисел 
нулями:
матрица 
имеет ранг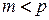 
;
и вместо ‘сильной линейной’ связи столбцов в преобразованной матрице 
столбцы строго линейно зависимы и существует (
) уравнений линейной связи;
операция приравнивания () малых сингулярных чисел нулю эквивалентна введению такого же количества явных линейных связей между регрессорами.
2. указать правила выбора независимых регрессоров на основе числа обусловленности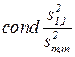 
;
3. найти решение минимальной длины 
задачи , при котором норма остатков не сильно отличается от нормы остатков решений исходной задачи.
4. уменьшить полную среднеквадратическую ошибку вектора по сравнению с 
.
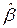Робастное оценивание
Робастным называют оценивание, устойчивое к возможным неверным предположениям о характере ошибок наблюдений и грубым промахам в наблюдениях.
Грубые промахи (грубые ошибки, выбросы) в обрабатываемых данных встречаются довольно часто. Это может быть следствием не замеченных вовремя ошибок в измерительном тракте (сбои и отказы измерительных преобразователей, ошибки операторов). Бывают случаи, когда в обрабатываемый массив попадают и вовсе посторонние данные.
|
|
|
При ручном счете профессиональный статистик способен обнаружить и скорректировать подобные ошибки, однако автоматические компьютерные системы сбора, обработки и идентификации данных могут выдать абсолютно неверные результаты, если не принять специальных мер в процессе выработки решений.
Загрязнение наблюдений выбросами приводит к тому, что основные предположения МНК нарушаются и ожидать хороших приближений, используя обычный МНК, не приходится.
При наличии выбросов в данных следует отказаться от предположения о нормальном распределении ошибок наблюдений в пользу так называемых распределений с «тяжелыми хвостами».
Для случайных величин, имеющих распределения с «тяжелыми хвостами» характерна высокая вероятность появления реализаций в областях, далеко расположенных от центра распределения.
Нормальное распределение имеет «легкие хвосты».
Вне интервала (-3s, 3s) находится всего лишь 0,27% распределения
Среди распределений с «тяжелыми хвостами» можно указать:
1. Распределение Тьюки:
, 7.1
где e - малая доля наблюдений с большой дисперсией или, другими словами, доля загрязнения основной выборки.
2. Распределение Коши
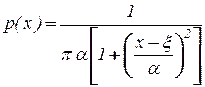, 7.2
где x - центр распределения,
a - характеристика рассеяния (масштаба).
Отметим, что это распределение не имеет моментов.
Итак, при наличии выбросов в наблюдениях:
1. нарушаются основные предположения МНК о распределениях ошибок: 
следствие этого – возможная смещенность и неэффективность оценок;
2. выводы теории МНК, основанные на нормальности ошибок (проверка гипотез, построение доверительных интервалов и т.д.), оказываются сомнительными.
Посмотрим, как влияют выбросы на результаты оценивания. Начнем с простейшей задачи определения «положения» выборочных данных. Обычно для таких целей используют выборочное среднее 
, которое является МНК-оценкой для 
. Однако, возможна и другая оценка положения – выборочная медиана: 
.
В случае, когда все 
имеют нормальное распределение 
|
|
|
выборочное среднее 
имеет распределение 
,
а выборочная медиана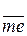 
- 
.
Сравнение дисперсий этих оценок показывает, что 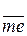менее эффективна, чем :
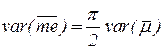
При наличии выбросов в выборке эффективность оценок меняется.
Рассмотрим пример:
выборка 
представлена следующим набором значений:
{1.1, 0.9, 0.8, 1.2, 1.0}
В этом случае: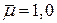 
, 
Теперь предположим, что последнее значение массива введено с ошибкой: вместо значения 1.0 в расчетах используется 10 (при вводе числа 1.0 пропустили точку).
Для такого массива 
, 
.
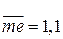Оценка 
оказалась сильно зависимой от «выброса», тогда как 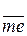практически осталась без изменений.
Итак, выборочная медиана устойчива к выбросу, а выборочное среднее нет.
Еще более чувствительна к выбросам оценка рассеяния (масштаба, стандартного отклонения):
Сравним эту оценку с другой оценкой рассеяния – средним абсолютным отклонением:
Известно, что 
– наилучшая оценка рассеяния для нормальных выборок, но стоит выбросам появиться в выборке, как эти преимущества теряются.
Дж.Тьюки исследовал влияние степени засорения выборки на качество оценок и 
. Засорение нормальной выборки 
осуществлялось заменой 
- доли отсчетов на отсчеты из 
(См. распределение (7.1))
Сравнение качества оценок проводилось на основе критерия
АОЭ – ассимптотической относительной эффективности:
| e | АОЭ |
| 0 | 0,876 |
| 0,001 | 0,948 |
| 0,002 | 1,016 |
| 0,05 | 2,035 |
Результаты исследо-
ваний приведены в
таблице:
При отсутствии засорения (e=0) оценка примерно на 12% лучше оценки по критерию АОЭ. При доле засорения =0,002 (два чужих отсчета или две засоренные точки на тысячу), оценки и практически одинаковы.
При засорении e=0,05 оценка вдвое хуже .
Для количественной характеристики способности оценки противостоять действию выбросов вводят понятие пороговой точки.
Пороговой точкой оценки называют ту долю выбросов в выборке, начиная с которой выбросы оказывают катастрофическое влияние на результаты оценивания.
Так, для выборочной медианы - оценке положения данных пороговая точка равна 0,5, т.е., если в выборке окажется менее половины наблюдений с грубыми ошибками, это не приведет к серьезным отклонениям в значениях оценки.
|
|
|
Для выборочного среднего пороговая точка равна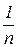 
; и наличие всего одного выброса может привести к непредсказуемым смещениям оценки положения.
Поэтому из этих двух оценок положения (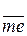 и ), первая обладает исключительно малой чувствительностью к выбросам (устойчива к выбросам) и в то же время, при отсутствии грубых искажений выборка 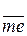(величина стандартного отклонения примерно на 20% больше чем ) оказывается менее эффективной, чем .
Это повлекло за собой попытку создания оценок, совмещающих в себе высокую устойчивость и высокую эффективность.
Такими оценками положения являются, например:
1. 
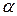- цензурированная оценка положения
в упорядоченной по возрастанию выборке 
:
удаляется 
«наибольших» и «наименьших» наблюдений и по оставшимся наблюдениям вычисляют:
. 
2. 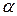- винзорированная оценка положения.
В упорядоченной по возрастанию выборке 
указывают «наибольших» и «наименьших» элементов и заменяют их ближайшими к ним внутренними элементами упорядоченной выборки;
пусть для примера 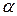и 
таковы, что в выборке это 
и 
, тогда
формируют новую выборку 
объема n, в которой заменяются на 
, а на 
и по полученной выборке:
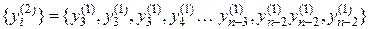
вычисляют 
Пороговая точка таких оценок равна 
, а эффективность несколько выше, чем у выборочной медианы.
Примером оценки рассеяния (масштаба) выборки с пороговой точкой, равной 0,5 может быть МАО (медиана абсолютных отклоненийот медианы):
Для нормально распределенных наблюдений E{MAO}=0,6345 
. Эффективность МАО как оценки достигает 87%.
|
|
|
