 |
Устойчивые методы оценивания параметров регрессионной модели.
|
|
|
|
Оценки параметров 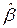 регрессионной модели
регрессионной модели 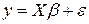 по МНК находят, минимизируя по
по МНК находят, минимизируя по  функционал:
функционал:  ;
;
т.е.  7.3
7.3
здесь 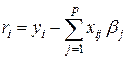 - остатки подгонки по МНК.
- остатки подгонки по МНК.
Если в наборе данных  имеются выбросы, МНК -оценки
имеются выбросы, МНК -оценки 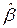 могут существенно смещаться (квадраты больших уклонений в формуле (7.3) заметно сдвигают
могут существенно смещаться (квадраты больших уклонений в формуле (7.3) заметно сдвигают 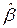 от истинного
от истинного  ).
).
Нас никто не заставлял выбирать именно критерий (7.3), можно перейти к другим критериям, в которых зависимость оценок 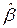 от отклонений в отдельных точках менее слабая, чем квадратичная.
от отклонений в отдельных точках менее слабая, чем квадратичная.
Например, можно перейти к критерию:
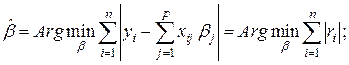 7.4
7.4
Оценки 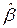 по критерию (7.4) носят название оценок по методу наименьшихмодулей (МНМ -оценки).
по критерию (7.4) носят название оценок по методу наименьшихмодулей (МНМ -оценки).
Можно построить оценки на основе минимизации по  суммы функций
суммы функций 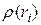 отклонений:
отклонений:
 7.5
7.5
Эти оценки 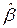 носят название М -оценок.
носят название М -оценок.
Функция 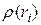 остатков должна быть такой, чтобы малые по модулю остатки оказывали влияние на результаты подгонки, а очень большие – нет. Кроме того, желательна дифференцируемость функций
остатков должна быть такой, чтобы малые по модулю остатки оказывали влияние на результаты подгонки, а очень большие – нет. Кроме того, желательна дифференцируемость функций  . В этом случае задача отыскания оценок сводится к решению системы
. В этом случае задача отыскания оценок сводится к решению системы  нелинейных уравнений:
нелинейных уравнений:
 .
.
Здесь  производные функции
производные функции 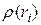 по
по  .
.
Итак, желательно, чтобы функция  имела примерно следующий вид:
имела примерно следующий вид:

В области 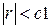 зависимость примерно квадратичная.
зависимость примерно квадратичная.
В области  зависимость примерно линейная.
зависимость примерно линейная.
При 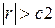 - слабо растущая функция r.
- слабо растущая функция r.
Вид функции  определяет тип М -оценки, которые связывают с именами авторов.
определяет тип М -оценки, которые связывают с именами авторов.
Еще один класс устойчивых оценок параметров модели 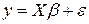 строится на основе упорядоченных соотношений между остатками
строится на основе упорядоченных соотношений между остатками 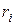 и соответствующими им наблюдениями
и соответствующими им наблюдениями 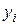 . Этот класс известен как L -оценки.
. Этот класс известен как L -оценки.
При построении L -оценок остатки  упорядочиваются по возрастанию (
упорядочиваются по возрастанию (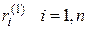 - вариационный ряд), так, что наибольшие по модулю уклонения оказываются на краях ряда
- вариационный ряд), так, что наибольшие по модулю уклонения оказываются на краях ряда  . В минимизируемом по
. В минимизируемом по  функционале, этим значениям остатков присваивают малые веса по сравнению со средними членами:
функционале, этим значениям остатков присваивают малые веса по сравнению со средними членами:
|
|
|

Вид функции  определяет тип L -оценки.
определяет тип L -оценки.
Введенные выше устойчивые оценки параметров регрессионной модели являются нелинейными функциями наблюдений.
Так, что при наличии выбросов в наблюдениях оценки параметров регрессионной модели строят в классе нелинейных оценок.
Точки разбалансировки.
Вернемся к задачам подгонки модели по методу наименьших квадратов. Мы уже видели, что расположение точек, в которых проводятся наблюдения, существенно влияет на качество подгонки.
Рассмотрим влияние отдельных точек на результаты приближения таблицы наблюдений. Начнем с примера.
На рисунке представлено расположение наблюдений, по которым предполагается построить линейную зависимость. Наблюдения можно разделить на две группы: одна – компактно расположенные 5 наблюдений в левой части рисунка, другая – единственная точка, расположенная далеко вправо от первой группы.

Точка  оказывает существенно большее влияние на результаты подгонки, чем все остальные. На рисунке прямая - 1 проведена по всем шести точкам. Прямая - 2 соответствует подгонке по 5 - ти точкам с удалением точки
оказывает существенно большее влияние на результаты подгонки, чем все остальные. На рисунке прямая - 1 проведена по всем шести точкам. Прямая - 2 соответствует подгонке по 5 - ти точкам с удалением точки  из массива обрабатываемых данных.
из массива обрабатываемых данных.
Эффект удаления всего одной точки из таблицы наблюдений поразительный: остаточная сумма квадратов 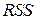 для подгонки 2 значительно меньше, чем для прямой 1.
для подгонки 2 значительно меньше, чем для прямой 1.
Как относиться к точке  ? Если это выброс, то подгонка 2 – удачное решение. Если у нас нет оснований считать точку
? Если это выброс, то подгонка 2 – удачное решение. Если у нас нет оснований считать точку  выбросом, то можно попытаться улучшить подгонку, выбрав другую модель для таблицы наблюдений. Кривая 3 соответствует модели
выбросом, то можно попытаться улучшить подгонку, выбрав другую модель для таблицы наблюдений. Кривая 3 соответствует модели
y = b0 + b1x + b2x2.
Проблема выбора наилучшей модели связи между переменными окончательно может быть решена только после проведения дополнительных исследований по выявлению причин сильного отклонения точки  от прямой 2,
от прямой 2,
|
|
|
Итак, существуют точки, которые могут оказывать сильное влияние на результаты подгонки. Их называют точками разбалансировки (англ. leverages –рычаги).
Как их обнаружить, чтобы до начала вычислений иметь представление о степени влияния каждой из точек?
При оценивании по МНК 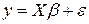 ;
;  ;
; 
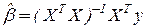

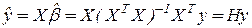
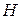 - матрица подгонки;
- матрица подгонки;  ;
;  ;
;  ;.
;.
Вычислим дисперсию оценки регрессии 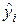 в опорной точке
в опорной точке  (где
(где 
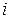 -ая строка матрицы плана Х) двумя способами.
-ая строка матрицы плана Х) двумя способами.
Способ 1

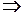

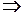
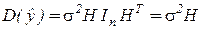
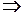
 . Способ 2
. Способ 2

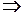


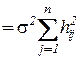 .
.
Сравнивая полученные результаты, получаем: 
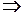
 все
все  .
.
 – коэффициент, указывающий на влияние наблюдений
– коэффициент, указывающий на влияние наблюдений  на оценку
на оценку  в точке
в точке  .
.
Итак, если  будет близок к 1, то в этом случае влияние остальных данных на оценку в точке
будет близок к 1, то в этом случае влияние остальных данных на оценку в точке  будет ничтожным.
будет ничтожным.
Определение. Точки плана Х, которым соответствуют большие диагональные элементы  матрицы проектирования H, называют точками разбалансировки.
матрицы проектирования H, называют точками разбалансировки.
Остатки и выделяющиеся значения (выбросы).
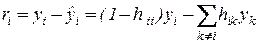
Итак, если  велико (близко к 1), то большая ошибка (выброс в
велико (близко к 1), то большая ошибка (выброс в 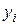 ) не обязательно проявится в i-ом остатке.
) не обязательно проявится в i-ом остатке.
Планы, в которых  <0,2 достаточно надежны. Если
<0,2 достаточно надежны. Если  >0,5, то лучше избегать использования этих точек в оценках.
>0,5, то лучше избегать использования этих точек в оценках.
Хампель уточняет рассмотренную ситуацию и предлагает обращать особое внимание на точки, в которых  >2
>2 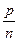 , где
, где  – ранг матрицы Х.
– ранг матрицы Х.
Теорема 1. Если ошибки наблюдений независимы, имеют нулевое среднее и одинаковую дисперсию  , то значение
, то значение 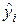 состоятельно тогда и только тогда, когда
состоятельно тогда и только тогда, когда  при
при 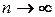 , а все подогнанные значения
, а все подогнанные значения 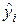 состоятельны тогда и только тогда, когда
состоятельны тогда и только тогда, когда  при
при 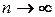 .
.
При выполнении этих условий справедливо:

 ;
;

 для всех
для всех 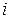 и
и 
 ;
;  .
.
Для состоятельности оценок по МНК, необходимо, чтобы планы Х были сбалансированными, т.е. не содержали точек со значениями  , не убывающими с увеличением общего числа наблюдений n.
, не убывающими с увеличением общего числа наблюдений n.
Оказывается, что сбалансированность планов гарантирует «нормальность» оценок даже в том случае, когда распределения ошибок  в модели
в модели 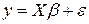 отличаются от нормальных.
отличаются от нормальных.
Теорема 2. МНК-оценка  произвольной линейной комбинации
произвольной линейной комбинации  асимптотически нормальна при произвольном распределении ошибок
асимптотически нормальна при произвольном распределении ошибок  с
с
атрицы проектирования мых данных.сем шести точкам. Прямая 2 соответствует подгонке пот 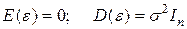 , если:
, если:
 ,
,  =const; i=1,n;
=const; i=1,n;  ,
,
где 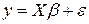 , Х – матрица размера
, Х – матрица размера  и ранга;
и ранга;  .
.
Пусть  (столбцы матрицы Х ортонормированы) и
(столбцы матрицы Х ортонормированы) и
аТа=1 ( -имеет единичную длину),
-имеет единичную длину),
|
|
|
тогда:
 т.к.
т.к.  ;
;
 - линейная комбинация наблюдений;
- линейная комбинация наблюдений;
 ; длина вектора
; длина вектора  при любом
при любом  одинакова и равна 1, а
одинакова и равна 1, а  постоянна (при любом
постоянна (при любом  величина
величина  не содержит слагаемых, имеющих дисперсию больше
не содержит слагаемых, имеющих дисперсию больше 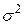 ).
).
Для того чтобы в соответствии с “центральной предельной теоремой” сумма многих случайных величин имела асимптотически нормальное распределение, масштаб рассеяния слагаемых должен быть ограничен. Это обеспечивается условием  ,
,
Требования асимптотической нормальности сводятся к равномерному стремлению к нулю при n→∞ всех компонент вектора  (
( -вектор влияния наблюдений на оценку
-вектор влияния наблюдений на оценку  ; s аналогичен строке матрицы H;
; s аналогичен строке матрицы H;  ).
).
При выполнении условий теоремы 2 асимптотически нормальными являются МНК-оценки параметров регрессий, оценки регрессий, прогнозы и т.д.
Замечания.
Если  велико, то его можно уменьшать, увеличив количество наблюдений в точке
велико, то его можно уменьшать, увеличив количество наблюдений в точке  (на самом деле производят приблизительное дублирование, т.е. наблюдения при слегка измененных условиях, чтобы избежать повторения возможных систематических ошибок). Это так называемая рандомизированная процедура проведения эксперимента.
(на самом деле производят приблизительное дублирование, т.е. наблюдения при слегка измененных условиях, чтобы избежать повторения возможных систематических ошибок). Это так называемая рандомизированная процедура проведения эксперимента.
Если исследователь имеет возможность активно планировать эксперименты по сбору данных, следует выбирать сбалансированные планы.
|
|
|


