 |
Итерационный взвешенный метод наименьших квадратов (ИВМНК).
|
|
|
|
ИВМНК используют для уменьшения влияния возможных выбросов в данных. В основу метода положена ранее рассмотренная идея построения устойчивых оценок (оценок с высокой пороговой точкой). При вычислении таких оценок наблюдениям, сильно отличающимся по величине от остальных, присваивались малые или даже нулевые веса.
Процедура ИВМНК начинается с построения ВМНК-оценок по всем данным с одинаковыми весами: 
. На очередной k -ой итерации веса назначаются в зависимости от величины остатков 
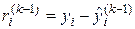подгонки на предыдущей итерации.
Наблюдениям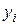 
, соответствующим большим остаткам 
присваивают заниженные веса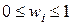 
.
При построении взвешенных МНК-оценок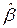 
влияние наблюдения 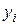ослаблено весовым коэффициентом 
, если 
и исключено полностью, если 
.
Известны несколько правил выбора 
. Рассмотрим процедуру Тьюки назначения весов на очередном шаге ИВМНК.
,
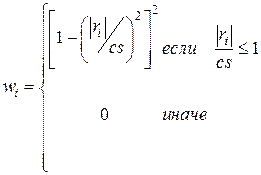При остатке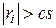 
наблюдение 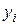считается выбросом, а вес назначается равным нулю.
Кривая биквадратного взвешивания остатков.
Алгоритм построения ИВМНК-оценок.
 |
Обычно бывает достаточно 3-5 итераций для окончания процесса подгонки.
Рассматривая проблему точек разбалансировки, мы видели, что в точках разбалансировки (там, где 
близко к 1) выброс в наблюдениях не обязательно приводит к большим остаткам. Так что выброс в точке разбалансировки не обнаруживается приведенным выше алгоритмом. Чтобы исключить такую ситуацию, можно модифицировать процедуру выбора весов
,
ослабив или исключив влияние данных в точке разбалансировки.
Можно рассмотреть несколько более сложную процедуру выбора весов, в которой влияние i -го наблюдения снижается при одновременном выполнении двух условий (наличие большого остатка и наблюдение в точке разбалансировки при >0,5).
|
|
|
По окончании подгонки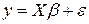 
по ИВМНК обязательно должен составляться протокол о всех наблюдениях, взятых на последней итерации с малыми весами для дальнейшего выявления причин, вызвавших такой эффект.
Данные, которые трактуются нами как выбросы, могут иметь значительно большую ценность, чем все остальные.
8. Следствия нарушения основных предположений МНК.
В МНК подбирается зависимость переменной у от регрессоров (факторов) 
; 
; на основе n - наблюдений переменной 
при фиксированных значениях регрессоров.
Основные предположения МНК: 8.1
- модель данных есть 
,
- значения регрессоров в каждом из наблюдений задаются точно,
- ошибки 
наблюдений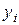 
являются случайными и имеют одинаковые распределения,
- 
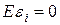, ошибки не смещены,
- 
, ошибки не коррелированны,
- распределение ошибок нормально.
Однако отклонения от этих предположений при расчетах может привести к ошибкам. Например, вследствие того, что в модель включено недостаточное или избыточное количество регрессоров. Рассмотрим эффекты отклонений от указанных предположений.
Неполнота моделей.
Пусть существующая связь между наблюдениями и регрессорами описывается соотношением: 
. 8.2
Однако по ряду причин при подборе зависимости в модель данных мы включили не все регрессоры,
а только часть их: 8.3
и не ведая о существовании других регрессоров, подобрали вектор параметров:
Математическое ожидание оценки 
есть:
= 
8.4
В результате оценка оказывается смещенной на величину 
. Решая МНК-задачу (8.3) вместо задачи (8.2) мы находим связь y только с частью регрессоров, влияющих на y, да и ту с систематическими ошибками. Однако возможна ситуация, когда 
, при этом векторы значений регрессоров обеих групп в точках наблюдений оказываются взаимно ортогональными. В этой случае смещение оценок отсутствует.
|
|
|
Оценка 
для 
, вычисляемая по неполной модели данных (8.3), смещена:
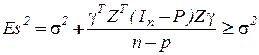; здесь n - количество наблюдений переменной y,
p - число учитываемых регрессоров,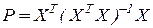 
- матрица проектирования и X - матрица плана размера 
в МНК-задаче (8.3),
Z - матрица значений неучтенных регрессоров и 
- вектор неучтенных параметров.
Построение прогнозов переменной y в точку 
; Поскольку оценки смещены, то и прогнозы смещены.
Остатки
. Остатки смещены.
|
|
|
