 |
Диагностика регрессионной модели.
|
|
|
|
Качество подгонки данных к модели 
определяют по остаткам 
, 
.
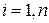В векторном виде:
,
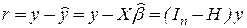
где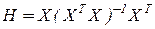 
- матрица подгонки.
Если регрессия подобрана правильно, остатки 
представляют собой последовательность независимых случайных величин.
Свойства остатков.
Если в регрессионной зависимости есть регрессор «1», т.е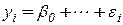 
, то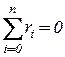 
.
Если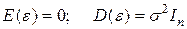 
, то 
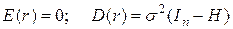8.15
Кроме того,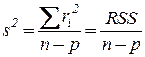 
- несмещенная оценка 
.
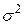Из (8.15) следует, что ковариационная матрица векторов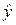 
и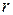 
равна:
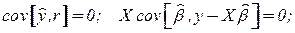
Действительно:
; 
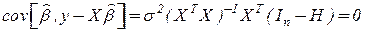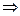
Рассмотрим теперь некоторые графические методы, основанные на остатках и дающие возможность исследовать отклонения от основной модели и от сделанных предположений относительно распределений.
Всякое отклонение от сделанных предположений относительно распределения e отражаются на векторе r. По виду графиков можно судить о характере отклонений.
Графики остатков.
Первый шаг при построении графиков состоит в выборе такого масштаба остатков, при котором они будут иметь дисперсии приблизительно равные.
Средняя дисперсия остатков
.
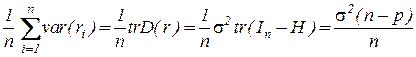здесь 
– количество регрессоров в модели, n – число наблюдений.
От остатков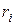 
можно перейти к шкалированным остаткам:
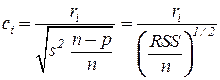, 8.16
где 
– оценка для 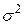, равная: 
,
(шкалированние - стандартизация остатков на основе средней дисперсии),
или к стьюдентизированным остаткам:
8.17
(стьюдентизизация - стандартизация остатков на основе дисперсии каждого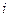 
- го остатка).
Хотя сами остатки ri и их стандартизованные варианты (формулы (8.16) и (8.17)) коррелированы между собой: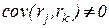 
, но эта корреляция мало влияет на характер графиков и мы можем обращаться с величинами 
как с независимыми одинаково распределенными величинами N(0,1).
Во многих случаях в формуле (8.17) можно пренебречь малыми величинами 
и вычислять 
.
|
|
|
Использование шкалированных и стьюдентизированных остатков позволяет обнаруживать выбросы: Если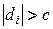 
|, то в точке 
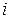выброс,
здесь с – пороговая константа.
Например, при с=3 остаток 
, выходящий за 3s зону, можно считать выбросом в точке .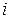
а) Графики остатков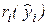 
.
ri
| |||||||
 | |||||||
 | |||||||
 | |||||||
 | | ||||||
 | |||||||
|
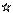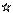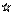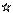б) Прогрессирующее изменение разброса остатков с увеличением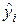 
либо времени дает основание считать, что предположение о равенстве дисперсий не оправдано и следует уточнить модель ошибок наблюдений; применение ВИМНК может автоматически устранить влияние изменчивости дисперсии.
в) Наличие заметного тренда на графиках остатков возникает в случае, когда неверно выбрана модель (модель неадекватна данным). Если какой-либо фактор был пропущен в модели, то это может быть выявлено по графику зависимости остатков от этого фактора (конечно, если уровни пропущенного фактора известны для каждого остатка).
Например, если пропущенный фактор время (обычно номер наблюдения связан со временем), то время как пропущенный фактор можно учесть, введя дополнительную зависимость отклика от номера наблюдения. В связи с этим полезно помимо графиков 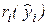строить и зависимости 
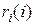, где 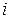- номер наблюдения и проверять наличие корреляции между остатками в ряду .
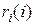Тест на независимость последовательности остатков.
Если отсчета выполнены с равными интервалами по времени, то наиболее мощным критерием наличия корреляции внутри ряда является критерий Дарбина-Уотсона:
.
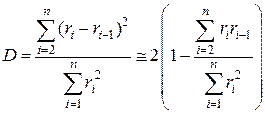Если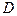 
близко к нулю имеет место сильная положительная корреляция, при 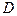близком к четырем – сильная отрицательная корреляция, при 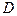=2 - отсутствие корреляции.
|
|
|
Критерий табулирован. Существуют таблицы для проверки нулевой гипотезы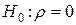 
против альтернативы 
и т.д.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК.
1. Себер Дж. Линейный регрессионный анализ. – М.: Мир, 1980. – 456с.
2. Демиденко Е.З. Линейная и нелинейная регрессия / Демиденко Е.З. – М.: “Финансы и Статистика”,1981. – 302с.
3. Бояджиева Л., Прикладной линейный регрессионный анализ. / Вучков И., Бояджиева Л., Солаков Е. – М.: “Финансы и Статистика”,1987. – 238с.
4. Хампель Ф. Робастность в статистике / Хампель Ф., Рончетти Э., Рауссеу П., Штаель В. – М.: Мир, 1989.–512 с.
5. Хьюбер Дж. Робастность в статистике / Хьюбер Дж. – М.: Мир, 1984.–304 с.
6. Дрейпер Н., Прикладной регрессионный анализ / Дрейпер Н., Смит Г – М.: Статистика, 1966.–304 с.
7. Мостеллер Ф., Анализ данных и регрессия / Мостеллер Ф.,Тьюки Дж. – М.: Финансы и статистика, 1988. Вып.1 и 2 – 684с.
8. Дидэ Э. Методы анализа данных. – М.: Финансы и статистика, 1988.– 406с.
9. Лоусон Ч.,, Численное решение задач метода наименьших квадратов / Лоусон Ч., Хенсон Р. – М.: Наука, 1986.– 184с.
10. Андерсон Т. Статистический анализ временных рядов. – М.: Мир, 1976.– 755с.
11. Мэйндональд Дж. Вычислительные алгоритмы в прикладной статистике. – М.: Финансы и статистика, 1988.– 350с.
12. Линник Ю.В. Метод наименьших квадратов и основы обработки наблюдений. – М.: Физматгиз, 1962. – 355с.
|
|
|
