 |
Комментарий. Задача 12 (демонстрационный вариант 2022 г.). б) Укажите корни этого уравнения, принадлежащие отрезку. Задание 1
|
|
|
|
Комментарий
Ответ в задании с развёрнутым ответом – это решение и вывод (называемый ответом).
Задача 12 (демонстрационный вариант 2022 г. )
а) Решите уравнение
 .
.
б) Укажите корни этого уравнения, принадлежащие отрезку  .
.
Решение.
а) Запишем исходное уравнение в виде:
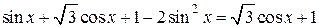 ;
;  ;
; 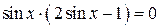 .
.
Значит, 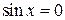 , откуда
, откуда 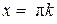 ,
, 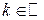 , или
, или  , откуда
, откуда 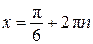 ,
, 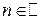 , или
, или  ,
,  .
.
|
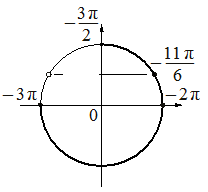
б) С помощью числовой окружности отберём корни, принадлежащие отрезку  .
.
Получим числа: 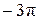 ;
; 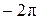 ;
; 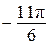 .
.
Ответ: а) 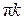 ,
, 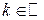 ;
;  ,
, 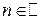 ;
;
Ответ:  ,
,  ;
;
Ответ: б) 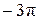 ;
; 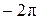 ;
; 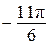 .
.
Комментарий
Множество корней может быть записано по-другому.
Отбор корней может быть произведён любым другим способом: с помощью графика, решения двойных неравенств и т. п.
При отборе корней с помощью числовой (тригонометрической) окружности на числовой окружности должно быть: отмечены и обозначены концы числового отрезка, выделена дуга, отмечены и обозначены корни, принадлежащие данному отрезку. На окружности могут быть отмечены вспомогательные числа, принадлежащие числовому отрезку.
Задание 1
а) Решите уравнение
 .
.
б) Укажите корни этого уравнения, принадлежащие отрезку  .
.
Решение.
а) Запишем исходное уравнение в виде:
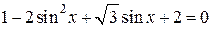 ;
; 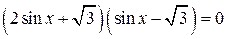 .
.
Значит,  , откуда
, откуда 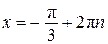 ,
, 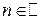 , или
, или  ,
,  .
.
Уравнение  корней не имеет.
корней не имеет.
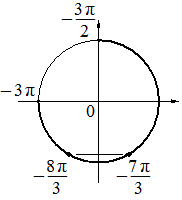
|
б) С помощью числовой окружности отберём корни, принадлежащие отрезку  .
.
Получим числа:  ;
;  .
.
Ответ: а) 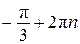 ,
, 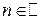 ;
; 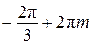 ,
,  ; б)
; б)  ;
;  .
.
| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 2 |
|
|
|
Задание 2
а) Решите уравнение
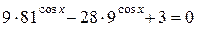 .
.
б) Укажите корни этого уравнения, принадлежащие отрезку  .
.
Решение.
а) Пусть 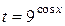 , тогда уравнение запишется в виде
, тогда уравнение запишется в виде 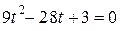 , откуда
, откуда  или
или 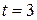 .
.
При  получим:
получим:  ;
; 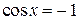 , откуда
, откуда 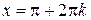 ,
, 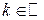 .
.
При 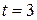 получим:
получим:  ;
; 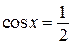 , откуда
, откуда  ,
,  , или
, или  ,
, 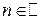 .
.

|
б) С помощью числовой окружности отберём корни, принадлежащие отрезку  .
.
Получим числа: 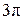 ;
;  .
.
Ответ: а)  ,
, 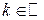 ;
; 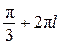 ,
,  ;
; 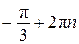 ,
, 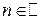 ; б)
; б) 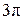 ;
;  .
.
| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 2 |
Задание 3
а) Решите уравнение
 .
.
б) Укажите корни этого уравнения, принадлежащие отрезку  .
.
Решение.
а) Пусть 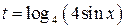 , тогда исходное уравнение запишется в виде
, тогда исходное уравнение запишется в виде  , откуда
, откуда 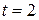 или
или  .
.
При 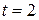 получим:
получим:  , значит,
, значит, 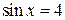 , что невозможно.
, что невозможно.
При  получим:
получим: 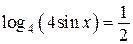 , значит,
, значит,  , откуда
, откуда 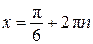 ,
, 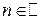 , или
, или  ,
,  .
.

|
б) С помощью числовой окружности отберём корни, принадлежащие отрезку  .
.
Получим число 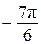 .
.
Ответ: а)  ,
, 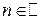 ;
;  ,
,  ; б)
; б) 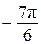 .
.
| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов – пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 2 |
Задание 4
а) Решите уравнение
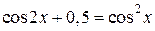 .
.
б) Укажите корни этого уравнения, принадлежащие отрезку  .
.
Решение.
а) Запишем исходное уравнение в виде:
 ;
;  .
.
Значит, или 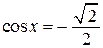 , откуда
, откуда 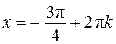 ,
, 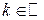 , или
, или 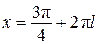 ,
,  , или
, или 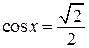 , откуда
, откуда  ,
, 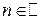 , или
, или 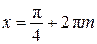 ,
,  .
.
|
|
|
|
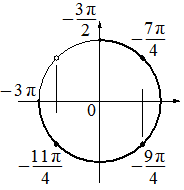
б) С помощью числовой окружности отберём корни, принадлежащие отрезку  .
.
Получим числа: 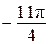 ;
;  ;
; 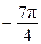 .
.
Ответ: а)  ,
, 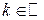 ;
;  ,
,  ;
;  ,
, 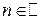 ;
; 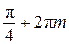 ,
,  ;
;
Ответ: б) 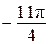 ;
;  ;
; 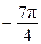 .
.
| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 2 |
|
|
|


