 |
Комментарий. Пример 13.6. Основанием четырёхугольной пирамиды является трапеция , причём. Оценка эксперта: 2 балла. Основанием четырёхугольной пирамиды является трапеция , причём
|
|
|
|
Комментарий
Утверждение в пункте а не доказано. В решении пункта б есть ошибочное утверждение, что привело к неверному ответу.
Оценка эксперта: 0 баллов.
Пример 13. 6
Основанием четырёхугольной пирамиды 
является трапеция 
, причём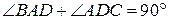 
. Плоскости 
и 
перпендикулярны плоскости основания,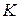 
– точка пересечения прямых 
и 
.
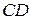а) Докажите, что плоскости и перпендикулярны.
б) Найдите объём пирамиды 
, если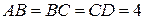 
, а высота пирамиды равна 9.
Ответ: б) 12.
Комментарий
Утверждение в пункте а не доказано. В решении пункта б обоснованно получен верный ответ.
Оценка эксперта: 2 балла.
Пример 13. 7
В правильной четырёхугольной пирамиде 
сторона основания равна 6, а боковое ребро 
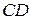равно 7. На рёбрах и 
отмечены точк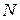и 
и 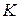соответственно, причём 
. Плоскость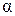 
содержит прямую 
и параллельна прямой .
а) Докажите, что плоскость 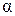параллельна прямой 
.
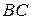б) Найдите расстояние от точки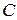 
до плоскости .
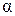Ответ: б) 
.
Комментарий
Утверждение в пункте а доказано. В решении есть неточности в обозначении длин отрезков на первом чертеже и неоднозначность использования ссылки на теорему Фалеса. Решение пункта б не закончено.
Оценка эксперта: 1 балл.
Пример 13. 8
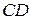В правильной четырёхугольной пирамиде сторона основания равна 6, а боковое ребро равно 7. На рёбрах и отмечены точк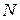и и 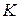соответственно, причём . Плоскость 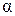содержит прямую и параллельна прямой .
а) Докажите, что плоскость 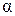параллельна прямой .
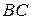б) Найдите расстояние от точки 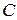до плоскости .
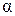Ответ: б) .
Комментарий
Утверждение в пункте а доказано. В решении пункта б есть неточность в решении системы уравнений (выражение С через А), а при применении формулы расстояния от точки до плоскости неверно найден модуль вектора нормали (не относится к вычислительной ошибке).
|
|
|
Оценка эксперта: 1 балл.
3. Критерии проверки и оценка решений задания 14
Задание № 14 – это неравенство: дробно-рациональное, логарифмическое или показательное.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного исключением/ включением граничных точек, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки в строгости неравенства: « 
» вместо « 
» или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять выставить оценку «0 баллов».
Задача 14 (демонстрационный вариант 2022 г. )
Решите неравенство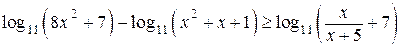 
.
Решение. Правая часть неравенства определена при 
и 
.
Поскольку при любых значениях 
выражение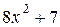 
принимает положительные значения, при и неравенство принимает вид:
; 
; 
; 
,
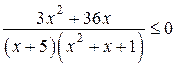откуда 
; 
. Учитывая ограничения и , получаем: ; 
.
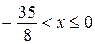Ответ: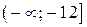 
; 
.
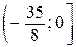| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
Обоснованно получен ответ, отличающийся от верного исключением точек  и/или 0,
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения
| |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 2 |
Задание 1
Решите неравенство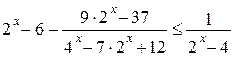 
.
Решение.
Пусть 
, тогда неравенство примет вид:
|
|
|
; 
;
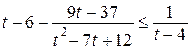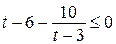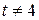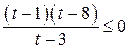, где 
; 
, где ,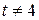
откуда 
; 
; 
.
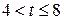При получим: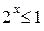 
, откуда 
.
При получим: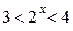 
, откуда 
.
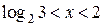При 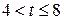получим: 
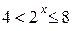, откуда 
.
Решение исходного неравенства:
; ; .
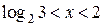Ответ: 
; 
; 
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного исключением точек 0 и/или 3, ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 2 |
|
|
|
