 |
Задача 15 (демонстрационный вариант 2022 г.)
|
|
|
|
Задача 15 (демонстрационный вариант 2022 г. )
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн руб. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на 
процентов по сравнению с концом предыдущего месяца, где – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15. 01 | 15. 02 | 15. 03 | 15. 04 | 15. 05 | 15. 06 | 15. 07 |
| Долг (в млн руб. ) | 0, 6 | 0, 4 | 0, 3 | 0, 2 | 0, 1 |
Найдите наибольшее значение , при котором общая сумма выплат будет меньше 1, 2 млн руб.
Решение. По условию, долг перед банком (в млн руб. ) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:
1; 0, 6; 0, 4; 0, 3; 0, 2; 0, 1; 0.
Пусть 
, тогда долг на 1-е число каждого месяца равен:
; 
; 
; 
; 
; 
.
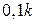Следовательно, выплаты со 2-го по 14-е число каждого месяца составляют:
; 
; 
; 
; 
; .
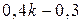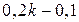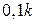Общая сумма выплат составляет:
По условию, общая сумма выплат будет меньше 1, 2 млн руб., значит,
; 
; 
.
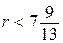Наибольшее целое решение этого неравенства – число 7. Значит, искомое число процентов – 7.
Ответ: 7.
Задание 1
15 января планируется взять кредит в банке на шесть месяцев в размере 1 млн руб. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на процентов по сравнению с концом предыдущего месяца, где – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
| Дата | 15. 01 | 15. 02 | 15. 03 | 15. 04 | 15. 05 | 15. 06 | 15. 07 |
| Долг (в млн руб. ) | 0, 9 | 0, 8 | 0, 7 | 0, 6 | 0, 5 |
Найдите наименьшее значение , при котором общая сумма выплат будет больше 1, 2 млн руб.
|
|
|
Решение.
По условию, долг перед банком (в млн руб. ) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом:
1; 0, 9; 0, 8; 0, 7; 0, 6; 0, 5; 0.
Пусть , тогда долг на 1-е число каждого месяца равен:
; 
; 
; 
; ; 
.
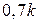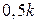Следовательно, выплаты со 2-го по 14-е число каждого месяца составляют:
; 
; 
; 
; 
; .
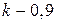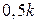Общая сумма выплат составляет:
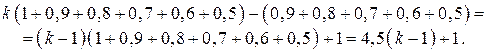
По условию, общая сумма выплат будет больше 1, 2 млн руб., значит,
; 
; 
.
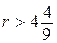Наименьшее целое решение этого неравенства – число 5. Значит, искомое число процентов – 5.
Ответ: 5.
Задание 2
В июле 2021 г. планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
– каждый январь долг увеличивается на 
% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 руб., то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 руб., то кредит будет полностью погашен за 2 года. Найдите .
Решение.
Пусть сумма кредита составляет 
руб., а ежегодные выплаты 
руб., 
. По условию, долг перед банком (в рублях) по состоянию на июль должен уменьшаться следующим образом:
, 
, 
, 
, 
.
Таким образом, если долг будет выплачен двумя равными платежами 
, то
.
Если долг будет выплачен четырьмя равными платежами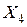 
, то
.
Таким образом, 
, откуда 
; 
. Значит, 
.
Ответ: 10.
Задание 3
15 января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на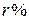 
по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
|
|
|
Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите .
(Считайте, что округления при вычислении платежей не производятся. )
Решение.
Пусть сумма кредита равна . По условию, долг перед банком по состоянию на 15-е число должен уменьшаться до нуля равномерно:
, 
, …, 
, 
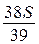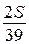, 0.
Первого числа каждого месяца долг возрастает на 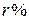. Пусть , тогда последовательность размеров долга на 1-е число каждого месяца такова:
, 
, …, 
, 
.
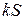Следовательно, выплаты должны быть следующими:
, 
, …, 
, 
.
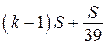Всего следует выплатить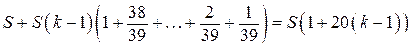 
.
Общая сумма выплат на 20% больше суммы, взятой в кредит, поэтому
; 
; 
.
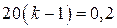Ответ: 1.
|
|
|
