 |
Примеры оценивания решений задания 16
|
|
|
|
Задание 1
В трапеции  боковая сторона
боковая сторона 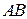 перпендикулярна основаниям.
перпендикулярна основаниям.
Из точки  на сторону
на сторону 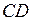 опустили перпендикуляр
опустили перпендикуляр  . На стороне
. На стороне 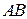 отмечена точка
отмечена точка 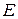 так, что прямые
так, что прямые 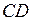 и
и 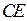 перпендикулярны.
перпендикулярны.
а) Докажите, что прямые 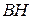 и
и  параллельны.
параллельны.
б) Найдите отношение 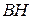 к
к  , если
, если  .
.
Решение.
а) Поскольку
 ,
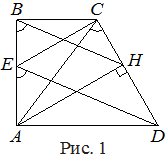
около четырёхугольников ,
около четырёхугольников  и и  можно описать окружности (рис. 1).
Значит, можно описать окружности (рис. 1).
Значит,
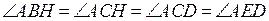 ,
то есть прямые ,
то есть прямые 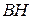 и и  параллельны. параллельны.
| 
|
б) Опустим из точки 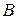 перпендикуляр перпендикуляр  на прямую на прямую 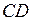 (рис. 2). Стороны (рис. 2). Стороны  и и 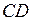 треугольников треугольников  и и  лежат на одной прямой, а стороны лежат на одной прямой, а стороны  и и  , , 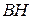 и и  попарно параллельны. Значит, треугольники попарно параллельны. Значит, треугольники  и и  подобны.
Поскольку подобны.
Поскольку
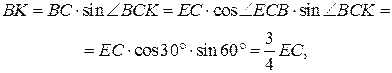
| 
|
коэффициент подобия равен  . Значит,
. Значит,
 .
.
Ответ: б) 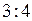 .
.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | |
| Обоснованно получен верный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 3 |
Задание 2
В равнобедренном тупоугольном треугольнике 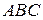 на продолжение боковой стороны
на продолжение боковой стороны 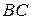 опущена высота
опущена высота  . Из точки
. Из точки 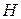 на сторону
на сторону  и основание
и основание  опущены перпендикуляры
опущены перпендикуляры  и
и  соответственно.
соответственно.
а) Докажите, что отрезки  и
и 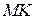 равны.
равны.
б) Найдите 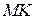 , если
, если 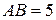 ,
,  .
.
|
|
|
Решение.
а) Поскольку 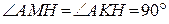 , около четырёхугольника , около четырёхугольника  можно описать окружность с диаметром можно описать окружность с диаметром  . Получаем: . Получаем:
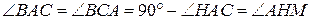 ,
поэтому ,
поэтому  как хорды, стягивающие равные дуги. как хорды, стягивающие равные дуги.
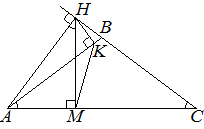
| 
|
б) В прямоугольных треугольниках  и
и 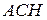 имеем:
имеем:
 .
.
Поскольку 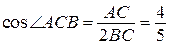 , получаем:
, получаем:
 .
.
Ответ: б)  .
.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | |
| Обоснованно получен верный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 3 |
Задание 3
В остроугольном треугольнике 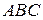 все стороны различны. Прямая, содержащая высоту
все стороны различны. Прямая, содержащая высоту  треугольника
треугольника 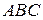 , вторично пересекает описанную около этого треугольника окружность в точке
, вторично пересекает описанную около этого треугольника окружность в точке 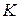 . Отрезок
. Отрезок 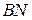 – диаметр этой окружности.
– диаметр этой окружности.
а) Докажите, что 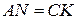 .
.
б) Найдите 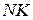 , если радиус описанной около треугольника
, если радиус описанной около треугольника 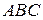 окружности равен 16,
окружности равен 16,  ,
,  .
.
Решение.

|
а) Поскольку 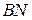 – диаметр описанной около треугольника
– диаметр описанной около треугольника 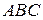 окружности, получаем
окружности, получаем
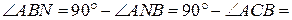
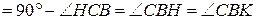 .
.
Следовательно, хорды 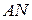 и
и 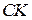 стягивают равные дуги, а значит, они равны.
стягивают равные дуги, а значит, они равны.
б) Пусть  – радиус окружности, описанной около треугольника
– радиус окружности, описанной около треугольника 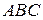 . Имеем:
. Имеем:
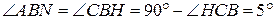 ,
,
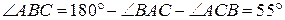 ;
;
 .
.
Следовательно, по теореме синусов
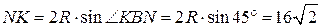 .
.
Ответ: б)  .
.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б | |
| Обоснованно получен верный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 3 |
|
|
|
Примеры оценивания решений задания 16
|
|
|


