 |
Пример 17.1. Оценка эксперта: 4 балла. Обоснованно получен верный ответ. . Комментарий. Оценка эксперта: 0 баллов.
|
|
|
|
Пример 17. 1
Найдите все значения  , при каждом из которых уравнение
, при каждом из которых уравнение

имеет ровно три различных корня.
Ответ:  ;
;  ;
;  .
.

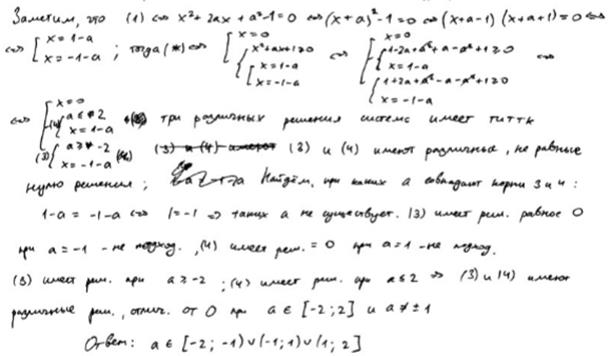
Комментарий
Обоснованно получен верный ответ.
Оценка эксперта: 4 балла.
Пример 17. 2
Найдите все значения  , при каждом из которых уравнение
, при каждом из которых уравнение

имеет ровно три различных корня.
Ответ:  ;
;  ;
;  .
.


Комментарий
Решение логично, все шаги присутствуют, но при решении неравенства в пункте 2 допущена ошибка вычислительного характера, что соответствует критерию на 2 балла.
Оценка эксперта: 2 балла.
Пример 17. 3
Найдите все значения  , при каждом из которых уравнение
, при каждом из которых уравнение

имеет ровно три различных корня.
Ответ:  ;
;  ;
;  .
.



Комментарий
Получены корни уравнения 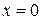 ,
, 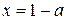 ,
, 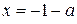 и задача сведена к исследованию полученных корней при условии
и задача сведена к исследованию полученных корней при условии  (есть только указание).
(есть только указание).
Оценка эксперта: 1 балл.
Пример 17. 4
Найдите все значения  , при каждом из которых уравнение
, при каждом из которых уравнение

имеет ровно три различных корня.
Ответ:  ;
;  ;
;  .
.


Комментарий
В решении присутствуют все этапы. Решение соответствует критерию на 3 балла: с помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек  и/или
и/или 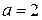 .
.
Оценка эксперта: 3 балла.
Пример 17. 5
Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений
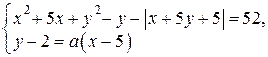
имеет ровно два решения.
Ответ:  .
.


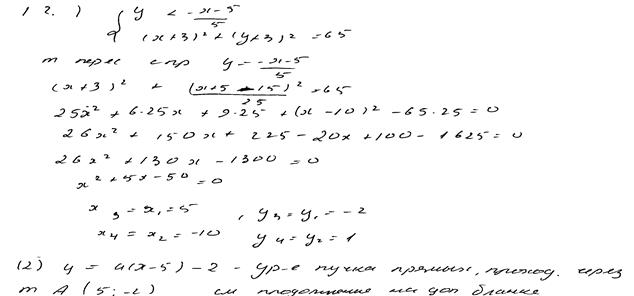
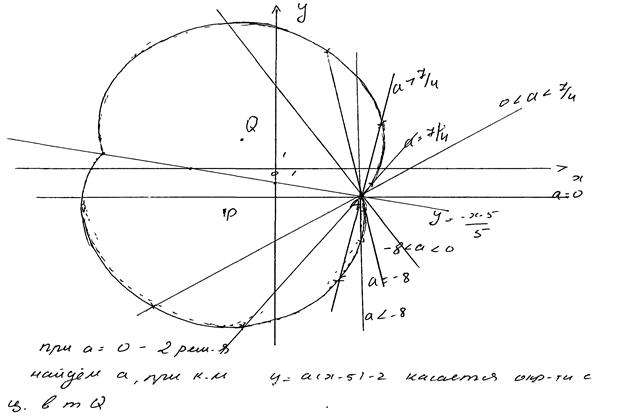



Комментарий
Ход решения ясен, изложен более чем подробно. Ошибок нет, кроме недочёта: концы промежутка не включены в ответ.
Оценка эксперта: 3 балла.
Пример 17. 6
Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений
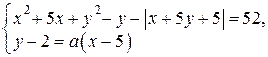
имеет ровно два решения.
Ответ:  .
.
|
|
|
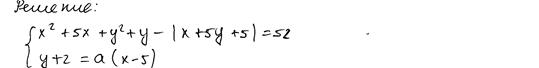

Комментарий
Решение и ответ верные, хотя нет обоснования, почему для касания  «
«  должно быть равно –8» или «…7/4».
должно быть равно –8» или «…7/4».
Оценка эксперта: 4 балла.
Пример 17. 7
Найдите все значения a, при каждом из которых уравнение

имеет ровно два различных корня.
Ответ:  ;
; 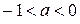 ;
;  ;
;  ;
;  .
.
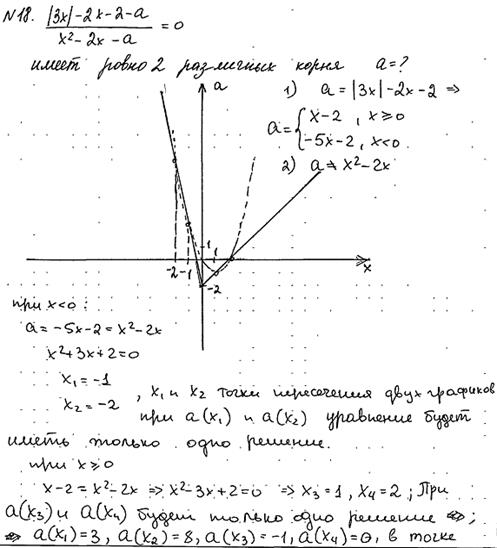

Комментарий
Обоснованно получен верный ответ.
Оценка эксперта: 4 балла.
Пример 17. 8
Найдите все значения a, при каждом из которых уравнение

имеет ровно два различных корня.
Ответ:  ;
; 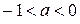 ;
;  ;
;  ;
;  .
.


Комментарий
Неверное решение уравнения, содержащего переменную под знаком модуля. Неверная логика исследования количества корней.
Оценка эксперта: 0 баллов.
7. Критерии проверки и оценка решений заданий 18
Задание 18 проверяет достижение следующих целей изучения математики на профильном уровне: «развитие логического мышления, алгоритмической культуры, пространственного воображения, математического мышления и интуиции, творческих способностей, необходимых для продолжения образования и для самостоятельной деятельности в области математики и её приложений в будущей профессиональной деятельности».
При этом, для решения этой задачи не требуется никаких знаний, выходящих за рамки школьного курса.
Условие задания 18 разбито на пункты – ряд подзадач (частных случаев), последовательно решая которые, можно в итоге полностью выполнить задание. Такое разбиение, в первую очередь, облегчает участнику экзамена планирование работы над данной задачей, а также позволяет более чётко и прозрачно провести оценивание выполнения задания.
Задача 18 (демонстрационный вариант 2022 г. )
В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
|
|
|
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Решение. а) Пусть в школе № 1 писали тест 2 учащихся, один из них набрал
1 балл, а второй набрал 19 баллов и перешёл в школу № 2. Тогда средний балл в школе № 1 уменьшился в 10 раз.
б) Пусть в школе № 2 писали тест 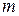 учащихся, средний балл равнялся
учащихся, средний балл равнялся  , а перешедший в неё учащийся набрал
, а перешедший в неё учащийся набрал  баллов. Тогда получаем:
баллов. Тогда получаем:
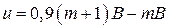 ;
; 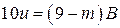 .
.
Если  , то
, то 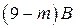 не делится на 10, а
не делится на 10, а 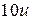 делится на 10. Но это невозможно, поскольку
делится на 10. Но это невозможно, поскольку 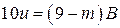 .
.
в) Пусть в школе № 1 средний балл равнялся  . Тогда получаем:
. Тогда получаем:
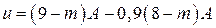 ;
;  .
.
Заметим, что если  или
или 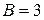 , то
, то 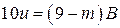 не делится на 10. Если
не делится на 10. Если 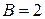 или
или 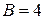 , то
, то  . В первом случае
. В первом случае  , а во втором
, а во втором  . Значит, ни один из этих случаев не возможен.
. Значит, ни один из этих случаев не возможен.
При  и
и 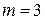 получаем
получаем 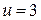 и
и 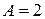 . Этот случай реализуется, например, если в школе № 1 писали тест 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла; в школе № 2 писали тест 3 учащихся, и каждый набрал по 5 баллов; у перешедшего из одной школы в другую учащегося – 3 балла.
. Этот случай реализуется, например, если в школе № 1 писали тест 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла; в школе № 2 писали тест 3 учащихся, и каждый набрал по 5 баллов; у перешедшего из одной школы в другую учащегося – 3 балла.
Ответ: а) да; б) нет; в) 5.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: – обоснованное решение пункта а; – обоснованное решение пункта б; – искомая оценка в пункте в; – пример в пункте в, обеспечивающий точность предыдущей оценки | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 4 |
|
|
|


