 |
Примеры оценивания решений задания 17
|
|
|
|
Задание 1
Найдите все значения  , при каждом из которых уравнение
, при каждом из которых уравнение
 имеет ровно три различных корня.
имеет ровно три различных корня.
Решение. Исходное уравнение равносильно уравнению  при условии
при условии  .
.
Решим уравнение  :
:
 ;
;  ;
;  , откуда
, откуда 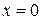 ,
, 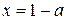 или
или 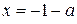 .
.
Исходное уравнение имеет три корня, когда эти числа различны и для каждого из них выполнено условие  .
.
Рассмотрим условия совпадения корней. При  имеем
имеем  . При
. При  имеем
имеем  . При остальных значениях
. При остальных значениях  числа 0,
числа 0, 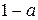 ,
,  различны.
различны.
При 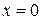 получаем:
получаем:  при всех значениях
при всех значениях  .
.
При 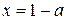 получаем:
получаем:  .
.
Это выражение неотрицательно при  .
.
При 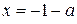 получаем:
получаем:  .
.
Это выражение неотрицательно при  .
.
Таким образом, исходное уравнение имеет ровно три различных корня при
 ;
;  ;
;  .
.
Ответ:  ;
;  ;
;  .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек a = –2 и/или a = 2 | |
| С помощью верного рассуждения получен промежуток (–2; 2) множества значений a, возможно, с включением граничных точек ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | |
Получены корни уравнения  : : 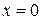 , , 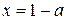 , , 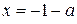 и задача верно сведена к исследованию полученных корней при условии и задача верно сведена к исследованию полученных корней при условии  ( (  ) )
| |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 4 |
Задание 2
Найдите все значения  , при каждом из которых система уравнений
, при каждом из которых система уравнений
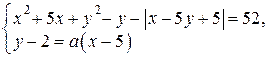
имеет ровно два решения.
Решение.
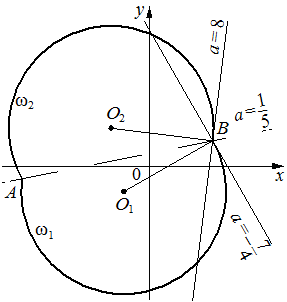
|
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим два случая:
1) Если 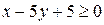 , то получаем уравнение
, то получаем уравнение
 ;
;
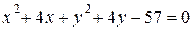 ;
;
 .
.
Полученное уравнение задаёт окружность с центром в точке 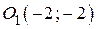 и радиусом
и радиусом  .
.
|
|
|
2) Если 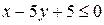 , то получаем уравнение
, то получаем уравнение
 ;
; 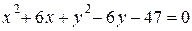 ;
; 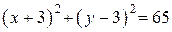 .
.
Полученное уравнение задаёт окружность с центром в точке 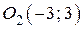
и радиусом  .
.
Полученные окружности пересекаются в двух точках 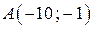 и
и 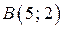 , лежащих на прямой
, лежащих на прямой  , поэтому в первом случае получаем дугу
, поэтому в первом случае получаем дугу  с концами в точках
с концами в точках  и
и  , во втором – дугу
, во втором – дугу  с концами в тех же точках (см. рисунок).
с концами в тех же точках (см. рисунок).
Рассмотрим второе уравнение системы. Оно задаёт прямую 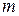 , которая проходит через точку
, которая проходит через точку  , и угловой коэффициент которой равен
, и угловой коэффициент которой равен 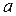 .
.
При 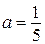 прямая
прямая 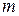 проходит через точки
проходит через точки  и
и  , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
При  прямая
прямая 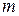 перпендикулярна прямой
перпендикулярна прямой 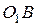 , угловой коэффициент которой равен
, угловой коэффициент которой равен 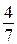 , значит, прямая
, значит, прямая 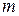 касается дуги
касается дуги  в точке
в точке  и пересекает дугу
и пересекает дугу  в двух точках (одна из которых – точка
в двух точках (одна из которых – точка  ), то есть исходная система имеет два решения.
), то есть исходная система имеет два решения.
При  прямая
прямая 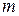 перпендикулярна прямой
перпендикулярна прямой  , угловой коэффициент которой равен
, угловой коэффициент которой равен 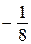 , значит, прямая
, значит, прямая 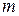 касается дуги
касается дуги  в точке
в точке  и пересекает дугу
и пересекает дугу  в двух точках (одна из которых – точка
в двух точках (одна из которых – точка  ), то есть исходная система имеет два решения.
), то есть исходная система имеет два решения.
При  или
или 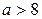 прямая
прямая 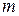 пересекает каждую из дуг
пересекает каждую из дуг  и
и  в точке
в точке  и ещё в одной точке, отличной от точки
и ещё в одной точке, отличной от точки  , то есть исходная система имеет три решения.
, то есть исходная система имеет три решения.
При  прямая
прямая 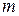 пересекает дугу
пересекает дугу  в двух точках (одна из которых – точка
в двух точках (одна из которых – точка  ) и не пересекает дугу
) и не пересекает дугу  в точках, отличных от точки
в точках, отличных от точки  , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
При 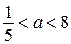 прямая
прямая 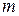 пересекает дугу
пересекает дугу  в двух точках (одна из которых – точка
в двух точках (одна из которых – точка  ) и не пересекает дугу
) и не пересекает дугу  в точках, отличных от точки
в точках, отличных от точки  , то есть исходная система имеет два решения.
, то есть исходная система имеет два решения.
Значит, исходная система имеет ровно два решения при 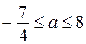 .
.
Ответ: 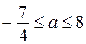 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только исключением точек  и/или и/или 
| |
| При всех значениях a верно найдено количество решений системы в одном из двух случаев, возникающих при раскрытии модуля ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения | |
| Задача верно сведена к исследованию взаимного расположения дуг окружностей и прямых (аналитически или графически) | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 4 |
|
|
|
Задание 3
Найдите все значения a, при каждом из которых уравнение

имеет ровно два различных корня.
Решение.
Корнями исходного уравнения являются корни уравнения  , для которых выполнено условие
, для которых выполнено условие  .
.
При  уравнение
уравнение  принимает вид
принимает вид 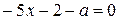 и задаёт на плоскости
и задаёт на плоскости 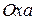 луч
луч  с началом в точке
с началом в точке  . При
. При  уравнение
уравнение  принимает вид
принимает вид 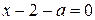 и задаёт луч
и задаёт луч  с началом в точке
с началом в точке  . Значит, уравнение
. Значит, уравнение  имеет два корня при
имеет два корня при 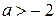 , имеет один корень при
, имеет один корень при  и не имеет корней при
и не имеет корней при  .
.
Уравнение  задаёт параболу
задаёт параболу 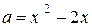 .
.
Координаты точек пересечения параболы 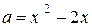 с лучом
с лучом  являются решениями системы:
являются решениями системы:
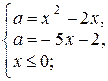

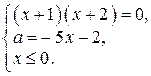
Значит, парабола 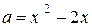 пересекается с лучом
пересекается с лучом  в точках
в точках 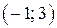 и
и  .
.
Координаты точек пересечения параболы 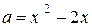 с лучом
с лучом  являются решениями системы:
являются решениями системы:



Значит, парабола 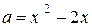 пересекается с лучом
пересекается с лучом  в точках
в точках  и
и 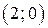 .
.
Следовательно, условие  выполнено для корней уравнения
выполнено для корней уравнения  при всех
при всех  , кроме
, кроме 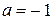 ,
, 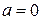 ,
, 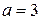 и
и  .
.
Таким образом, исходное уравнение имеет ровно два корня при  ;
; 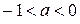 ;
;  ;
;  ;
;  .
.
Ответ:  ;
; 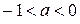 ;
;  ;
;  ;
;  .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
С помощью верного рассуждения получено множество значений a, отличающееся от искомого только включением точки 
| |
Верно рассмотрен хотя бы один из случаев решения, и получено или множество значений a, отличающееся от искомого только включением точек  , , 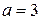 и/или и/или  , или множество значений a, отличающееся от искомого только включением точек , или множество значений a, отличающееся от искомого только включением точек 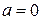 , , 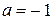 и/или и/или  ,
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения ,
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом верно выполнены все шаги решения
| |
| Задача верно сведена к исследованию взаимного расположения параболы и лучей (аналитически или графически) | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 4 |
Примеры оценивания решений задания 17
|
|
|


