 |
Комментарий. Пример 16.8. В остроугольном треугольнике все стороны различны. Прямая, содержащая высоту треугольника , вторично пересекает описанную около этого треугольника окружность в точке. Отрезок – диаметр этой
|
|
|
|
Комментарий
В доказательстве утверждения пункта а есть верное название прямого угла – « 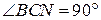 », при этом тут же записано противоречащее условию утверждение «BH – диаметр». Утверждение, записанное во второй строчке – «
», при этом тут же записано противоречащее условию утверждение «BH – диаметр». Утверждение, записанное во второй строчке – « 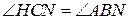 (т. к. они опираются на одну дугу)», – содержит неточность, поскольку точка H не лежит на окружности, а
(т. к. они опираются на одну дугу)», – содержит неточность, поскольку точка H не лежит на окружности, а 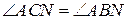 (так как они опираются на одну дугу). Решение пункта б отсутствует.
(так как они опираются на одну дугу). Решение пункта б отсутствует.
Оценка эксперта: 1 балл.
Пример 16. 8
В остроугольном треугольнике 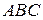 все стороны различны. Прямая, содержащая высоту
все стороны различны. Прямая, содержащая высоту  треугольника
треугольника 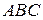 , вторично пересекает описанную около этого треугольника окружность в точке
, вторично пересекает описанную около этого треугольника окружность в точке 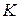 . Отрезок
. Отрезок 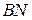 – диаметр этой окружности.
– диаметр этой окружности.
а) Докажите, что 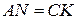 .
.
б) Найдите 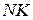 , если радиус описанной около треугольника
, если радиус описанной около треугольника 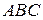 окружности равен 16,
окружности равен 16,  ,
,  .
.
Ответ: б)  .
.

Комментарий
При выполнении пункта а используется недоказанное утверждение, что  – трапеция. В решении есть некорректное утверждение: «по свойству трапеции, вписанной в окружность, её стороны равны», при этом рядом записано верное равенство боковых сторон. Решение пункта б отсутствует.
– трапеция. В решении есть некорректное утверждение: «по свойству трапеции, вписанной в окружность, её стороны равны», при этом рядом записано верное равенство боковых сторон. Решение пункта б отсутствует.
Оценка эксперта: 1 балл.
6. Критерии проверки и оценка решений задания 17
Задание № 17 – это уравнение, неравенство или их системы с параметром.
Задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространёнными из них являются:
– чисто алгебраический способ решения;
– способ решения, основанный на построении и исследовании геометрической модели данной задачи;
– функциональный способ, в котором могут быть и алгебраические, и геометрические элементы, но базовым является исследование некоторой функции.
Зачастую (но далеко не всегда) графический метод более ясно ведёт к цели. Кроме того, в конкретном тексте решения вполне могут встречаться элементы каждого из трёх перечисленных способов.
|
|
|
Задача 17 (демонстрационный вариант 2022 г. )
Найдите все положительные значения  , при каждом из которых система
, при каждом из которых система
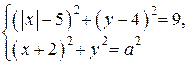
имеет единственное решение.
Решение.
Если  , то уравнение
, то уравнение 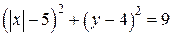 задаёт окружность
задаёт окружность  с центром в точке
с центром в точке 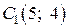 радиусом
радиусом 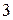 , а если
, а если 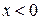 , то оно задаёт окружность
, то оно задаёт окружность  с центром в точке
с центром в точке  и таким же радиусом (см. рисунок).
и таким же радиусом (см. рисунок).
При положительных значениях  уравнение
уравнение 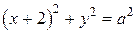 задаёт окружность
задаёт окружность 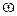 с центром в точке
с центром в точке  радиусом
радиусом  . Поэтому задача состоит в том, чтобы найти все значения
. Поэтому задача состоит в том, чтобы найти все значения  , при каждом из которых окружность
, при каждом из которых окружность 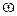 имеет единственную общую точку с объединением окружностей
имеет единственную общую точку с объединением окружностей  и
и  .
.

Из точки 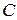 проведём луч
проведём луч 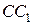 и обозначим через
и обозначим через 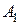 и
и 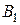 точки его пересечения с окружностью
точки его пересечения с окружностью  , где
, где 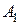 лежит между
лежит между 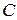 и
и  . Так как
. Так как
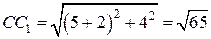 , то
, то 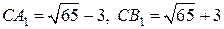 .
.
При 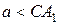 или
или  окружности
окружности 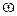 и
и  не пересекаются.
не пересекаются.
При  окружности
окружности 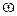 и
и  имеют две общие точки.
имеют две общие точки.
При 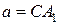 или
или  окружности
окружности 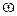 и
и  касаются.
касаются.
Из точки 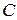 проведём луч
проведём луч 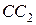 и обозначим через
и обозначим через  и
и  точки его пересечения с окружностью
точки его пересечения с окружностью  , где
, где  лежит между
лежит между 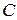 и
и 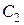 . Так как
. Так как 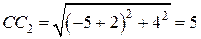 , то
, то  .
.
При  или
или 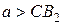 окружности
окружности 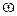 и
и  не пересекаются.
не пересекаются.
При  окружности
окружности 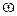 и
и  имеют две общие точки.
имеют две общие точки.
При  или
или  окружности
окружности 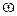 и
и  касаются.
касаются.
Исходная система имеет единственное решение тогда и только тогда, когда окружность  касается ровно одной из двух окружностей
касается ровно одной из двух окружностей  и
и  и не пересекается с другой. Так как
и не пересекается с другой. Так как 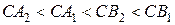 , то условию задачи удовлетворяют только числа
, то условию задачи удовлетворяют только числа 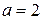 и
и  .
.
Ответ: 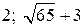 .
.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| С помощью верного рассуждения получены оба верных значения параметра, но – или в ответ включены также и одно-два неверных значения; – или решение недостаточно обосновано | |
| С помощью верного рассуждения получено хотя бы одно верное значение параметра | |
| Задача сведена к исследованию: – или взаимного расположения трёх окружностей; – или двух квадратных уравнений с параметром | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл | 4 |
|
|
|
|
|
|


