 |
Пример 18.1. Оценка эксперта: 1 балл. в) Из какого наименьшего числа членов может состоять такая последовательность?. Оценка эксперта: 2 балла.
|
|
|
|
Пример 18. 1
В последовательности 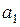 ,
,  , …,
, …,  ,
,  , состоящей из целых чисел,
, состоящей из целых чисел,  ,
, 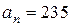 . Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
. Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Ответ: а) например, 1, 2, 3, 0, 5,  , 7,
, 7, 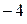 , …, 233,
, …, 233,  , 235; б) нет; в) 23.
, 235; б) нет; в) 23.

Комментарий
В пункте а допущена ошибка: сумма первых двух чисел равна –25. При ответе на вопрос пункта б участник экзамена верно показал, что случай 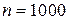 невозможен.
невозможен.
Оценка эксперта: 1 балл.
Пример 18. 2
В последовательности 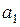 ,
,  , …,
, …,  ,
,  , состоящей из целых чисел,
, состоящей из целых чисел,  ,
, 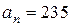 . Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
. Сумма любых двух соседних членов последовательности равна 3, 5 или 25.
а) Приведите пример такой последовательности.
б) Может ли такая последовательность состоять из 1000 членов?
в) Из какого наименьшего числа членов может состоять такая последовательность?
Ответ: а) например, 1, 2, 3, 0, 5,  , 7,
, 7, 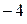 , …, 233,
, …, 233,  , 235; б) нет; в) 23.
, 235; б) нет; в) 23.

Комментарий
В пункте а верно приведён пример. Решение пункта б неверно.
Оценка эксперта: 1 балл.
Пример 18. 3
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 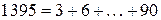 , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
|
|
|
Ответ: а) да; б) нет; в) 6.


Комментарий
Приведено верное решение пункта а. Приведено верное решение пункта б. Решение в пункте в не завершено.
Оценка эксперта: 2 балла.
Пример 18. 4
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 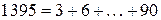 , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Ответ: а) да; б) нет; в) 6.


Комментарий
Обоснованно получены верные ответы во всех пунктах.
Оценка эксперта: 4 балла.
Пример 18. 5
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше 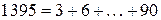 , если все числа на доске кратны 3?
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Ответ: а) да; б) нет; в) 6.

Комментарий
Обоснованно получен ответ в пунктах а и б. В решении пункта в есть логическая ошибка: не доказано, что красных чисел не может быть меньше 5. Взяв 5 красных чисел, нужно взять 25 зелёных чисел, а не 26. Кроме того, сумма чисел найдена неверно.
|
|
|
|
|
|


