 |
Оценка эксперта: 2 балла. Пример 18.6. б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
|
|
|
|
Оценка эксперта: 2 балла.
Пример 18. 6
На доске написано 30 натуральных чисел (числа могут повторяться), каждое из которых либо зелёного, либо красного цвета. Каждое зелёное число кратно 3, а каждое красное число кратно 7. При этом все зелёные числа различны и все красные различны (какое-то зелёное число может равняться какому-то красному числу).
а) Может ли сумма написанных чисел быть меньше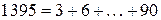 
, если все числа на доске кратны 3?
б) Может ли ровно одно число на доске быть красным, если сумма написанных чисел равна 1067?
в) Какое наименьшее количество красных чисел может быть на доске, если сумма написанных чисел равна 1067?
Ответ: а) да; б) нет; в) 6.
Комментарий
Обоснованно получен ответ в пунктах а и б. В пункте в неверное обоснование, поскольку не доказано, что набор с минимальным количеством красных чисел получается заменой максимальных чисел из набора 3, 6, ..., 90 на минимально возможные различные красные числа. Кроме того, разница между пятью самыми большими зелёными числами и пятью самыми маленькими красными числами составляет 315.
Оценка эксперта: 2 балла.
Пример 18. 7
На столе лежит 40 карточек, часть из которых красного цвета, а остальные синего (есть хотя бы по одной карточке каждого цвета). На каждой карточке написано натуральное число. Все числа, написанные на синих карточках, различны. Любое число на красной карточке меньше любого числа на синей карточке. Среднее арифметическое всех чисел на карточках равно 14. Если утроить числа на синих карточках, то среднее арифметическое всех чисел станет равно 39.
а) Может ли на столе быть ровно 10 синих карточек?
б) Может ли на столе быть ровно 10 красных карточек?
|
|
|
в) Какое наибольшее количество синих карточек может быть на столе?
Ответ: а) да; б) нет; в) 26.
Комментарий
В решении пункта а приведён пример чисел на синих карточках, в котором есть повторяющееся число 21, да и сумма этих чисел равна 495, а не 500. Обоснованно получен ответ в пункте б. Решение пункта в фактически отсутствует, да и сам ответ неверный.
Оценка эксперта: 1 балл.
Пример 18. 8
На столе лежит 40 карточек, часть из которых красного цвета, а остальные синего (есть хотя бы по одной карточке каждого цвета). На каждой карточке написано натуральное число. Все числа, написанные на синих карточках, различны. Любое число на красной карточке меньше любого числа на синей карточке. Среднее арифметическое всех чисел на карточках равно 14. Если утроить числа на синих карточках, то среднее арифметическое всех чисел станет равно 39.
а) Может ли на столе быть ровно 10 синих карточек?
б) Может ли на столе быть ровно 10 красных карточек?
в) Какое наибольшее количество синих карточек может быть на столе?
Ответ: а) да; б) нет; в) 26.
Комментарий
В решении пункта а есть только описание чисел, написанных на синих карточках. Указание чисел, написанных на красных карточках, отсутствует. В решении пункта б допущена вычислительная ошибка. Решение пункта в отсутствует.
Оценка эксперта: 2 балла.
Указания по оцениванию развёрнутых ответов участников ЕГЭ для эксперта, проверяющего развёрнутые ответы на задания 12–18 по МАТЕМАТИКЕ
(документ предоставляется эксперту при проведении оценивания экзаменационных работ вместе с критериями оценивания)
Эксперт, проверяющий задания с развёрнутым ответом, располагает следующими материалами:
1) текстами заданий;
2) возможным вариантом решения каждой задачи 12–18;
3) критериями оценивания заданий 12–18.
При проверке выполнения заданий с развёрнутым ответом эксперт должен иметь возможность пользоваться непрограммируемым калькулятором[1].
|
|
|
В критериях оценивания выполнения заданий с развёрнутым ответом КИМ ЕГЭ по математике для каждого задания приводится один возможный вариант решения. Однако предлагаемый разработчиками КИМ способ (метод) решения не является эталонным. Он лишь помогает эксперту в решении соответствующего задания.
Выполнение заданий оценивается в соответствии с критериями оценивания ответов на задания с развёрнутым ответом. Принципом построения системы оценивания является оценка продвижений участника экзамена в решении задачи в виде достижения формализованных в критериях промежуточных результатов. Максимальный балл выставляется только при наличии в тексте решения обоснованно полученного правильного ответа. Наличие в тексте решения недостатка в обосновании ответа или вычислительной ошибки не позволяет выставить за решение задания в соответствии с критериями максимальный балл. В случае, когда решение не подпадает ни под один из критериев положительных баллов (не достигнут ни один промежуточный математический результат), выполнение задания оценивается 0 баллов.
При использовании обобщённой схемы оценивания ответов на каждое из заданий 12–18рекомендуется обращать внимание на следующие моменты.
· Перед проведением проверки выполнения каждого из заданий необходимо изучить критерии его оценивания в материалах для эксперта, обратив внимание на детализацию и конкретизацию обобщённой схемы оценивания применительно к конкретному заданию.
· Решение участника экзамена может иметь логику, отличную от логики решения, данного в критериях (альтернативное решение). В этом случае эксперт оценивает допустимость решения конкретной задачи тем способом, который выбрал участник экзамена. Если ход решения допустим, то эксперт оценивает обоснованность этого решения на основании той совокупности свойств (признаков), формул или утверждений, которые соответствуют выбранному способу решения.
· Участник экзамена может использовать без доказательства математические факты и формулы, содержащиеся в учебниках, входящих в федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования (далее – Федеральный перечень).
|
|
|
· Если экзаменуемый использует в решении без доказательства формулы и факты, которые не представлены в учебниках, входящих в Федеральный перечень, то такое решение классифицируется как недостаточно обоснованное.
· Если математические преобразования, представленные в решении, не отражают основных необходимых логических шагов, то решение не может оцениваться максимальным баллом.
· Если при решении геометрической задачи экзаменуемый использует рисунок, то ошибки в соотношении длин отрезков на рисунке не влекут за собой снижения баллов за решение геометрической задачи, если на рисунке верно отображена геометрическая конфигурация и верно обозначены точки, описанные в решении.
· При проверке правильности решения необходимо проверять корректность промежуточных шагов решения, в том числе числовых выкладок (при необходимости – с помощью калькулятора). Наличие ошибок в промежуточных выкладках, даже не повлиявших на итоговый ответ, означает наличие математически некорректного перехода в решении задачи, что не позволяет оценить решение задачи максимальным баллом.
· Если участник экзамена решает задачу с другими числовыми данными, то такое решение задачи оценивается в 0 баллов, даже если он решает содержательно более сложную задачу.
· При проверке решения каждого из заданий 12–18 необходимо вычленить в решении три элемента:
- логику (последовательность и закономерность) решения,
- обоснованность решения,
- числовой ответ.
Количество логических шагов в решении и перечень условий и закономерностей зависит от выбранного способа решения. Это необходимо учитывать при применении критериев оценивания выполнения задания с развёрнутым ответом.
В процессе проверки необходимо придерживаться следующих общих правил.
|
|
|
· При работе эксперт выставляет свои оценки в протокол проверки развёрнутых ответов.
· Выставление баллов в протокол проверки развёрнутых ответов рекомендуется проводить по работам: все задания первой проверяемой работы, все задания второй проверяемой работы и т. д. Это позволяет обнаружить ошибки, допущенные экзаменуемым в нумерации задач, а также обнаружить непронумерованную, или пронумерованную неверно, или случайно пропущенную экспертом задачу. Ошибочное указание участником экзамена номера задачи, которую он выполняет, не может служить основанием для снижения оценки за фактически выполненное задание.
· Результаты оценивания переносятся в протокол проверки развёрнутых ответов, при этом баллы по каждому заданию переносятся в колонку, название которой соответствует номеру задания (рис. 1):
- баллы по заданию 12 переносятся в колонку 12 протокола;
- баллы по заданию 13 переносятся в колонку 13 протокола;
- баллы по заданию 14 переносятся в колонку 14 протокола;
- баллы по заданию 15 переносятся в колонку 15 протокола;
- баллы по заданию 16 переносятся в колонку 16 протокола;
- баллы по заданию 17 переносятся в колонку 17 протокола;
- баллы по заданию 18 переносятся в колонку 18 протокола.
· Баллы выставляются в протокол проверки гелевой чёрной ручкой.
· Внесение изменений в протокол проверки крайне нежелательно. Использование замазок и затирок в целях исправления записей категорически недопустимо!
Рисунок 1. Протокол проверки развёрнутых ответов 2022 года. Образец
Внимание! При выставлении баллов за выполнение задания в Протокол проверки развёрнутых ответов следует иметь в виду, что если ответ отсутствует (нет никаких записей, свидетельствующих о том, что экзаменуемый приступал к выполнению задания), то в протокол проставляется « Х», а не «0». Если в работе записан только номер задания без попыток его выполнения, то в протокол выставляется «0».
[1] Возможность использовать непрограммируемый калькулятор при оценивании экзаменационных работ участников ЕГЭ 2022 г. должна быть закреплена нормативными правовыми актами органа исполнительной власти субъекта Российской Федерации, осуществляющего государственное управление в сфере образования.
|
|
|
