 |
11. АКТИВНЫЕ СРЕДЫ. 11.1. Бистабильные среды. Схема работы ячейки горения. Ячейка горения имеет три стационарных состояния (рис.11.1): Т1 – горение отсутствует, Т3 – устойчивое горение, когда тепловыделение равно теплоотводу, и Т2 – появляется как математ
|
|
|
|
11. АКТИВНЫЕ СРЕДЫ
При анализе динамических моделей химических реакций мы молчаливо предполагали, что диффузия в реакционной зоне может осуществляться достаточно быстро – тогда подвод и отвод компонентов (реагентов) не лимитирует стадию химического реагирования, и система остаётся однородной, то есть гомогенной. Однако диффузию можно считать мгновенной только при высоких температурах или в специальных объектах, в которых есть каналы ускоренной диффузии, обычно же скорость диффузии заметно влияет на кинетику химических реакций, причём это относится не только к химическим системам: аналогичные явления имеют место в непрерывных средах, в которых под влиянием внешних воздействий происходят диссипативные процессы. Среды, в которых процессы диссипации зависят от процессов переноса, называются активными.
Чтобы изучить диссипативные процессы и возможные состояния активных сред, построим упрощённую модель среды: разобьём непрерывную среду на элементы и будем считать, что внешнее воздействие рассредоточено, т. е. каждый элемент можно считать отдельной системой, подверженной воздействию. Тогда запишем динамическую модель для отдельного элемента в привычном виде:
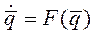. (11. 1)
Так как элементы связаны между собой, то следует учесть наличие потоков Jq, соответствующих типу взаимодействия между элементами (поток тепла, поток вещества, поток зарядов и т. д. ), тогда динамическое уравнение примет следующий вид:
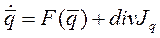
(11. 2)
Для среды, в которой присутствуют потоки диффузионного типа, полученное уравнение приобретёт вид:
|
|
|
, (11. 3)
где D – коэффициенты переноса (коэффициенты диффузии), которые не зависят от пространственных координат.
Отклик среды на внешнее воздействие будет зависеть от характера процессов, происходящих в каждом элементе, т. е. от вида функции Fj и от интенсивности внутренних взаимодействий, мерой которых являются коэффициенты переноса. Разберем поведение активных сред, содержащих два типа элементов (функций Fj), которые соответствуют наиболее часто встречающимся на практике активным средам.
11. 1. Бистабильные среды
Бистабильной называется среда, которая состоит из элементов, имеющих по два устойчивых (стабильных) стационарных состояния, причём переход из одного состояния в другое осуществляется жёстким возбуждением - элементы такой среды называются бистабильными, или триггерными.
Ячейка горения.
Представим себе, что элемент среды – ячейка, в которой происходит процесс горения. При горении выделяется тепло, имеется теплообмен с соседними ячейками. Модель процесса горения, протекающего в ячейке, описывается уравнением теплопроводности:
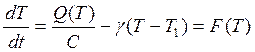, (11. 4)
где Q(T) – теплота горения (Дж/с); С – теплоемкость; γ – коэффициент теплообмена; Т1 – температура окружающей среды.
Рис. 11. 1. Вид динамической функции F(T) для ячейки горения.
Схема работы ячейки горения. Ячейка горения имеет три стационарных состояния (рис. 11. 1): Т1 – горение отсутствует, Т3 – устойчивое горение, когда тепловыделение равно теплоотводу, и Т2 – появляется как математическое следствие двух устойчивых стационарных состояний при Т1 и Т3 (вспомним, что устойчивость стационарных состояний можно определить по знаку тангенса угла наклона функции F(T) в особых точках).
|
|
|
Элемент среды может быть подвержен двум типам жёсткого внешнего воздействия: его можно перевести из состояния Т1 в состояние Т3 (т. е. зажечь) и из состояния Т3 в состояние Т1 (т. е. погасить). Оба воздействия носят характер жесткого возбуждения.
Если учесть взаимодействие таких ячеек, то уравнение теплопроводности следует записать следующим образом:
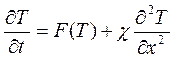, (11. 5)
где 
- коэффициент теплопроводности. Полученное уравнение является модельным для бистабильной среды, содержащей в качестве элементов ячейки горения.
Модель Шлегля
Рассмотрим химический процесс, состоящий из двух звеньев:
А + 2Х 
3Х
Х 
В
Кинетическая модель этого процесса имеет вид
(11. 6)
и носит название модели Шлегля. Рассматриваемая реакция протекает в каждом элементе распределённой среды реагентов. С учетом массопереноса между элементами среды модель следует записать следующим образом:
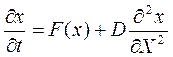, (11. 7)
где Х – координата, вдоль которой распространяется взаимодействие элементов среды. Функция F(x) имеет 3 стационарных состояния и геометрически выглядит также, как F(Т) для ячейки горения. Реакцию можно жестким возбуждением запустить, подав в реакционную зону количество реагента х, большее некоторого порогового значения, или остановить, выведя весь реагент х из реакционной зоны.
Запишем общий для рассмотренных трёх случаев вид модели бистабильной среды:
. (11. 8)
Обозначим стационарные состояния модели следующим образом: q1 и q3 – устойчивые, а q2 – неустойчивое стационарное состояние. Рассмотрим поведение бистабильной среды при наложении на нее внешнего возбуждения. Предположим, что стационарное состояние q1 является более устойчивым, чем состояние q3, тогда подверженные внешнему воздействию элементы среды будут стремиться к состоянию q1 и потянут за собой своих соседей - по среде пройдёт волна перехода q3 → q1, которая называется волной переключения.
|
|
|
Рассмотрим распространение волны вдоль оси х. В уравнении заменим переменную t на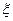 
:
, (11. 9)
где с – скорость распространения волны переключения, t – время. Тогда 
. Введём граничные условия:
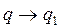при 
; 
при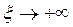 
, (11. 10)
что означает, что сначала вся система была в состоянии q3, а в конце перешла в состояние q1, которое устойчивее. Уравнение среды в новых переменных запишется так:
. (11. 11)
Введем потенциал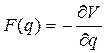 
, тогда уравнение среды примет вид:
. (11. 12)
Полученное уравнение по форме совпадает с уравнением движения частицы в потенциальном поле V с вязким трением, пропорциональным скорости (роль которой играет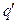 
). Переведём обозначения на язык механики: D (коэффициент диффузии) – это «масса частицы», с (скорость волны переключения) – «динамическая вязкость», q – «пространственная координата», 
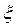- время. Адекватность динамических уравнений, как известно, свидетельствует о подобии явлений - поэтому, проследив, как будет двигаться частица, попробуем сделать выводы о поведении бистабильной среды.
Если «вязкое трение» отсутствует, т. е. с=0, то величина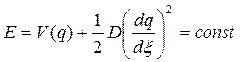 
- энергия «частицы». Тогда «частица», получив жёсткое возбуждение, достаточное для преодоления потенциального барьера при q2, падая вниз, проскочит яму при q1 и поднимется вверх по склону горы на уровень, соответствующий запасу её энергии, а затем станет двигаться обратно и опять перескочит потенциальный барьер, вернувшись в положение q3 (см. рис. 11. 2):
Рис. 11. 2. К вопросу определения скорости волны переключения.
Если значение вязкости с велико, то частица под действием возбуждения не сможет проскочить потенциальный барьер и перейти в состояние q1 – она застрянет на склоне. Существует единственное значение вязкости с = с0 , при котором частица, получив жёсткое возбуждение, попадает из q3 в состояние q1: при с0 потеря энергии на трение должна быть в точности равна разности потенциала в точках q1 и q3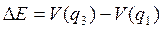 
. Это значение с0 и определяет скорость волны переключения.
|
|
|
Скорость волны переключения с0 определяется только характеристиками среды, а не величиной внешнего воздействия. С уменьшением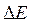 
с0 убывает, при 
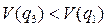волна пойдёт в другую сторону. Для произвольного вида функции F(q) нет аналитических способов расчета с0. В частном случае, если F(q) представляет собой полином третьей степени, имеем:
, (11. 13)
Отсюда можно получить точное решение:
. (11. 14)
Рассмотрим поведение активной среды в зависимости от начальных условий. Допустим, что в начальный момент времени среда неоднородна, т. е. часть ее находится в состоянии q1, а часть – в q3. Проследим за эволюцией начального состояния, при этом рассмотрим несколько основных случаев.
1. Начальное состояние среды незначительно отклонено от одного из стационарных состояний (см. рис. 11. 3а). Тогда со временем вся среда переходит в ближайшее стационарное состояние.
2. Часть среды находится в состоянии q1, часть – в состоянии q3. Граница будет двигаться так, чтобы во всей системе установилось более устойчивое стационарное состояние (рис. 11. 3б).
3. Любое другое начальное состояние можно получить как комбинацию случаев 1 и 2 (рис. 11. 3в). Всегда в среде происходит релаксация к одному из стационарных состояний. Поэтому две столкнувшиеся волны гасят друг друга – аннигилируют.
4. Малые возмущения среды стремятся рассосаться (рис. 11. 3г), т. к. нахождение среды в одном стационарном состоянии оказывается энергетически более выгодным. Если начальное состояние не соответствовало наиболее устойчивому (т. е. состоянию с более глубоким минимумом потенциала), то, создав достаточно большое возмущение, её можно перевести в последнее.
Рис. 11. 3. Эволюция начальных распределений в бистабильной среде: а – случай 1, б – случай 2, в – случай 3, г – случай 4 (образование критического зародыша).
При анализе поведения среды обнаруживается аналогия с фазовыми превращениями первого рода. Пусть фазы соответствуют состояниям q1 и q3. Фаза q1 отвечает абсолютному минимуму потенциала - при фазовых превращениях 1 рода это означает, что фаза стабильна. Состояние q3 отвечает локальному минимуму потенциала и соответствует метастабильной фазе в равновесии. Образовавшийся зародыш стабильной фазы достаточно большого размера начинает расти и дает начало двум разбегающимся волнам переключения (фронт кристаллизации, например), после чего вся среда переходит в стабильное состояние. Критический размер зародыша определяется, как и в кинетике фазовых превращений, из баланса двух факторов: уменьшения (термодинамического) потенциала системы при переходе в более устойчивое состояние и наличия возмущения, которое повышает потенциал. Если оба состояния равнозначны (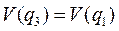 
), то возможно стационарное сосуществование двух фаз с плоским переходным слоем (аналог границы зерна в поликристалле), несмотря на то, что это повышает энергию системы. Когда размер системы много больше толщины переходного слоя, система может разбиться на произвольное количество областей – доменов, соответствующих разным фазам.
|
|
|
|
|
|
