 |
Лекция 1: «основные понятия теории вероятностей»
|
|
|
|
ЛЕКЦИЯ 1: «ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ»
Понятие о случайном событии
Опыт, эксперимент, наблюдение явления называется испытанием.
Примеры: бросание монеты, бросание игральной кости.
Результат, исход испытания называется событием.
Примеры: выпадение герба, появление того или иного числа очков на брошенной игральной кости.
Для обозначения событий используют большие буквы латинского алфавита: A, B, C и т. д.
Определение 1. Два события называются совместимыми, если появление одного из них не исключает появление другого в одном и том же испытании.
Пример. Испытание – однократное бросание игральной кости. Событие A – появление четырёх очков, событие B - появление чётного числа очков.
Определение 2. Два события называют несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.
Пример. Испытание – однократное бросание монеты. Событие A – выпадение герба, событие B - выпадение цифры.
Определение 3. Два события A и B называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.
Событие, противоположное событию A, обозначают через 
.
Определение 4. Событие называют достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти.
Определение 5. Событие называют случайным, если оно объективно может наступить или не наступить в данном испытании.
Пример. Событие A – выпадение шести очков при бросании игральной кости – случайное.
Можно ли как-то измерить возможность появления некоторого случайного события?
|
|
|
Классическое определение вероятности
Определение 1. Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится, хотя бы одно из них.
Примеры: попадание в цель или промах при одном выстреле; выпадение герба и выпадение цифры при одном бросании монеты.
Определение 2. События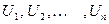 
, образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.
Определение 3. Событие A называют благоприятствующим событию B, если наступление события A влечёт за собой наступление события B.
Определение 4 (классическое определение вероятности). Вероятностью 
события A называют отношение 
числа элементарных событий, благоприятствующих событию A, к числу всех элементарных событий, т. е. 
.
Пример. Найти вероятность того, что при бросании игральной кости выпадет чётное число очков (событие A).
n=6; m=3;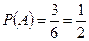 
.
Из классического определения вероятности вытекают следующие её свойства:
1. Вероятность достоверного события равна единице.
Доказательство: m=n, тогда 
.
2. Вероятность невозможного события равна нулю.
Доказательство: m=0, тогда 
.
3. Вероятность случайного события есть положительное число, заключённое между нулём и единицей.
Доказательство: 
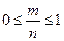
Основные формулы комбинаторики
Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определённого типа можно составить из данных предметов (элементов).
Определение 1. Размещениями из n различных элементов по m элементов (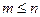 
) называют комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.
Пример. Из трёх элементов a, b, c можно составить следующие размещения по два элемента: ab, ac, bc, ba, ca, cb.
Число различных размещений из n элементов по m элементов определяется по формуле:
|
|
|
.
Определение 2. Перестановками из n различных элементов называют размещения из этих n элементов по n.
Перестановки можно считать частным случаем размещений при m=n. Тогда число всех перестановок из n элементов вычисляется по формуле:
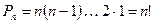
Определение 3. Сочетаниями из n различных элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые отличаются хотя бы одним элементом.
Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов.
Число сочетаний из n элементов по m элементов вычисляется по формуле:
или
.
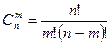Пример. В лабораторной клетке содержат трёх белых и трёх коричневых мышей. Найдите число способов выбора двух мышей, если они могут быть любого цвета.
m=2, n=6, тогда 
.
|
|
|
