 |
Теорема сложения вероятностей совместимых событий
|
|
|
|
Теорема сложения вероятностей совместимых событий
Теорема. Вероятность суммы двух совместимых событий A и B равна сумме вероятностей этих событий минус вероятность их произведения:
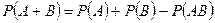(3)
Доказательство:
Используем классическое определение вероятности. Пусть в данном испытании число всех элементарных событий равно n, событию A благоприятствуют k элементарных событий, событию B – l элементарных событий, одновременно событиям A и B – m элементарных событий. Отсюда событию A+B благоприятствуют k+l-m элементарных событий. Тогда по определению вероятности:
; 
; 
; 
.
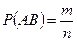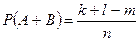Следовательно,
.
Теорема доказана.
Замечание. Если события A и B несовместимы, то AB - невозможное событие, отсюда 
. Мы получаем формулу 
.
Пример. В посевах пшеницы на делянке имеется 95% здоровых растений. Выбирают два растения. Определить вероятность того, что хотя бы одно среди них окажется здоровым.
Событие A – первое растение здоровое;
событие B – второе растение здоровое;
событие A+B – хотя бы одно растение здоровое.
Тогда
.
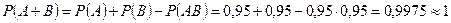Формула полной вероятности
Теорема. Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместимых событий 
, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:
. (3)
Формула (3) называется формулой полной вероятности.
Доказательство: самостоятельно
Примеры.
1) Имеются три одинаковых по виду ящика. В первом находятся две белые мыши и одна серая, во втором – три белые и одна серая, в третьем – две белые мыши и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь?
|
|
|
Событие 
- выбор первого ящика;
событие 
- выбор второго ящика;
событие 
- выбор третьего ящика;
событие A - извлечение белой мыши.
Так как все ящики одинаковы, то
; 
; 
; 
.
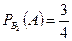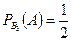По формуле (3) получаем:
.
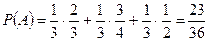2) Для приёма зачёта преподаватель заготовил 50 задач: 20 задач по дифференциальному исчислению, 30 задач по интегральному исчислению. Для сдачи зачёта студент должен решить первую же доставшуюся ему наугад задачу. Какова вероятность для студента сдать зачёт, если он умеет решать 18 задач по дифференциальному исчислению и 15 задач по интегральному исчислению.
Событие - получена задача по дифференциальному исчислению;
событие - получена задача по интегральному исчислению;
событие A – задача решена.
Тогда
; 
; 
; 
.
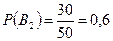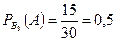Применяем формулу (3):
.
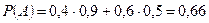ЛЕКЦИЯ 2: «ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ»
Случайные величины: дискретные и непрерывные
Определение 1. Случайной величиной называют переменную величину, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.
Пример. Число очков, выпавших при однократном бросании игральной кости, есть случайная величина, она может принять одно из значений 1, 2, 3, 4, 5, 6.
Случайные величины обозначаются прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z.
Определение 2. Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется дискретной случайной величиной.
Определение 3. Случайная величина, которая может принимать все значения из некоторого числового промежутка, называется непрерывной случайной величиной.
|
|
|
