 |
Свойства вероятности. Теорема сложения вероятностей несовместимых событий. Теорема умножения вероятностей
|
|
|
|
Свойства вероятности
Теорема сложения вероятностей несовместимых событий
Определение 1. Суммой событий A и B называется событие A+B, состоящее в наступлении, по крайней мере, одного из событий A или B.
Аналогично, суммой конечного числа событий 
называют событие 
, состоящее в наступлении хотя бы одного из событий 
.
Определение 2. Произведением событий A и B называется событие C=AB, состоящее в том, что в результате испытания произошло и событие A, и событие B.
Аналогично, произведением конечного числа событий называют событие 
, состоящее в том, что в результате испытания произошли все указанные события.
Теорема. Вероятность суммы двух несовместимых событий A и B равна сумме вероятностей этих событий.
Доказательство:
Используем классическое определение вероятности. Пусть в данном испытании число всех элементарных событий равно n, событию A благоприятствуют k элементарных событий, событию B – l элементарных событий, событию A+B – k+l элементарных событий (так как события A и B - несовместимые). Тогда по определению вероятности:
; 
; 
.
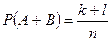Следовательно,
.
Теорема доказана.
Следствие. Сумма вероятностей противоположных событий A и 
равна единице:
.
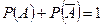Доказательство:
События A и несовместимы. Применим доказанную теорему:
,
но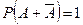 
, так как событие 
является достоверным (одно из событий A или произойдёт). Тогда .
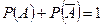Пример. На клумбе растут 20 красных, 30 синих и 40 белых астр. Какова вероятность сорвать в темноте окрашенную астру, если срывают одну астру?
A - событие, состоящее в том, что срывают красную астру;
B - событие, состоящее в том, что срывают синюю астру.
; 
; 
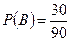Теорема умножения вероятностей
|
|
|
Определение 1. Два события A и B называют независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называют зависимыми.
Определение 2. Пусть A и B – зависимые события. Условной вероятностью 
события B называют вероятность события B, найденную в предположении, что событие A уже наступило.
Если события A и B независимы, то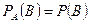 
.
Теорема 1. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие уже наступило:
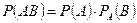(1)
Доказательство: самостоятельно
Пример. В ящике находятся 2 белых и 2 чёрных шара. Вынули два шара (вынутый в первом испытании шар не возвращается обратно в ящик). Какова вероятность вынуть первый и второй раз белые шары?
A - событие, состоящее в том, что первый раз вынули белый шар;
B - событие, состоящее в том, что второй раз вынули белый шар, при условии, что в первый раз тоже был вынут белый шар
По теореме 1 получаем: 
.
Теорема 2. Вероятность произведения двух независимых событий A и B равна произведению вероятностей этих событий:
(2)
Доказательство: Так как A и B – независимые события, то 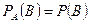и из формулы (1) получается формула (2).
Пример. Вероятность выживания одного организма в течение 20 мин p=0, 7. В пробирке с благоприятными для существования этих организмов условиями находятся только что родившиеся два организма. Какова вероятность того, что через 20 мин они будут живы?
Событие A – первый организм жив через 20 мин;
событие B – второй организм жив через 20 мин.
Будем считать, что события A и B независимы. Тогда вероятность события AB, состоящего в том, что оба организма живы, вычисляется по формуле (2):
|
|
|
.
|
|
|
