 |
Лекция 6: «элементы математической статистики»
|
|
|
|
ЛЕКЦИЯ 6: «ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ»
Генеральная и выборочная дисперсии.
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят такую характеристику, как генеральная дисперсия.
Определение. Генеральной дисперсией  называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней
называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней  .
.
Если все значения  признака генеральной совокупности объёма N различны, то
признака генеральной совокупности объёма N различны, то
 . (7)
. (7)
Если же значения признака  имеют соответственно частоты
имеют соответственно частоты  , причём
, причём  , то
, то
 . (8)
. (8)
Пример. Генеральная совокупность задана таблицей распределения:
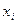
| ||||

|
Найти генеральную дисперсию.
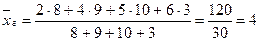 ,
,
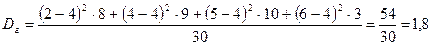 .
.
Определение. Генеральным средним квадратическим отклонением (стандартом) называется  .
.
Дисперсия признака X, рассматриваемого, как случайная величина, равна  .
.
Тогда  ,
, 

 .
.
Величина  называется средней квадратической ошибкой.
называется средней квадратической ошибкой.
Определение. Выборочной дисперсией  называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней
называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней 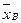 .
.
Если все значения  признака выборки объёма n различны, то
признака выборки объёма n различны, то
 . (9)
. (9)
Если же значения  признака имеют соответственно частоты
признака имеют соответственно частоты  , причём
, причём 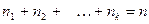 , то
, то
 . (10)
. (10)
Пример. Выборочная совокупность задана таблицей распределения:
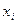
| ||||
|
Найти выборочную дисперсию.
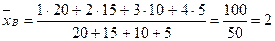 ;
;
 .
.
Выборочным средним квадратическим отклонением (стандартом) называется квадратный корень из выборочной дисперсии:  .
.
|
|
|
Пример. 
Будем считать значения  признака различными.
признака различными.
Выборочную дисперсию, рассматриваемую как случайную величину, будем обозначать 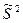 :
:
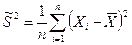 .
.
Теорема. Математическое ожидание выборочной дисперсии равно  , т. е.
, т. е.  .
.
Оценки параметров распределения.
Одной из задач статистики является оценка параметров распределения случайной величины X по данным выборки. При этом считают, что генеральная совокупность бесконечна, чтобы переходить к пределу при  , где n – объём выборки. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров.
, где n – объём выборки. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров. 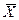 является оценкой генеральной средней
является оценкой генеральной средней  , а
, а 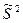 – оценкой генеральной дисперсии
– оценкой генеральной дисперсии  .
.
Обозначим через 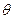 оцениваемый параметр, через
оцениваемый параметр, через 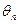 – оценку этого параметра (
– оценку этого параметра ( 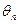 составлена из
составлена из 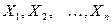 ). Для того чтобы оценка давала хорошее приближение, она должна быть несмещённой и состоятельной.
). Для того чтобы оценка давала хорошее приближение, она должна быть несмещённой и состоятельной.
Определение. Несмещённой называют оценку 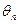 , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру 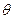 , т. е.
, т. е. 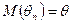 , в противном случае оценка называется смещённой.
, в противном случае оценка называется смещённой.
Оценка 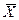 – несмещённая оценка генеральной средней, т. к.
– несмещённая оценка генеральной средней, т. к.  .
.
Оценка 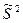 – смешённая оценка генеральной дисперсии, т. к.
– смешённая оценка генеральной дисперсии, т. к.  .
.
Наряду с выборочной дисперсией 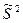 рассматривают исправленную дисперсию
рассматривают исправленную дисперсию 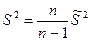 , которая также является оценкой генеральной дисперсии.
, которая также является оценкой генеральной дисперсии.
 .
.
Таким образом, оценка  является несмещённой оценкой генеральной дисперсии.
является несмещённой оценкой генеральной дисперсии.
Для  получаем:
получаем:
 .
.
Таким образом,
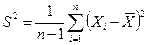 . (11)
. (11)
В качестве приближённого неизвестного параметра берут несмещённые оценки, для того чтобы не сделать систематические ошибки в сторону завышения или занижения.
Определение. Состоятельной называют такую оценку 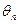 параметра
параметра 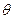 , что для любого наперёд заданного числа
, что для любого наперёд заданного числа  вероятность
вероятность 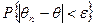 при
при  стремится к единице; то есть при достаточно больших n можно с вероятностью, близкой к единице, утверждать, что оценка
стремится к единице; то есть при достаточно больших n можно с вероятностью, близкой к единице, утверждать, что оценка 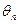 отличается от оцениваемого параметра
отличается от оцениваемого параметра 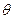 меньше, чем на
меньше, чем на 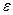 .
.
|
|
|
Несмещённая оценка 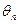 будет состоятельной, если её дисперсия стремится к нулю при
будет состоятельной, если её дисперсия стремится к нулю при  :
:  .
.
Несмещённые оценки 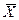 и
и  являются состоятельными. Оценки
являются состоятельными. Оценки  и
и 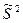 на практике не различаются при
на практике не различаются при 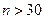 .
.
Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно корню квадратному из исправленной дисперсии:
 . (12)
. (12)
Через  и S будем обозначать левые части формул (11) и (12), заменяя случайные величины
и S будем обозначать левые части формул (11) и (12), заменяя случайные величины 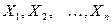 их реализациями
их реализациями  , а
, а 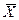 – выборочной средней
– выборочной средней 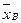 .
.
Если 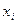 – большие числа, то для облегчения вычислений используют формулу:
– большие числа, то для облегчения вычислений используют формулу:
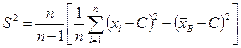 ,
,
где C – ложный нуль.
Пример. С плодового дерева случайным образом отобрано 10 плодов. Их вес  (в граммах) записан в первой колонке таблицы. Найти
(в граммах) записан в первой колонке таблицы. Найти 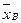 и S.
и S.
Пусть C=250.
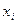
| 
| 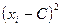
|
| -25 -30 -5 -39 -16 -20 -19 | ||
| -72 |
 ;
;
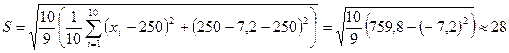 ;
;
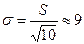 .
.
Оценка генеральной средней веса плода равна 243 г со средней квадратической ошибкой 9 г.
Оценка генерального среднего квадратического отклонения веса плода равна 28 г.
|
|
|


