 |
Закон нормального (гауссовского) распределения.
|
|
|
|
Закон нормального (гауссовского) распределения.
Закон распределения вероятностей непрерывной случайной величины X называется нормальным, если её плотность вероятности определяется формулой:
, (1)
где 
.
График функции f(x) (кривая Гаусса) имеет следующий вид (точка максимума 
), причём его максимальная ордината 
убывает с возрастанием значения 
(кривая «сжимается» к оси OX) и возрастает с убыванием значения (кривая «растягивается» в положительном направлении оси OY). Изменение значения параметра a (при неизменном значении ) не влияет на форму кривой.
Нормальное распределение с параметрами 
называется нормированным. Функция плотности вероятности для такого распределения имеет вид:
.
Для этой функции составлена таблица её значений для положительных значений x (функция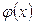 
чётная). График 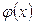имеет следующий вид:
Эту кривую называют единичной нормальной кривой. Она играет роль стандарта, т. е. любые собранные в статистических исследованиях данные стремятся преобразовать так, чтобы кривая их распределения была максимально близка к этой стандартной кривой.
Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу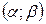 
равна:
.
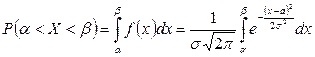Сделаем замену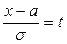 
, тогда 
, получаем:
. (2)
Интеграл 
не вычисляется в элементарных функциях, поэтому для вычисления интеграла (2) вводится функция
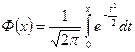, (3)
которая называется функцией Лапласа или интегралом вероятностей. Для функции Лапласа составлена таблица её значений для положительных значений x.
|
|
|
Свойства функции Лапласа.
1. 
.
Доказательство: 
.
2. Ф(x) – нечётная функция, т. е. Ф(-x)=-Ф(x).
Доказательство:
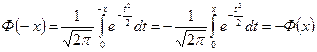(замена t=-z, dt=-dz).
3. Функция Ф(x) монотонно возрастает.
Из формул (2) и (3) следует, что вероятность того, что случайная величина X примет значение из интервала 
равна:
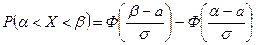. (4)
Пример. Случайная величина X распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 0 и 2. Найти вероятность того, что X примет значение, принадлежащее интервалу (-2; 3).
. По формуле (4) получаем:
.
Часто требуется вычислить вероятность того, что отклонение нормально распределённой случайной величины X от её математического ожидания по абсолютной величине меньше заданного положительного числа 
, т. е. найти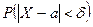 
. По формуле (4) получаем:
.
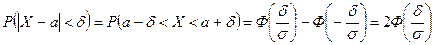Таким образом,
. (5)
Пример. Пусть случайная величина X распределена по нормальному закону с параметрами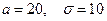 
. Найти 
.
Нормальное распределение вероятностей имеет в теории вероятностей большое значение. В частности, закон распределения суммы достаточно большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, близок к нормальному распределению. Этот факт получил название центральной предельной теоремы.
ЛЕКЦИЯ 5: «ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ»
Математическая статистика разрабатывает научно обоснованные методы сбора статистических данных.
Генеральная совокупность и выборка
Пусть требуется изучить множество однородных объектов (это множество называется статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Если сплошное обследование, т. е. изучение каждого объекта, невозможно, то из всей совокупности выбирают для изучения часть объектов. Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.
|
|
|
Число объектов генеральной совокупности и выборки называется соответственно объёмом генеральной совокупности и объёмом выборки.
Пример. Плоды одного дерева (200 шт. ) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 – объём генеральной совокупности, 10 - объём выборки.
Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике чаще встречается бесповторная выборка.
Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, т. е. выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т. е. выбор производится случайно.
|
|
|
