Статистическое распределение выборки. Полигон. Гистограмма.

Статистическое распределение выборки. Полигон. Гистограмма.

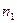Пусть из генеральной совокупности извлечена выборка, причём значение  наблюдалось  раз, значение  -  раз, значение  -  раз и 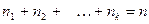 – объём выборки. Наблюдаемые значения  называются вариантами, а последовательность вариант, записанная в возрастающем порядке, - вариационным рядом. Числа наблюдений  называются частотами, а их отношения к объёму выборки  – относительными частотами. Тогда .

Статистическим распределением выборки называется перечень вариант и соответствующих им частот (или относительных частот).

Статистическое распределение можно задать в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал. Для графического изображения статистического распределения используются полигоны и гистограммы.

Для построения полигона на оси OX откладывают значения вариант 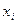, на оси OY – значения частот  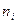(относительных частот ).

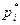Пример. Постройте полигон для распределения:

 

Варианта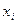
Относительная частота	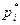0, 4	0, 2	0, 3	0, 1

 

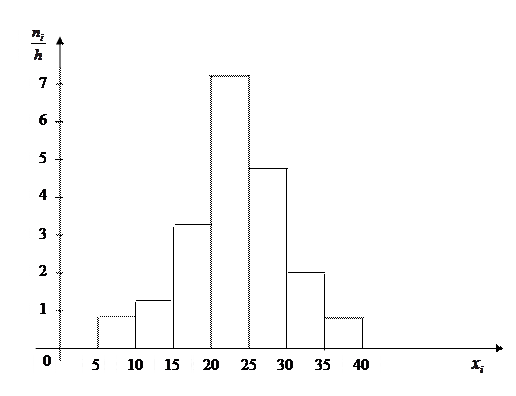
В случае непрерывного распределения признака строят гистограммы. Интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и для каждого частичного интервала находят сумму частот вариант 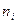, попавших в i–ый интервал. Затем на этих интервалах, как на основаниях, строят прямоугольники с высотами  (или , где n - объём выборки). Площадь i-го частичного прямоугольника равна  (или ). Следовательно, площадь гистограммы равна сумме всех частот, т. е. объёму выборки (или относительных частот, т. е. единице).

Пример. Изобразить гистограмму непрерывного распределения объёма n=100, приведённого в таблице.

 

Частичный интервал h	Сумма частот вариант частичного интервала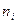
5-10 10-15 15-20 20-25 25-30 30-35 35-40		0, 8 1, 2 3, 2 7, 2 4, 8 2, 0 0, 8

 

 

Оценки параметров генеральной совокупности по её выборке.

Извлечение объекта из генеральной совокупности можно рассматривать как испытание, количественный признак X – как случайную величину. Опытные значения  признака X можно рассматривать как значения разных случайных величин 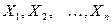 с тем же распределением, что и X. Тогда

.

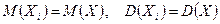Значения  называются реализациями случайных величин .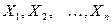

Пусть изучается дискретная генеральная совокупность объёма N относительно количественного признака X.

Определение. Генеральной средней 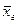 (или a) называется среднее арифметическое значений признака генеральной совокупности.

Если все значения  признака генеральной совокупности объёма N различны, то

.                                     (1)

Если же значения признака  имеют соответственно частоты , причём , то

.                       (2)

или

.

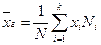Пусть все значения  различны. Так как каждый объект может быть извлечён с одной и той же вероятностью , то .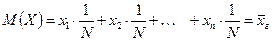

Таким образом,

  .                                                       (3)

Формула (3) справедлива, если значения  имеют соответственно частоты , а также в случае непрерывного распределения признака X.

Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка объёма n.

Определение. Выборочной средней 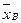 называется среднее арифметическое значений признака выборочной совокупности.

Если все значения  признака выборки объёма n различны, то

.                                    (4)

Если же значения признака  имеют соответственно частоты , причём 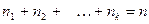, то

                             (5)

или

.

Пример. Выборочным путём были получены следующие данные о массе 20 морских свинок при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28, 27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найти выборочную среднюю .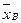

По формуле (5):

.

Если 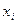 – большие числа, то используют формулу:

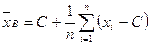.                                           (6)

При этом константу C (так называемый ложный нуль) берут такой, чтобы значения  были наибольшими и число C – целым.

Пример. Имеется выборка:

          

         

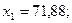
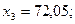
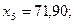
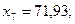
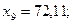
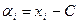Пусть , тогда значения  равны:

          

         

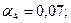
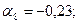
Получаем сумму 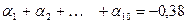, тогда , .

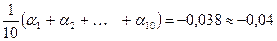Всевозможные выборочные средние есть значения случайной величины:

,

которая называется выборочной средней случайной величиной.

.

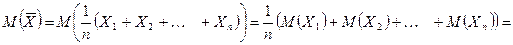
Таким образом, математическое ожидание выборочной средней совпадает с генеральной средней: .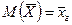

Дисперсия выборочной средней равна .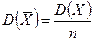

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: