Законы распределения дискретных случайных величин

Законы распределения дискретных случайных величин

Дискретная величина X считается заданной, если перечислены все её возможные значения, а также вероятности, с которыми величина X может принять эти значения. Указанный перечень возможных значений и их вероятностей называют законом распределения дискретной случайной величины. Обычно он задаётся с помощью таблицы:

 

X
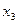
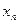
p

 

Так как в результате испытания величина X всегда примет одно из значений , то .

Пример. Пусть случайная величина X – число очков, выпавших при бросании игральной кости. Найти закон распределения случайной величины X.

 

X
p	1/6	1/6	1/6	1/6	1/6	1/6

 

Математическое ожидание и дисперсия дискретной случайной величины

Определение 1. Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятности этих значений.

Если случайная величина характеризуется конечным рядом распределения

 

X
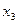
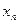
p

 

то математическое ожидание 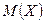 определяется по формуле

;

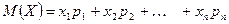т. е.

.

Так как , то

.

Таким образом, 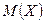 является взвешенным средним арифметическим значений случайной величины  при весах .

Если , то

,

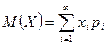при условии, что сумма этого ряда конечна.

Пример. Найти математическое ожидание случайной величины X, зная закон её распределения.

 

X
p	0, 3	0, 1	0, 6

 

Свойства математического ожидания.

1.

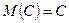
2.

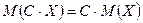
3.

4.

5.

Пример. Независимые случайные величины X и Y заданы следующими законами распределения:

 

X
p	0, 1	0, 3	0, 6

 

Y
p	0, 8	0, 2

 

Найти математическое ожидание случайной величины XY.

,

,

.

Определение 2. Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

.

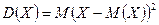Пример. Найти дисперсию случайной величины X, которая задана следующим законом распределения:

 

X
p	0, 3	0, 5	0, 2

 

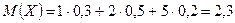
Дисперсия случайной величины есть мера рассеяния её значений около её математического ожидания.

Свойства дисперсии.

1.

2.

3.

4.

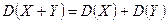
Определение 3. Средним квадратическим отклонением  случайной величины X называется корень квадратный из её дисперсии:

.

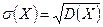Пример. Случайная величина X – число очков, выпавших при однократном бросании игральной кости. Определить .

Закон распределения случайной величины X задан таблицей:

 

X
p	1/6	1/6	1/6	1/6	1/6	1/6

 

Находим математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X:

;

;

.

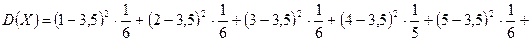
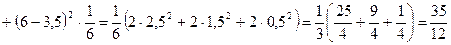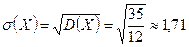Введение среднего квадратического отклонения объясняется тем, что дисперсия измеряется в квадратных единицах относительно размерности самой случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, используется среднее квадратическое отклонение.

 

ЛЕКЦИЯ 3: «НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ»

Интегральная функция распределения

Пусть X - непрерывная случайная величина с возможными значениями из интервала (a; b) и x – действительное число.

Определение. Интегральной функцией распределения (или функцией распределения) непрерывной случайной величины X называется функция F(x), равная вероятности того, что X принимает значение, меньшее x:

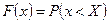.                                                       (1)

Для дискретных величин функция распределения определяется так же.

Свойства функции распределения.

1. .

2. F(x) – неубывающая функция, т. е. если , то .

Доказательство: Пусть .

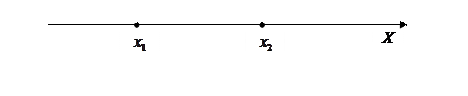
A – событие «X примет значение меньше »;

B – событие «X примет значение меньше »;

C – событие «X примет значение, удовлетворяющее условию ».

Тогда A=B+C, где B и C – несовместны, т. е. P(A)=P(B)+P(C). Таким образом, .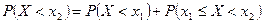

Отсюда .

Так как 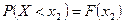, , то 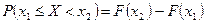. Поскольку , получаем 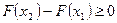, т. е. , что и требовалось доказать.

3. Вероятность попадания случайной величины X в полуинтервал  равна разности между значениями функции распределения в правом и левом концах интервала :

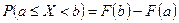.                                    (2)

Пример. Случайная величина X задана функцией распределения:

Найти вероятность того, что в результате испытания X примет значение из полуинтервала .

4. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:

.

5. Вероятности попадания непрерывной случайной величины в интервал, отрезок и полуинтервал с одними и теми же концами одинаковы:

.

6. Если возможные значения случайной величины X принадлежат интервалу (a; b), то:

1) F(x)=0 при ;

2) F(x)=1 при .

Следствие. Если возможные значения непрерывной случайной величины X расположены на всей числовой оси, то ; .

 

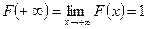⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: